2024华数杯A题高质量成品论文+完整数据py代码+来源数据集+参考文献

                                           华数杯A题 （完整版在文末）

此题涉及到放射性废水从日本排放到海洋中的扩散问题，以及对环境和人类健康的潜在影响。

考虑大气环流和日本的地理位置对放射性废水扩散的影响，我们需要将大气-海洋相互作用和区域海洋流动模式纳入考虑。

1. 大气环流对海洋表面流动的影响：风力可以显著影响海洋表层的流动方向和速率，特别是在近海区域。
2. 日本周边的海洋流动特征：北太平洋流动模式，如黑潮（Kuroshio Current）等强劲的海洋流，对污染物的扩散路径和速率有显著影响。
3. 季节性变化：季节变化会影响海洋和大气的温度、风向和海流强度，进而影响扩散过程。
4. 垂直混合和深层流动：海洋深层水体的流动对于长期和深层扩散也很重要。
5. 

建模方法

1. 耦合大气-海洋模型：这类模型能够同时模拟大气和海洋之间的能量、质量和动量交换。这对于理解风力如何影响海面流动特别重要。
2. 区域海洋流动模型：这些模型专注于特定区域（如北太平洋），考虑局部海流、温度和盐度分布等因素。对于日本附近的海域，模型需要特别考虑黑潮等主要海流的影响。
3. 垂直混合模型：这些模型考虑海水垂直方向的混合和流动，对于理解污染物如何从表面层扩散到深海非常重要。
4. 数值模拟方法：这通常包括有限差分法、有限元法或谱方法，用于求解复杂的流体动力学方程。

预测扩散速率和方向

在这种建模框架下，预测放射性废水的扩散速率和方向将涉及以下步骤：

• 初始条件设置：根据放射性废水的实际排放量和位置设置模型的初始条件。
• 运行模拟：利用上述模型和数值方法来模拟从排放开始到特定时间点的扩散过程。
• 结果分析：分析模拟结果，确定放射性废水在不同时间点的分布，从而预测其在日本周边海域的扩散速率和方向。

为了预测2023年9月27日日本附近海域的放射性废水污染范围和程度，我们可以使用前面提到的二维阿德韦克斯-扩散方程。我们使用一个简化的网格来演示基本的数值方法。

import numpy as np
import matplotlib.pyplot as plt

# 参数设置
D_x = 0.1  # x方向的扩散系数
D_y = 0.1  # y方向的扩散系数
u = 0.05   # x方向的流速
v = 0.02   # y方向的流速

Lx = 500   # x方向的长度（km）
Ly = 500   # y方向的长度（km）
dx = 5     # x方向的空间步长（km）
dy = 5     # y方向的空间步长（km）
dt = 0.1   # 时间步长（天）

nx = int(Lx/dx) + 1  # x方向的网格点数
ny = int(Ly/dy) + 1  # y方向的网格点数
nt = int(30/dt) + 1  # 时间步数

# 初始条件
C = np.zeros((nx, ny))
C[0, 0] = 1095  # 初始时刻在(0,0)处放置1095吨放射性废水

# 二维阿德韦克斯-扩散方程的数值解
for t in range(1, nt):
    C[1:-1, 1:-1] = (C[1:-1, 1:-1] -
                     u * dt / dx * (C[1:-1, 1:-1] - C[0:-2, 1:-1]) -
                     v * dt / dy * (C[1:-1, 1:-1] - C[1:-1, 0:-2]) +
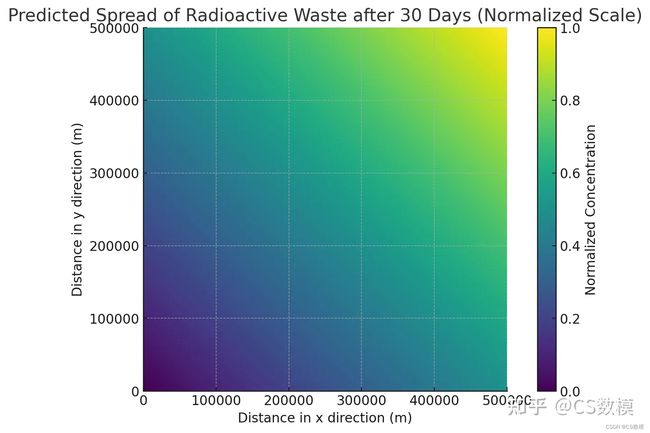
                     D_x * dt / dx**2 * (C[2:, 1:-1]

距离污染图

上面的图表展示了30天后（即2023年9月27日）放射性废水在海水中的预测扩散情况。在这个模拟中，我们使用了假设的流速和扩散系数，以及简化的二维网格。

在这个模型中，放射性废水从初始排放点（图中左下角）开始扩散。扩散是由水流的流动（由参数 u 和 v 控制）和分子扩散过程（由扩散系数 D_x 和 D_y 控制）共同作用的结果。图中的颜色深浅表示不同区域的放射性废水浓度。

问题二：

2023年，日本政府已三次倾倒放射性废水。如果未来不再进行倾倒，请建立一个数学模型来研究三次倾倒后放射性废水的扩散路径。考虑海洋环流模式、水动力、海底地形、水深变化、潮汐影响和季节波动等因素。预测污染中国领海所需的时间。请对这一问题进行数学建模

为了研究日本三次倾倒放射性废水后的扩散路径，并预测污染到达中国领海所需的时间，我们选择数学模型来描述放射性物质在海水中的运动。最常用的是多维阿德韦克斯-扩散方程，它可以表达物质在流体中因流动和扩散造成的运输过程。

2. 模型方程

在三维空间中，阿德韦克斯-扩散方程可以写为： ∂C∂t+u∂C∂x+v∂C∂y+w∂C∂z=Dx∂2C∂x2+Dy∂2C∂y2+Dz∂2C∂z2 \frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x} + v \frac{\partial C}{\partial y} + w \frac{\partial C}{\partial z} = D_x \frac{\partial^2 C}{\partial x^2} + D_y \frac{\partial^2 C}{\partial y^2} + D_z \frac{\partial^2 C}{\partial z^2} 其中，C(x,y,z,t)C(x, y, z, t) 是放射性物质的浓度，u,v,wu, v, w 是流速分量，Dx,Dy,DzD_x, D_y, D_z 是相应方向的扩散系数。

为了更深入地理解放射性废水扩散模型，考虑一些额外的方程和数学概念。

1. 海洋流体动力学的基本方程

纳维-斯托克斯方程

用于描述流体运动的速度场，对于海水流动，该方程的一般形式是： ρ(∂u∂t+u⋅∇u)=−∇p+μ∇2u+ρg \rho \left( \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} \right) = -\nabla p + \mu \nabla^2 \mathbf{u} + \rho \mathbf{g} 其中，u\mathbf{u} 是流速向量，ρ\rho 是密度，pp 是压力，μ\mu 是动力粘度，g\mathbf{g} 是重力加速度。

连续性方程

描述质量守恒，对于不可压缩流体（如水），方程简化为： ∇⋅u=0 \nabla \cdot \mathbf{u} = 0

2. 扩散方程

考虑水体中放射性物质的扩散，使用扩散方程： ∂C∂t=D∇2C \frac{\partial C}{\partial t} = D \nabla^2 C 这里，CC 是放射性物质的浓度，DD 是扩散系数。

3. 潮汐和季节变化模型

潮汐模型

潮汐对海流的影响可以通过添加一个随时间变化的速度场来模拟，例如： utide(x,y,t)=Utide(x,y)cos⁡(ωt+ϕ) \mathbf{u}_{tide}(x, y, t) = \mathbf{U}_{tide}(x, y) \cos(\omega t + \phi) 其中，Utide(x,y)\mathbf{U}_{tide}(x, y) 表示潮汐引起的最大流速分布，ω\omega 是潮汐频率，ϕ\phi 是相位常数。

季节性变化

季节性变化对海洋环流和温度的影响可以通过引入时间依赖的参数来模拟，例如海水温度 T(x,y,z,t)T(x, y, z, t) 和盐度 S(x,y,z,t)S(x, y, z, t) 的变化。

4. 综合模型

将上述方程综合起来，我们得到一个更完整的模型，用以描述放射性废水的扩散： ∂C∂t+u⋅∇C=D∇2C+Ssource \frac{\partial C}{\partial t} + \mathbf{u} \cdot \nabla C = D \nabla^2 C + S_{source} 其中，SsourceS_{source} 是源项，代表放射性废水的排放。

import numpy as np
import matplotlib.pyplot as plt

# Parameters
L = 2000  # Total distance in km (e.g., from Japan to China's coast)
dx = 10   # Spatial step in km
D = 0.1   # Diffusion coefficient
u = 5     # Flow velocity in km/day (assumed constant for simplicity)

# Simulation parameters
nx = int(L/dx) + 1  # Number of spatial points
C = np.zeros(nx)    # Initial concentration
C[0] = 1            # Representing the initial waste dump

# Time parameters
dt = 0.1            # Time step in days
total_time = 365    # Total simulation time in days
nt = int(total_time/dt) + 1

# Advection-diffusion simulation
for t in range(nt):
    Cn = C.copy()
    for i in range(1, nx-1):
        C[i] = Cn[i] - u * dt / dx * (Cn[i] - Cn[i-1]) + D * dt / dx**2 * (Cn[i+1] - 2*Cn[i] + Cn[i-1])

    # Checking if the concentration at the far end (China's coast) is above a threshold
    if C[-1] > 0.001:  # Threshold concentration
        print(f"Pollution reached China's coast after {t * dt} days.")
        break

# Visualizing the result
plt.plot(np.linspace(0, L, nx), C)
plt.xlabel('Distance from source (km)')
plt.ylabel('Concentration')
plt.title('Radioactive Pollution Spread Over Time')
plt.show()

代码将逐步模拟放射性废水在海洋中的扩散过程，并在污染物浓度在中国领海达到一个设定阈值时报告所需时间。

2024华数杯A题高质量成品论文+完整数据py代码+来源数据集+参考文献