数据结构---二叉树

一、引言

1.二叉树产生的背景

在许多实际问题中，数据之间存在层次关系。例如，组织架构、文件系统、编译器语法分析等场景都需要表示层次结构。二叉树作为一种特殊的树结构，能够清晰地表达这种层次关系。最直观的就是我们电脑上的文件夹的层次结构。

---

2.二叉树的基本概念

定义：二叉树是n个（n>0）节点的有限集合。每个节点最多只能有两个子节点，分为左子节点和右子节点，且有左右之分，其次序不能任意颠倒。

---

3.二叉树需要掌握的基本概念

• 根节点：二叉树的顶层节点称为根节点。
• 叶子节点：仅有一个子节点的节点称为叶子节点，也称为终端节点。
• 子树：从根节点到某个节点之间的部分称为子树。二叉树中的子树有左右之分。
• 度：一个节点的子节点数称为该节点的度。二叉树中，度为0的节点称为叶子节点，度为1的节点称为单分支节点，度为2的节点称为双分支节点。

---

4.二叉树的分类

• 满二叉树：所有叶子节点都存在的二叉树，具有最多的节点数。
• 完全二叉树：除了最后一层外，其他层的节点数都达到了最大值，且最后一层的节点都连续集中在左侧的二叉树。
• 非完全二叉树：不符合满二叉树或完全二叉树条件的二叉树。
• 平衡二叉树（AVL树）：每个节点的左右子树的高度相差不超过1，从而保证了树的高度相对平衡。

---

二、树的多种定义方式

1.存孩子指针

struct TreeNode
{
    int data ;
    struct TreeNode* child1;
    struct TreeNode* child2;
    ...
}

2.左孩子右兄弟表示法

typedef int TDataType;
struct Node
{
    struct Node* firstChild1;  //第一个孩子的结点
    struct Node* pNextBrother; //指向其下一个兄弟结点
    TDatatype data;//结点中的数据域
}

上述定义方式如下图所示：

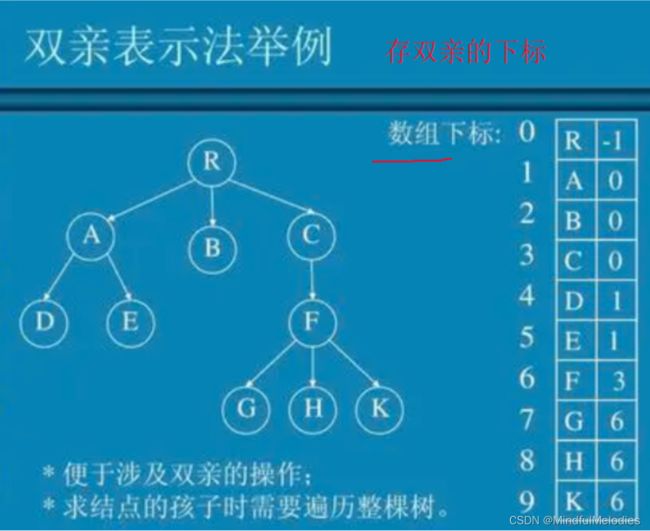
3.双亲表示法

注：孩子内存双亲下标

4.二叉树的定义方式

由于二叉树的孩子树不超过两个，所以可以直接存根的两个孩子的节点的指针。
定义如下：

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

三、二叉树的遍历

注：由于二叉树是不断向下生根，所以这里使用分治算法。
生活中常见的分治算法：学校中统计人数，校长分配到各个院的院长，院长分配到各个系的系长，各个系的系长分配到各个班的班主任，最后分配到各个寝室的寝室长，进行统计。
分治算法：分而治之，将一个大问题拆分为若干个小问题，然后将小问题再拆分为若干个小问题，直到小问题不可拆分为止。

1.二叉树的前序

顾名思义，就是先访问根，再左节点，再右节点
用分治算法处理：

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

2.二叉树的中序

顺序：左节点->根->右节点

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

3.二叉树的后续

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

对于普通二叉树来说讨论其增删查改是没有意义的，所以接下来讨论其节点个数和叶子节点的个数

四、二叉树的节点个数以及二叉树的层序遍历

1.二叉树的节点个数

对于以上算法，最好的方法就是递归

int TreeSize(BTNode* root) 
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

以上算法可以优化为：

int TreeSize(BTNode* root) 
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

2.二叉树的叶子结点个数

由上述节点个数很容易可以得出：

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if(root->left==NULL&&root->right==NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

3.二叉树的层序遍历

对于层序遍历来说不能使用递归，层序遍历只能用非递归方式来遍历。
对于层序遍历需要用到前面的队列的知识。
因为队列是先进先出，所以每存一个节点就出将这个节点取出来并展开成左子树节点和右子树节点存在队列后面，以此类推，一直到NULL最后就不用拆了。

用代码把上图表述出来就是如下：

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root != NULL)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		if (front->left != NULL)
		{
			QueuePush(&q, front->left);
		}
		if (front->right != NULL)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestory(&q);
}

---

五、总结

当然二叉树的知识远不止这些，二叉树相对于前面的栈队列还有链表和顺序表来说难度有较大的提升。