DoubleEnsemble:基于样本重加权和特征选择的金融数据分析方法
现代机器学习模型(如深度神经网络和梯度提升决策树)由于其提取复杂非线性模式的优越能力,在金融市场预测中越来越受欢迎。然而,由于金融数据集的信噪比非常低,并且是非平稳的,复杂的模型往往很容易过拟合。此外,随着各种机器学习和数据挖掘工具在量化交易中的应用越来越广泛,许多交易公司已经提取了越来越多的特征(也称为因子factors)。因此,如何自动选择有效特征成为一个迫在眉睫的问题。为了解决这些问题,作者提出了DoubleEnsemble,这是一个基于样本重新加权和基于shuffling特征选择的集成框架。具体来说,我们基于训练动态识别关键样本,并通过shuffling每个特征的消融影响来引出关键特征。该模型适用于广泛的基础模型,能够提取复杂的模式,同时缓解金融市场预测的过拟合问题。我们使用DNN和GBDT作为baseline,进行了广泛的实验,包括加密货币和股票交易的价格预测。实验结果表明,与几种基线方法相比,DoubleEnsemble实现了优越的性能。
来自:DoubleEnsemble: A New Ensemble Method Basedon Sample Reweighting and Feature Selection forFinancial Data Analysis
目录
- 背景概述
- 相关工作
-
- 集成模型
- 样本重加权
- 特征选择
- 金融数据去噪
- 方法
-
- 样本重加权
- 基于混洗的特征选择
- 实验-股票交易
-
- 实验设置
- 评价指标
- 实验结果
背景概述
众所周知,金融市场难以预测。首先,困难来自众所周知的有效市场理论,该理论认为股价反映的所有信息,不可能完全超过整个市场。其次,由于有大量噪声交易和影响市场运行的隐藏因素(比如政策变化和突发新闻)的存在,金融数据具有高度的噪声。
多因子模型是一种流行的资产定价和市场预测模型。该模型基于多个特征(或因子)对资产进行定价或预测市场走势,如公司规模(firm size)、收益率(earnings’ yield)、杠杆率(leverage)和账面市值比(book-to-market ratio)。线性模型一直是多因子模型的标准算法,但在发现复杂模式方面有很大的局限性。最近,非线性机器学习模型(如GBDT或DNN)变得流行。然而,这些复杂的非线性模型容易过拟合,并且对噪声样本敏感。
为了给模型提供更多信息,量化交易者或研究人员通常会创建数百甚至数千个特征(也称为因子)。因此,选择不仅具有信息性而且与其他特征不相关的特征是至关重要的。对于线性模型(如线性回归),我们可以选择相关性低的特征来缓解多重共线性问题。但是,对于高噪声的财务数据,如何有效地选择特征尚不清楚。
为了解决上述问题,作者提出了一种新的金融数据预测集成框架DoubleEnsemble。该框架在集合中逐个构建子模型,其中每个子模型都使用重加权的样本和精心选择的特征进行训练。广泛的模型可作为子模型,如线性回归模型、GBDT和DNN。
在实验中,作者将DoubleEnsemble应用于两个金融市场,即加密货币交易所OKEx和证券交易所中国A股市场(China’s A-share market)。这两个市场具有不同的交易规则和市场参与者,因此在这两个交易市场的历史数据中存在不同类型的噪声和模式。此外,作者使用DoubleEnsemble来构建预测模型,以不同的频率(从几秒到几周)进行交易。实验表明,DoubleEnsemble在这两个市场上都取得了优异的性能。
相关工作
集成模型
集成是增强模型鲁棒性的有效方法。集成模型的关键是构建良好的和多样化的子模型。构建子模型的方法可以分为两类。在第一类中,可以单独构建不同的模型,例如bagging。另一类是基于先前构建的子模型的性能构建子模型,如boosting。通过这类方法建立的模型具有更好的预测精度,但容易过拟合训练数据中的噪声。
样本重加权
对模型训练的样本进行加权在一些计算机视觉应用中被证明是有效的。在为训练样本分配权重时,boosting和denoising的目标之间存在冲突。boosting会增加困难样本的权重,模型首先拟合简单样本,然后拟合困难样本。在金融市场预测中,这也可以被解释为在利用以前的模式时获得另一种新模式。另一方面,为了构建对异常值和噪声样本具有鲁棒性的集合,应该减少这些噪声样本的权重。然而,我们很难区分困难样本和异常样本。因此,在进行boosting学习的同时,减少噪声样本的权重是一项挑战。
特征选择
通常,金融市场预测的特征是手动选择的。然而,当特征数量增加时,需要实现特征选择的自动化。(Advances in financial machine learning)介绍了金融机器学习的几个特征重要性度量。然而现有方法没有研究如何结合样本重加权来选择特征以获得更好的性能。
金融数据去噪
降噪是从低信噪比的金融数据中提取信息的关键。作者重点讨论了模型的训练。除了重加权样本去噪外,过去的研究一般是设计特定的损失函数去噪。降噪可以从信号处理的角度进行(例如,在提取特征之前对原始序列数据进行滤波)。
方法
作者提出了DoubleEnsemble,这是一个具有两个关键组件的模型:基于学习轨迹的样本重加权和基于混洗的特征选择。
训练数据包含特征矩阵 X X X和标签 y y y,其中, X = [ x 1 , . . . , x N ] T ∈ R N × F X=[x_{1},...,x_{N}]^{T}\in R^{N\times F} X=[x1,...,xN]T∈RN×F, x i x_{i} xi是 X X X的第 i i i个样本,另外, y = [ y 1 , . . . , y N ] y=[y_{1},...,y_{N}] y=[y1,...,yN]。依次构建 K K K个子模型 M 1 , . . . , M K M_{1},...,M_{K} M1,...,MK。在构建第 k k k个子模型后,当前的集成模型 M ‾ k ( ⋅ ) = 1 k ∑ i = 1 k M i ( ⋅ ) \overline{M}^{k}(\cdot)=\frac{1}{k}\sum_{i=1}^{k}M^{i}(\cdot) Mk(⋅)=k1∑i=1kMi(⋅)为前 k k k个模型的简单平均。
每个子模型不仅基于训练数据 ( X , y ) (X,y) (X,y),也基于一组选定的特征 f ⊆ F f\subseteq F f⊆F和样本权重 w = ( w 1 , . . . , w N ) w=(w_{1},...,w_{N}) w=(w1,...,wN)进行训练。对于第一个子模型,使用所有特征和相等的权重。对于随后的子模型,分别使用基于学习轨迹的样本重加权(SR,sample reweighting)和基于混洗的特征选择(FS)来确定权重和选择特征。
在介绍SR和FS的细节之前,首先介绍这两个过程的输入。对于SR,我们检索前一个子模型训练期间的loss曲线和当前集成模型的loss值。假设前一个子模型训练 T T T次迭代。我们使用 C ∈ R N × T C\in R^{N\times T} C∈RN×T来表示loss曲线,其中元素 c i , t c_{i,t} ci,t表示在前一个子模型的训练中第 t t t次迭代后第 i i i个样本上的误差。对于神经网络,迭代指的是一个训练epoch,而对于GBDT,我们在迭代中构造一个新的树。然后,我们使用 L ∈ R N × 1 L\in R^{N\times 1} L∈RN×1表示损失值,元素 l i l_{i} li是当前集成模型在第 i i i个样本上的误差(比如 M ‾ k ( x i ) \overline{M}^{k}(x_{i}) Mk(xi)和 y i y_{i} yi的误差)。对于FS,我们直接提供训练数据和当前集成作为输入。
样本重加权
在这个过程中,首先计算每个样本的 h h h值,然后根据 h h h值将所有样本划分为 B B B个bins,再将相同的权重分配给同一个bin中的样本。
h h h值的计算基于前一个子模型的 C C C和当前集成模型的 L L L。对于鲁棒性,首先对 C C C和 L L L进行标准化( R N × d → [ 0 , 1 ] N × d R^{N\times d}\rightarrow [0,1]^{N\times d} RN×d→[0,1]N×d)。比如,如果 X i j X_{ij} Xij大于 X X X第 j j j列元素的90%,则 n o r m ( X ) i j = 0.9 norm(X)_{ij}=0.9 norm(X)ij=0.9,为了表示在训练过程中样本的丢失是否得到改善,作者比较了它在训练开始和结束时的损失。作者使用 C s t a r t , C e n d ∈ R N × 1 C_{start},C_{end}\in R^{N\times 1} Cstart,Cend∈RN×1分别表示训练开始和结束时所有样本的损失。具体地说,它们分别是前10%列和后10%列的平均值。比如,如果对每个子模型训练 T = 100 T=100 T=100个迭代次数, C s t a r t C_{start} Cstart中的每个元素为前10次迭代中样本的平均归一化损失。然后,我们计算所有样本的 h h h值:
SR算法如下: h = α 1 ( − L ) + α 2 n o r m ( C e n d C s t a r t ) (1) h=\alpha_{1}(-L)+\alpha_{2} norm(\frac{C_{end}}{C_{start}})\tag{1} h=α1(−L)+α2norm(CstartCend)(1)其中, h ∈ R N × 1 h\in R^{N\times 1} h∈RN×1。为了避免权值极值,进一步根据 h h h值将样本划分为 B B B个bins,并为同一个bin中的样本分配相同的权重。假设第 i i i个样本被分成第2个bin。该样本的权重分配如下: w i = 1 γ k < h > b i + 0.1 (2) w_{i}=\frac{1}{\gamma^{k}
基于混洗的特征选择
作者在DoubleEnsemble中用基于混洗的FS训练下一个子模型,与SR相似,首先计算每个特征的 g g g值,然后根据 g g g值将所有特征划分为 D D D个bins,然后,从不同的bin中随机选择不同采样比例的特征。
特征的 g g g值度量了该特征对当前集成的贡献(即特征重要性)。为了计算特征的 g g g值,作者对该特征的值进行混洗,并比混洗前后的损失(算法3中的第5-7行)。当特征的消除(通过混洗实现)显著增加样本上的损失时,特征的 g g g值较大,这表明该特征对当前集成很重要。为了提高 g g g值的鲁棒性,作者根据 g g g值将所有特征划分为 D D D个bins,并随机从具有不同采样比率的不同bin中选择特征(算法3中的第8-12行)。采样比率是预设的,并且对于具有较大 g g g值的bin,该比率较大。最后,将所有随机选择的特征拼接并返回。
这样设计的原因如下:为了估计一个特征对模型的贡献,我们想要比较该特征不存在时的性能。一种自然但代价高昂的方法是消除特征,重新训练,然后重新评估模型。我们不是训练一个新的模型,而是对数据集进行扰动以消除特征的贡献,并比较使用扰动数据集和使用原始数据集的模型的性能。由于不需要重新训练模型,该方案在计算上更有效。
实验-股票交易
作者使用 K = 6 K = 6 K=6个子模型。在SR过程中,使用 α 1 = α 2 = 1 α_1 = α_2 = 1 α1=α2=1, B = 10 B = 10 B=10个bins。在FS过程中,使用 D = 5 D = 5 D=5个bins,样本比例为 ( 0.8 ; 0.7 ; 0.6 ; 0.5 ; 0.4 ) (0.8;0.7;0.6;0.5;0.4) (0.8;0.7;0.6;0.5;0.4)。
在这个实验中,作者训练股票市场的预测器,并根据预测结果进行股票交易。实验以中国A股市场为基础,该市场有3000多只股票在交易。每个样本对应一个股票的一个交易日。
实验设置
作者在两种不同的环境下进行实验。在第一个设置中(用DAILY表示),我们在每个交易日收盘时做多predictor建议的前20只股票,然后在下一个交易日收盘时卖出这些股票。该预测基于182个特征,这些特征值是在该交易日收盘前3分钟计算出来的(这些特征可能包括当天的价格变动、交易量、以及其他市场指标等)。在第二个设置中(用WEEKLY表示),在每个交易日收盘后,根据历史市场信息计算254个特征并进行预测。在接下来的一个交易日,我们以开盘价做多预测建议的前10只股票,并持有5个交易日。此后,我们在第五个交易日开盘后卖出这些股票。在这种情况下,我们大部分时间持有50只股票。两种情况下的特征是为不同频率的预测而设计的,由不同的交易公司创建。因此,它们具有完全不同的基本性质。由于实验的特征较多,作者在MLP模型中使用了三个神经元较多的隐藏层(分别为256、128和64个神经元),在GBM模型中使用了250棵树。
做多是指“先买入,后卖出”,做空是指“先卖出,再买入”。在金融市场中,做多指看好股票、外汇或期货等未来的上涨前景而进行买入持有等待上涨获利。例如,如果你认为某股票的市场价格会涨到150元,你可以用100元买入该股票,等到市场价格涨到150元时再卖出,就可以赚50元了。
作者按照如下所述的滚动方案对模型运行回测:每周重新训练模型,并在每次训练模型时使用最近500个交易日(即大约最近两年)的特征(所以结果图中的曲线会呈现整体上升的情况,就像loss总是不断被降低)。两种设置的交易期限为2017年1月至2019年11月。对于交易细节,不包括在3个月内上市的股票,然后以同等权重做多排名前N的股票。
评价指标
Ann.Ret:我们用对冲后的年化收益来衡量由模型构建的投资组合所获得的收益超过市场的多少。我们把每天的资金分成两部分,分别用来买股票和对冲市场。为了对冲市场,我们做空相应的股指期货。
"做空相应的股指期货"是金融交易中的一个策略,指的是出于预期股指将下跌的判断(预期股指通常指的是市场参与者对股票市场未来运动趋势的预期),通过卖出股指期货合约来获取利润的行为。在这个策略中,交易者不持有股指期货合约的实际持仓,而是先卖出合约,希望在未来以更低的价格买入同等数量的合约来平仓,从而赚取卖高买低的差价。
这种做空策略通常用于对冲风险或投机。例如,如果投资者持有一篮子股票,且这篮子股票与某股指表现高度相关,他们可能会通过做空这个股指的期货来对冲持仓股票的下跌风险。如果股市下跌,股票持仓的价值可能会减少,但做空股指期货的部分将会获得收益,从而减少总体损失。
Sharpe:夏普比率是股票投资最常用的指标之一,它反映了风险调整后的盈利能力。
MDD:最大损失是投资组合从峰值到低谷的最大相对损失。MDD是一个特定时期内下行风险的指示器。MDD与投资者的最大承受能力有关,需要保持尽可能低的价格。
IC/IR:信息系数IC和信息比IR表示预测的质量。这里的IC是mean IC。
实验结果
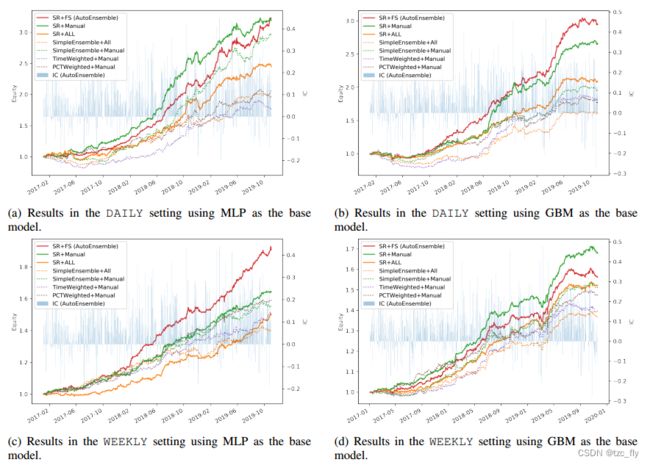
图中绘制了模型在不同设置下的对冲权益曲线。表中列出了回测结果的性能度量。

- 不同模型在不同设置下的对冲权益曲线。背景中的蓝色条表示总体预测的IC。
图中展示了四组实验。四组实验分别在不同的设定(DAILY和WEEKLY)和不同的基模型(MLP和GBM)下进行。图中曲线为不同模型对冲后的权益曲线,背景中的蓝条表示SR+FS模型在每个交易日的IC。交易日的IC是该交易日模型输出的连续信号与实际未来收益之间的Spearman秩相关系数。权益曲线(equity)反映了top检索样本的预测精度,IC反映了所有样本的预测精度。
可以看到SR+FS(红线)的性能优于SR+ALL(橙色线)。这表明FS的有效性。但是,FS过程的自动特征选择不如手动选择特征,这是一个相当强的基准。因此,作者将发现一种可与人工选择相媲美或更好的端到端自动特征选择方法作为未来的研究方向。
此外,观察到具有SR过程的模型比没有SR过程的模型(即SimpleEnsemble)获得了更好的性能。这可以通过比较SR+Manual模型(绿色实线)和SimpleEnsemble+Manual模型(绿色虚线)或者比较SR+ALL模型(橙色实线)和SimpleEnsemble+ALL(橙色虚线)来观察。这说明SR可以通过对关键样本的关注来提高性能。
基础模型(如MLP)的输入为股票在特定日期下的因子值,如技术指标、基本面指标等。输出则依赖于实验的具体目标,可能是股票未来一段时间的收益率、价格变动或是涨跌趋势的分类