代码随想录算法训练营第35天 | 860.柠檬水找零 406.根据身高重建队列 452.用最少数量的箭引爆气球
柠檬水找零

局部最优:收到20元时优先找零10元+5元,不够再找零3个5元,因为5元可以找零20和10,更有用。全局最优:完成所有的找零。
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int five = 0, ten = 0;
for(int i = 0; i < bills.size(); i++){
if(bills[i] == 5){
five++;
}
else if(bills[i] == 10){
if(five){
ten++;
five--;
}
else return false;
}
else{
if(ten && five){
ten--;
five--;
}
else if(five >= 3){
five -= 3;
}
else return false;
}
}
return true;
}
};
根据身高重建队列

贪心问题中如果不遇到保持原有顺序或者原来顺序有意义的情况,一般都是需要对输入重新排序的,这样方便设计贪心策略。这道题也是一开始需要对原数组进行排序。
原数组有两个维度,从分发糖果那道题中我们可以获得经验,这种有两个维度的问题,可以先满足一个维度的条件,再考虑另外一个维度。我们把原数组按身高从大到小排序,保证前面的人肯定是比后面的人高,身高相同则k小的站在前面。可以设计贪心策略为:
优先按身高高的人的k值插入结果数组中,这样一定可以满足他前面始终有k个人的身高都大于等于下标k位置的人。
class Solution{
static bool cmp(vector<int>& a, vector<int>& b){
if(a[0] != b[0]) return a[0] > b[0];
else return a[1] < b[1]; // 优先比较身高,身高从大到小,身高相同则将k小的放前面
}
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people){
sort(people.begin(), people.end(), cmp);
vector<vector<int>> que;
for(int i = 0; i < people.size(); i++){
int index = people[i][1];
que.insert(que.begin() + index, people[i]);
}
return que;
}
};
这个算法的时间复杂度表面看应该是 O(nlogn + n^2),因为insert的时间复杂度为 O(n)。但是在C++底层实现中,vector构建的动态数组之所以能随意添加元素,是因为它的扩容机制。当插入元素导致当前的数组容量不够时,会开辟一个是原来容量二倍的新数组空间,将现在的数组拷贝过去,再将原数组从内存中释放。这样其实时间复杂度变成了 O(n^2 + t * n),t 就是拷贝的次数。
所以我们可以考虑用链表实现insert的过程。
class Solution{
static bool cmp(vector<int>& a, vector<int>& b){
if(a[0] != b[0]) return a[0] > b[0];
else return a[1] < b[1];
}
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people){
sort(people.begin(), people.end(), cmp);
list<vector<int>> que;
for(int i = 0; i < people.size(); i++){
int index = people[i][1];
std::list<vector<int>>::iterator it = que.begin();
while(index--){
it++;
}
que.insert(it, people[i]);
}
return vector<vector<int>>(que.begin(), que.end());
}
};
用最少数量的箭引爆气球

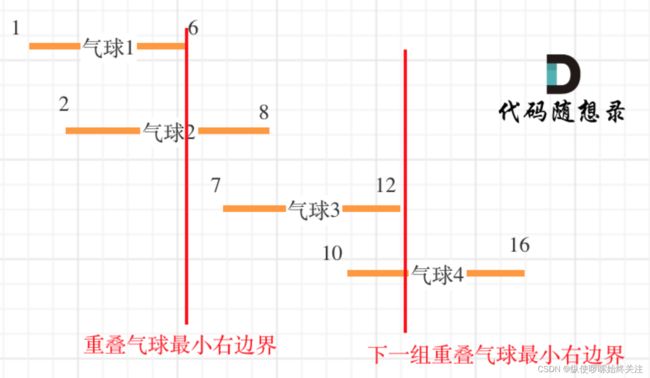
如果气球重叠了,那么重叠的这一组气球的最小右边界位置一定需要一支箭,才能一箭射爆这一组重叠气球。这个逻辑有不同的实现方式,我们可以先对气球的右边界从小到大进行排序,每次射击优先射击最小的右边界,同时跳过已经被射爆的气球。
class Solution{
static bool cmp(vector<int>& a, vector<int>& b){
return a[1] < b[1];
}
public:
int findMinArrowShots(vector<vector<int>>& points){
sort(points.begin(), points.end(), cmp);
int shot = points[0][1];
int result = 1;
for(int i = 0; i < points.size(); i++){
if(points[i][0] > shot){ // 该气球没被射爆,同时有最小的右边界
shot = points[i][1];
result++;
}
}
return result;
}
};
也可以按气球的左边界排序,通过遍历排序好的气球维护当前重叠气球的最小右边界,一旦出现左边界大于右边界的气球,说明该气球不与上一组气球重叠,另外需要一支箭,以此类推。
class Solution{
static bool cmp(vector<int>& a, vector<int>& b){
return a[0] < b[0];
}
public:
int findMinArrowShots(vector<vector<int>>& points){
sort(points.begin(), points.end(), cmp);
int result = 1; // 有气球至少需要一支箭
for(int i = 1; i < points.size(); i++){
if(points[i][0] > points[i - 1][1]){
result++;
}
else{
points[i][1] = min(points[i - 1][1], points[i][1]); //更新当前的最小右边界
}
}
return result;
}
};