pix2pix图像着色学习记录(pytorch实现)
1、BCELoss
BCELoss(binary_crossentropy)二分类交叉熵损失函数,用于图片多标签分类,n张图片分m类,会得到n*m的矩阵,经过sigmoid把矩阵数值变换到0~1,然后通过如下公式计算得到:
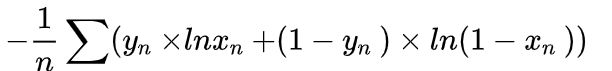
不同分类问题用到的激活函数和损失函数有所不同:
| 分类问题名称 | 输出层使用卷积函数 | 对应的损失函数 |
|---|---|---|
| 二分类 | sigmoid函数 | 二分类交叉熵损失函数 |
| 多分类 | softmax函数 | 多分类交叉熵损失函数 |
| 多标签分类 | sigmoid函数 | 二分类交叉熵损失函数 |
2、nn.ReLU(inplace=True)
inplace=true的意思是进行覆盖运算,如:
nn.ConvTranspose2d(in_features, out_features, 3, stride=2, padding=1, output_padding=1),
nn.InstanceNorm2d(out_features),
nn.ReLU(inplace=True)
即对从上步InstanceNorm2d得到的tensor直接进行修改,这样节约内存,不用多存储其他变量。
3、nn.Conv2d()
class torch.nn.Conv2d(in_channels, out_channels,
kernel_size, stride=1, padding=0,
dilation=1, groups=1, bias=True,
padding_mode='zeros', device=None,
dtype=None)
功能解释:对由多个输入平面组成的输入信号运用二维卷积。
参数解释:
in_channels:指输入的四维张量[N, C, H, W]中的C,即输入图像通道数;
out_channels:指卷积后期望的输出张量的通道数;
kernel_size:卷积核的大小,一般写一个数,如3,代表卷积核大小是3×3,如果卷积核左右大小不一样,则写成元组的形式,如kernel_size=(3, 5);
stride=1:步长,默认为1,卷积核在图像窗口上每次平移的间隔,也可以为一个元组;
padding=0:填充操作,默认为0,填充包括上下左右,比如原始图像大小为30×30,padding=1,则填充后,图像大小为32×32;
dilation=1:是否采用空洞卷积,默认为1(不采用),一般采用默认值,先不深究其意思;
groups=1:决定是否采用分组卷积,默认为1(不分组);
bias=True:默认为True,是否要添加偏置参数作为一个可学习参数;
padding_mode=’zeros‘:padding的模式,默认采用零填充。
卷积操作的一般公式:
H o = ( H i − K + 2 P ) / S + 1 H_o=(H_i-K+2P)/S+1 Ho=(Hi−K+2P)/S+1
其中, H H H也可以替换为 W W W,表示输入/输出的高度和宽度。
4、nn.ConvTranspose2d()
逆卷积,与卷积参数类似。
class torch.nn.ConvTranspose2d(in_channels,
out_channels,kernel_size,
stride=1, padding=0,
output_padding=0, groups=1,
bias=True, dilation=1)
in_channels(int) – 输入信号的通道数
out_channels(int) – 卷积产生的通道数
kerner_size(int or tuple) - 卷积核的大小
stride(int or tuple,optional) - 卷积步长,即要将输入扩大的倍数。
padding(int or tuple, optional) - 输入的每一条边补充0的层数,高宽都增加2*padding
output_padding(int or tuple, optional) - 输出边补充0的层数,高宽都增加padding
groups(int, optional) – 从输入通道到输出通道的阻塞连接数
bias(bool, optional) - 如果bias=True,添加偏置
dilation(int or tuple, optional) – 卷积核元素之间的间距
每条边的输出尺寸的公式如下:
H o u t p u t = ( H i n p u t − 1 ) S − 2 P + K + o u t p u t p a d d i n g H_{output}=(H_{input}-1)S-2P+K+outputpadding Houtput=(Hinput−1)S−2P+K+outputpadding
5、nn.Module()(未深刻理解)
pytorch中对于一般的序贯模型,可以直接调用torch.nn.Sequential类实现,但是对于复杂的模型,比如多输入多输出、多分支模型、跨层连接模型等等,就需要自己来定义。
nn.Module是nn中的一个类,可以用来自定义自己的网络,基本步骤:
(1)自定义一个类,要继承nn.Module类,并一定实现两个函数。__init__构造函数和forward方法,forward是层的逻辑运算函数,也即前向计算函数。
(2)__init__中定义参数。比如Linear层的权重和偏置,Conv2d层的in_channels,out_channels等。
(3)forward函数中实现前向计算。一般是通过torch.nn.functional函数实现,也可以自己定义运算方式,表示__init__中各层的连接关系(顺序等)。
注意一些技巧:
(1)一般把网络中具有可学习参数的层(如全连接层、卷积层等)放在构造函数__init__中。
(2)一般把不具有可学习参数的层(如ReLU)可放在构造函数中,如果不放在__init__中,则在forward方法里面可以使用nn.functional来代替。
(3)forward方法是必须要重写的,它是实现模型的功能,实现各个层之间的连接关系的核心。
(4)一般情况下,我们定义的参数是可以求导的,但是自定义操作如不可导,需要实现backward函数。
参考了:
(1)pytorch教程之nn.Module类详解
(2)pytorch教程之nn.Module类详解——使用Module类来自定义网络层
6、torch.nn.Parameter()
nn.parameter()是将普通的tensor转换为module的可训练的参数,会被加入到parameter()这个迭代器中,成为模型的一部分,会随着模型的训练而变化,而module的非parameter的普通tensor不会加入到parameter()的迭代器中。
7、nn.ReflectionPad2d()
nn.ReflectionPad2d(padding)函数作用:利用输入边界的反射来填充输入张量。
这句话有两个重要的词,“边界”和“反射”,边界是指输入张量的边界,“反射”类似物理中的镜面反射,就是以“边界”为反射面,将输入中的某行某列反射到界外,达到填充的目的。
当padding是一个int型时(如k),表示上下左右都填充相同的k;当padding是一个元组时(如(Left,Right, Top, Bottom)),这时按照元组的要求的那样进行填充。
代码示例:
# padding为int型:填充为1
import torch
import torch.nn as nn
m = nn.ReflectionPad2d(1)
input = torch.arange(9, dtype=torch.float).reshape(1, 1, 3, 3)
print(input)
print(m(input))
输出结果:

可以看出以蓝色框为“反射面”,将输入的
( 1 4 7 ) \begin{pmatrix} 1&\\ 4&\\ 7&\\ \end{pmatrix} ⎝⎛147⎠⎞
反射到外边以完成填充。
# padding为int型:填充为2
import torch
import torch.nn as nn
m = nn.ReflectionPad2d(2)
input = torch.arange(9, dtype=torch.float).reshape(1, 1, 3, 3)
print(input)
print(m(input))
输出结果:
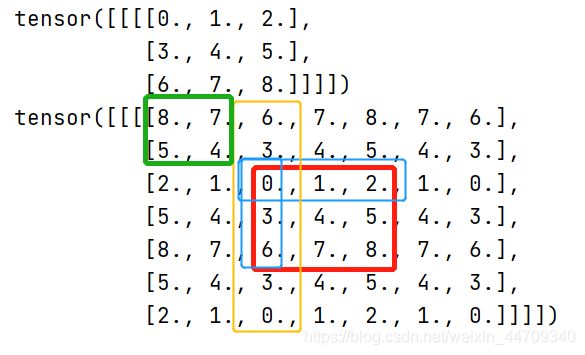
可以看出,上下左右还是以边界为“反射面”进行反射填充,只是四个角(绿色框),是以黄色区域为边界进行反射填充。
#当padding为元组时:(1,1,0,2)意思是左右分别填充为1,上边填充0,下边填充2.
import torch
import torch.nn as nn
m = nn.ReflectionPad2d((1,1,0,2))
input = torch.arange(9, dtype=torch.float).reshape(1,1,3,3)
print(input)
print(m(input))
输出结果:

参考了:
1、图解pytorch padding方法 ReflectionPad2d
8、UNet网络
[⭐推荐⭐]对UNet结合pytorch代码介绍的一篇很不错的博文:
Pytorch深度学习实战教程(二):UNet语义分割网络|Jack Cui
(1)feature map(特征图)
feature map是输入图像经过卷积核卷积运算后得到的结果,表征的是输入图像的一种特征。
层与层之间会有若干个卷积核(kernel),上一层的每个feature map跟卷积核做卷积运算得到下一层的feature map。
当每层有多个feature map时,这几个feature map表示从不同角度对图片进行描述,比如颜色深浅、形状边缘、直线形状等,这几个feature map是不同卷积核卷积得到的结果。
参考了:
1、Feature Map
2、CNN中的feature map
(2)Leaky ReLU
激活函数 R e L U ReLU ReLU是将小于0的c值都置为零,函数图如下:
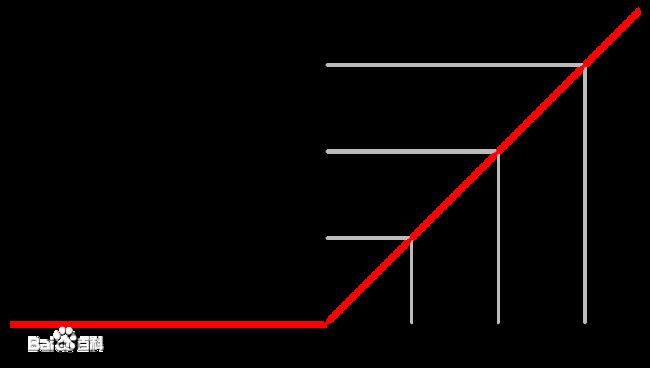
ReLU的效果图如下:
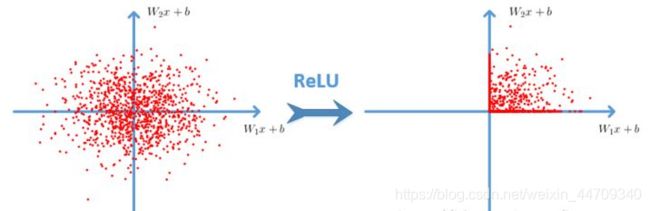
但是使用 R e L U ReLU ReLU容易出现梯度消失的问题。
L e a k y R e L U Leaky ReLU LeakyReLU可以解决这个问题,其表达式如下:
f ( n ) = { α x , x <0 x , x ≥0 f(n)= \begin{cases} αx, & \text {$x$ <0} \\ x, & \text{$x$≥0 } \end{cases} f(n)={αx,x,x <0x≥0
其效果图如下:
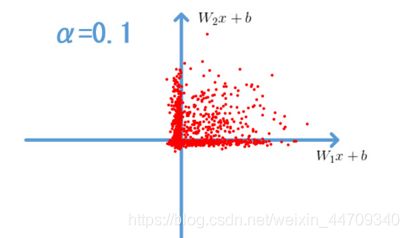
在生成对抗网络GAN中使用的是 L e a k y R e L U Leaky ReLU LeakyReLU而不是 R e L U ReLU ReLU。
参考了:
1、为什么在生成对抗网络(GAN)中,隐藏层中使用leaky relu比relu要好?