三种形式全排列——指数型、排列型、组合型类型题目汇总

题型汇总如下：

一、指数型(子集、组合问题)

1.1 递归实现指数型枚举

与leetcode78.子集是一样的
可以参考这篇链接把里面的题目都做一下，并且这一篇文章用到的子集的思路我觉得在做子集2的时候用剪枝时候的思想可以统一起来，当做模版，并且里面都是for进行遍历，剪枝的时候里面直接把剪枝的条件continue就可以了

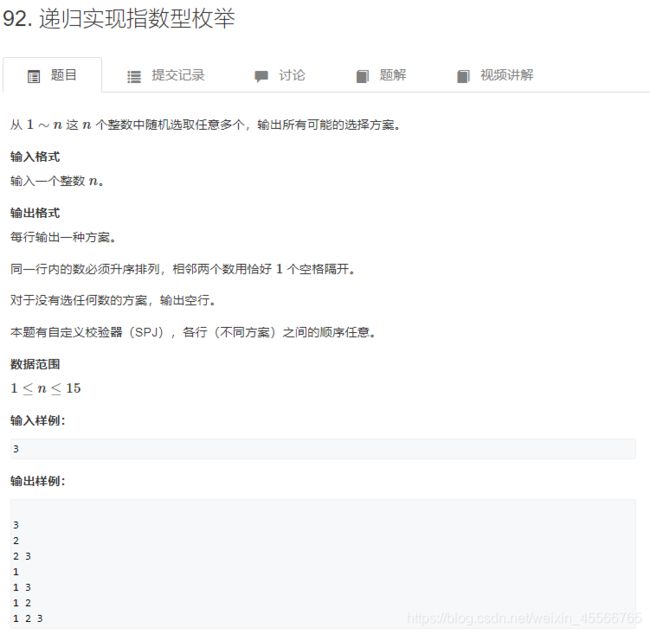
指数型按照升序把所有中方案输出出来

#include

using namespace std;

#define N 20
int n;

int st[N];
int a[N];
void dfs(int u)
{
    if( u == n+1 )
    {
        for(int i = 1; i <=n; i++) //满足三个数的时候
        {
            if(st[i]==1)  //如果我们选了这个数才把他打印出来
                cout << i << " ";
        }
        cout << endl;
        return;
    }
    st[u] = 0; //不选这个数我们置0
    dfs(u+1);
    st[u] = 1; //选这个数我们置1
    dfs(u+1);
}

int main()
{
    cin >> n;
    dfs(1);
    return 0;
}

子集[推荐写法]

这里换一种思路去写上面的问题，反正都是一直往里面添加方案，我们for遍历的时候每次从下一个数开始就可以了，得到的就是所有的方案

class Solution {
public:
    vector<vector<int>> rec;
    vector<int> path;
	vector<vector<int>> subsets(vector<int>& nums) {
		
		dfs(rec, nums, 0, path);
		return rec;
	}

	void dfs(vector<vector<int>>& rec, vector<int> nums, int u, vector<int> path) {
        if(u == nums.size()+1)    //可要可不要
        	return;
		rec.push_back(path);
		for (int i = u; i < nums.size(); i++) {
			path.push_back(nums[i]);
			dfs(rec, nums, i + 1, path);
			path.pop_back();
		}
	}
};

1.2 子集II 这一题可以跟全排列2进行比较，里面的退出剪枝条件是一样的

class Solution {
public:
    vector<vector<int>> rec;
    vector<int> path;
    int st[20] = {0};
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        dfs(0,nums);
        return rec;
    }
    void dfs(int u,vector<int>& nums)
    {
        int n = nums.size();
        if( u == n)
        {
            rec.push_back(path);
            return;
        }
        //不选
        dfs(u+1,nums);

        //选
        if( u > 0 && nums[u] == nums[u-1] && st[u-1] == 0)
            return;
        if( st[u]==0 )
        // if( st[u]==0 && (u==0 || nums[u] != nums[u-1] || st[u-1] == 1))
        {
            st[u] = 1;
            path.push_back(nums[u]);
            
            dfs(u+1,nums);
            path.pop_back();
            st[u] = 0;
        }
    }
};

实现方法二：按照上面子集的方法去写，然后剪枝跟下面的全排列2的方法一样 [推荐写法]

class Solution {
public:
    vector<vector<int>> rec;
    vector<int> path;
    bool st[11] = {0};
	vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(),nums.end());
		dfs(rec, nums, 0,st);
		return rec;
	}

	void dfs(vector<vector<int>>& rec, vector<int> nums, int u,bool st[]) {
        if(u == nums.size()+1)    
            return;
		rec.push_back(path);
		for (int i = u; i < nums.size(); i++) {
            if(i > 0 && nums[i] == nums[i-1] && st[i-1] == 0) //不是第一个数，且不重复的数
                continue;
            st[i] = 1;
			path.push_back(nums[i]);
			dfs(rec, nums, i + 1,st);
            st[i] = 0;
			path.pop_back();
		}
		
	}
};

二、排列型

2.1 94. 递归实现排列型枚举

全排列则需要多加一个for遍历所有的开始情况，而不是选或不选，而是标记状态选没选过。

#include

using namespace std;

int n;
#define N 10
int st[N];
int a[N];
void dfs(int u)
{
    if( u == n + 1)
    {
        for(int i = 1; i <= n; i++)
        {
            cout << a[i] << " ";
        }
        cout << endl;
        return;
    }
    
    for(int i = 1;i <=n;i++) //枚举所有的可能
    {
        if(st[i] == 0)
        {
            a[u] = i;
            st[i] = 1;
            dfs(u+1);
            st[i] = 0;
            
        }
        
    }

}

int main()
{
    cin >> n;
    dfs(1);
    return 0;
}

用vector实现更容易理解 [推荐写法]

#include
#include
using namespace std;

#define N 1000
int n;
vector<int>res;
bool st[N];

void dfs(int u){
    
     if(res.size()==n)
     {
         for(auto a: res)
            cout << a << ' ';
         cout << endl;
         return;
     }
     
     for(int i = 1;i <= n; i++ )
     {
          if(st[i]==0)
          {
              res.push_back(i);
              st[i] = 1;
              dfs(u+1);
              res.pop_back();
              st[i] = 0;
          }
          
     }
}

int main()
{
    cin >> n; 
    dfs(1);
    return 0;
}

2.2 46. 全排列

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    int st[1000] = {0};
    vector<vector<int>> permute(vector<int>& nums) {
        int n = nums.size();
        dfs(1,n,nums);
        return res;
    }
    void dfs(int u,int n,vector<int>& nums)
    {
        if( path.size() == n)
        {
            res.push_back(path);
            return;
        }

        for(int i = 0; i < n;i++)
        {
            if( st[i] == 0)
            {
                st[i] = 1;
                path.push_back(nums[i]);
                dfs(u+1,n,nums);
                st[i] = 0;
                path.pop_back();
            }
        }

    }
};

2.3 全排列2

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    int st[1000] = {0};
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        int n = nums.size();
        if(n==0)
            return res;
        sort(nums.begin(),nums.end());
        dfs(0,n,nums);
        return res;
    }
    void dfs(int u,int n,vector<int>& nums)
    {
        if( path.size() == n)
        {
            res.push_back(path);
            return;
        }

        for(int i = 0; i < n;i++)
        {
            if( i>0 && nums[i] ==  nums[i-1] && st[i-1]==0) //如何筛选重复出现的数字，
            //比如 1 1如果前面 st[i-1] =0,第一个1没有用过，而第二个1就不可以再用了，这样就可以得到筛掉重复出现的数字。
            //如果第一个用了第二个就可以再用一次。
                continue;
            if( st[i] == 0)
            {
                st[i] = 1;
                path.push_back(nums[i]);
                dfs(u+1,n,nums);
                st[i] = 0;
                path.pop_back();
            }
        }

    }
};

2.4 字符串的全排列

2.5 784. 字母大小写全排列

跟子集的写法又有点像了

class Solution {
public:
    vector<string> rec;
    string path;
    vector<string> letterCasePermutation(string s) {
        dfs(0,s);    
        return rec;
    }
    void dfs(int u,string s)
    {
        rec.push_back(s);

        for(int i = u; i < s.size();i++)
        {
            if( s[i] <= 'z' && s[i] >='a')
            {
                s[i] -= 32;
                dfs(i+1,s);
                s[i] += 32;
            }
            else if(  s[i] <= 'Z' && s[i] >='A' )
            {
                s[i] += 32;
                dfs(i+1,s);
                s[i] -= 32;
            }
        }
    }
    
};

三、组合型

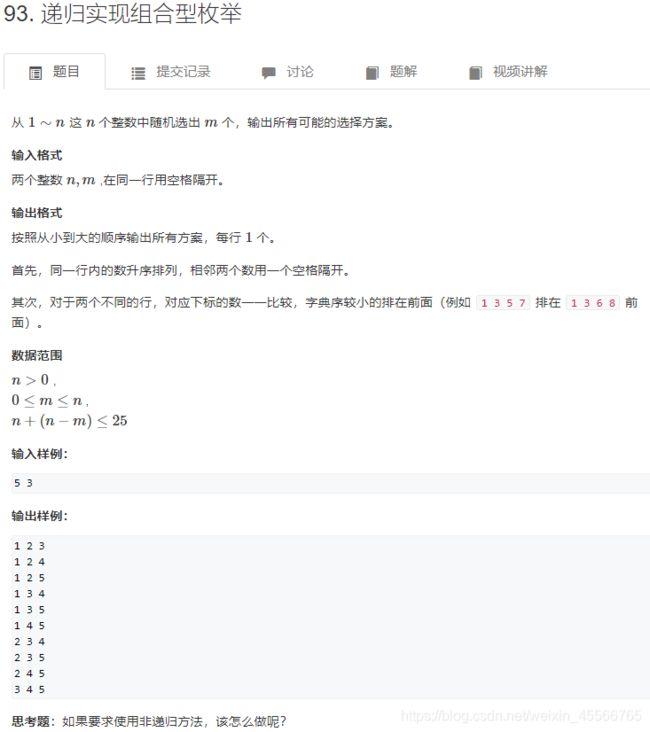
3.1 93. 递归实现组合型枚举

实现思路1：用start索引

#include

using namespace std;

#define N 1000
int n,m;
int st[N];
void dfs(int u, int start)
{                                         //剩余可选的数
    if( u + (n - start) < m ) //已经选的数u + (总数n - 起始的start)
        return;
    if( u == m + 1)
    {
        for(int i =1;i<=m;i++)
        {
            cout << st[i] << " ";
        }
        cout << endl;
        return;
    }
    
    for(int i = start; i <=n; i++)
    {
        st[u] = i;
        dfs(u + 1,i + 1); //下一个开始的点为i+1
        st[u] = 0;
    }
    
}

int main()
{
    cin >> n >> m; 
    dfs(1,1);
    return 0;
}

实现思路二：更容易理解 [推荐写法]

#include
#include
using namespace std;

#define N 1000
int n,m;
vector<int>res;

void dfs(int u){
     if(res.size()==m)
     {
         for(auto a: res)
            cout << a << ' ';
         cout << endl;
         return;
     }
     for(int i = u;i <= n; i++ )
     {
          res.push_back(i);
          dfs(i+1);
          res.pop_back();
     }
}

int main()
{
    cin >> n >> m; 
    dfs(1);
    return 0;
}

3.2 77. 组合

同样的道理，我们开始的时候从u开始，下一次要从for循环里面的i开始，这样才能按照顺序进行打印

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    
    vector<vector<int>> combine(int n, int k) {
        if( n == 0)
            return res;
        dfs(1,n,k);
        return res;
    }

    void dfs(int u,int n,int k)
    {
        if(path.size() == k)
        {
            res.push_back(path);
            return;
        }
        for(int i = u; i <=n;i++)
        {
            path.push_back(i);
            dfs(i+1,n,k);
            path.pop_back();  
        }

    }
};

3.3 39. 组合总和

这也是一个组合问题，并且需要判除重复的情况，注意看dfs下一步的操作，跟上一题组合很像，又跟指数型也很像，避免出现重复方案就定义一个u下一次从u或者u+1开始

class Solution {
public:
    vector<vector<int>> rec;
    vector<int> path;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        dfs(0,candidates,target);
        return rec;
    }
    void dfs(int u, vector<int>& nums, int target)
    { 
         if(target==0) 
         {
              rec.push_back(path);
              return;
         }
         for(int i= u ;i < nums.size();i++) 
         {
            if( nums[i]<=target )
            {
                path.push_back(nums[i]);
                //我们选择数的时候从当前以及当前数的后面的数接着选，避免出现组合情况比如 2 2 3 的时候出现 2 3 2 、3 2 2
                //跟子集、子集II 选择的时候问题很像
                dfs(i,nums,target-nums[i]);
                path.pop_back();
            }
         }
         // 下面的方式去写也可以，我觉得下面这种写法方便理解一点。
         //  for(int i= u ;i < nums.size();i++) 
        //  {
        //     if( nums[i]<=target )
        //     {
        //         path.push_back(nums[i]);
        //        target-=nums[i];
        //         //我们选择数的时候从当前以及当前数的后面的数接着选，避免出现组合情况比如 2 2 3 的时候出现 2 3 2 、3 2 2
        //         //跟子集、子集II 选择的时候问题很像
        //         dfs(i,nums,target); //这里从i开始下一次搜索
        //         path.pop_back();
        //         target+=nums[i];
        //     }
        //  }
    }
};

3.4 40. 组合总和 II

class Solution {
public:
    vector<vector<int>> rec;
    vector<int> path;
    bool st[1000] = {0};
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        dfs(0,candidates,target);
        return rec;
    }
    void dfs(int u,vector<int>& nums,int target)
    {

        if( target == 0)
        {
            rec.push_back(path);
            return;
        }
        for(int i = u ;i < nums.size(); i ++)
        {
            //剪枝去一下重，对于[10,1,2,7,6,1,5]这一个案例 如果没有这一句的话，会有两个[1,7]，因为两个1都会与7组合，所以当前面一个1没有用的时候
            //我们用后面一个1的话就跳过
            if( i >0 && nums[i-1]== nums[i] && st[i-1] == 0)
                continue;
            if( target >= nums[i])
            {

                target -= nums[i];
                st[i] =1;
                path.push_back(nums[i]);
                dfs(i+1,nums,target);
                target += nums[i];
                st[i] =0;
                path.pop_back();
            }
        }

    }
};

3.5 216. 组合总和 III

class Solution {
public:
    vector<vector<int>> rec;
    vector<int> path;
    int sum = 0;
    vector<vector<int>> combinationSum3(int k, int n) {
        int cnt = 0;
        dfs(1,k,n,cnt); //这里我们多加一个cnt变量就可以，记一下dfs的次数
        return rec;
    }
    void dfs(int u,int k,int n,int cnt)
    {   
        if(sum > n) //判断一下特殊情况提前返回 ，和大于了n，或者有了三个数，但是和不是n
            return;
        if( cnt == k && sum != n)
            return;
        if( sum == n &&  cnt == k)
        {
            rec.push_back(path);
            return;
        }

        for(int i = u; i <=9;i++)
        {
            if( sum <= n)
            {
                sum += i;
                path.push_back(i);
                dfs(i+1,k,n,cnt+1);
                sum -= i;
                path.pop_back();
            }
        }
    }
};

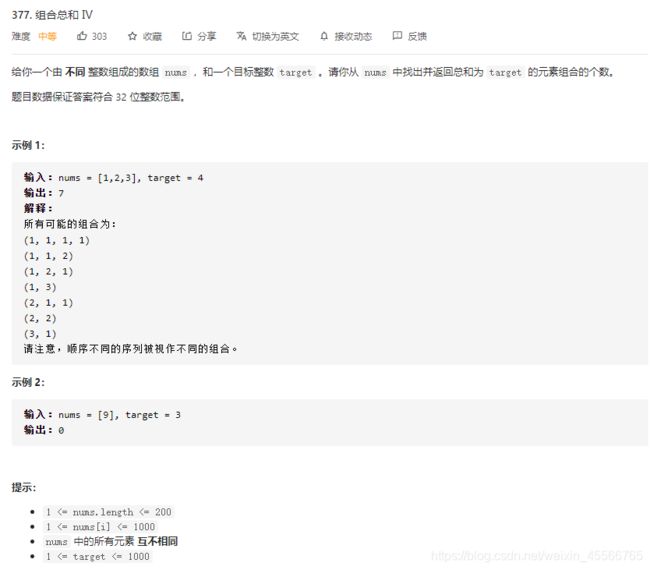
3.6 377. 组合总和 Ⅳ

用dfs做只能过7个样例，
[1,50]
200
会超时，还是得用背包问题去解决：

dfs代码

class Solution {
public:
    int res = 0;
    vector<int> path;
    int combinationSum4(vector<int>& nums, int target) {
        sort(nums.begin(),nums.end());
        dfs(0,nums,target);
        return res;
    }
    void dfs(int u,vector<int>& nums, int target)
    {

        if( target < 0)
            return;
        if(0 == target)
        {
            for(int i = 0; i < path.size(); i++)
                cout << path[i] << " ";
            cout << endl;
            res++;
            return;
        }

        for(int i = u;i < nums.size();i++)
        {
            target -= nums[i];
            path.push_back(nums[i]);
            dfs(u,nums,target);
            target += nums[i];
            path.pop_back();
        }
    }
};

dp代码

这一题类似于整数划分，但是这里的方案可以重复比如 [1,1,2]、[1,2,1]等。
利用整数划分的代码，下面代码对于题目中的样例结果为4，是不重复的方案数，实际结果是7

class Solution {
public:
    int f[210][1010] = {0};
    int combinationSum4(vector<int>& nums, int target) {
        int n = nums.size();
        for(int i = 0; i <= n;i++)
            f[i][0] = 1;
        for(int i = 1; i <=n;i++)
        {
            for(int j = 0; j <= target;j++)
            {
                f[i][j] = f[i-1][j];
                if( j >= nums[i-1])
                {
                    f[i][j] = f[i][j] + f[i][j-nums[i-1]];
                }
            }
        }
        return f[n][target];
    }
};