02神经网络的学习及代码实现

“学习”是指从训练数据中自动获取最优权重参数的过程。引入损失函数指标，学习的目的是以该损失函数为基准，找出尽可能小的损失函数的值。

1、从数据中学习

从数据中学习规律，模式，避免人为介入。

先从图像中提取特征量，再用机器学习技术学习这些特征量的模式。

常用的特征量包括SIFT、SURF和HOG等，使用特征量将图像数据转换为向量，然后对转换后的向量使用SVM、KNN等分类器进行学习。

这种方法也需要人工设计特征量。

深度学习是将图片输入，由算法提取特征量。

图1 人工设计规律到从数据学习

端对端（end-to-end）：从原始数据（输入）中获取目标结果（输出）的过程。

1.1 训练数据和测试数据

为了提高模型的泛化能力，必须将数据划分为训练集和测试集。

泛化能力：处理未被观察过的数据的能力。

获得泛化能力是机器学习的最终目标。当然对某个数据集过度拟合就会出现过拟合。

避免过拟合也是机器学习的重要课题。

2、损失函数（loss function)

神经网络的学习通过某个指标表示现在的状态，然后以这个指标为基准，寻找最优权重参数。神经网络学习中所用的这个指标为损失函数。一般用均方误差和交叉熵误差。

损失函数表示神经网络性能的“恶劣程度”的指标。即网络对数据再多大程度上不拟合。

2.1 均方误差（mean squared error)

                                                            (1-1)

其中：

y为神经网络的输出；t为监督数据，k为维数。

比如：10个元素

y=[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]

t=[0,0,1,0,0,0,0,0,0,0]

y输出为概率，即0的概率为0.1，1的概率为0.05，2的概率为0.6等

t的表示方法称为one-hot表示。即只有正确标签为1，其余标签都为0的表示方法。

实现方法：

def mean_squared_error(y,t):
    returen 0.5*np.sum((y-t)**2)

例1:

t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]
mean_squared_error(np.array(y),np.array(t))

t标签为2，y2的概率也是最高。均值误差97.5%。

例2：正确标签为2，预测为7

t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.1,0,0.05,0.1,0,0.6,0,0]
mean_squared_error(np.array(y),np.array(t))

计算结果59.75%。

例1的误差较小，即输出结果与监督数据更加吻合。

2.2 交叉熵误差(cross entropy error)

                                                           (1-2)

交叉熵误差的值是由正确解标签对应的输出结果决定。

代码实现：

def cross_entropy_error(y,t):
    delta=1e-7
    return -np.sum(t*np.log(y+delta))

添加一个delta微小值可以防止负无限大的发生。

重复上面的例子

t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.6,0,0.05,0.1,0,0.1,0,0]
cross_entropy_error(np.array(y),np.array(t))

输出为0.51.

t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.1,0,0.05,0.1,0,0.6,0,0]
cross_entropy_error(np.array(y),np.array(t))

输出为2.3.

2.3 mini-batch学习

前面的介绍中只考虑是针对单个数据的损失函数。如果需要对N个数据进行计算，就要对前面的公式（1-1）和（1-2）除以N，即求数据的“平均损失函数”。但是如果数据量达到成百上千万，计算平均值计算量太大。所以从数据中选出一批数据（mini-batch，小批量），然后对mini-batch学习。这种方法称为mini-batch学习。

mini-batch版交叉熵误差实现代码：

def cross_entropy_error(y,t):
    if y.dim==1:
        t=t.reshape(1,t.size)
        y=y.reshape(1,y.size)
        
    batch_size=y.shape[0]
    return -np.sum(t*np.log(y+1e-7))/batch_size

当监督数据为非ont-hot表示时，代码如下：

def cross_entropy_error(y,t):
    if y.ndim==1:
        t=t.reshape(1,t.size)
        y=y.reshape(1,y.size)
        
    batch_size=y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size),1]+1e-7))/batch_size

2.4 为什么要设定损失函数？

既然目标是提高精度，为什么不把精度作为指标？

1、因为要去求最小值，需要求函数的导数。不用精度作为指标，是因为精度导数很多为0，导致参数无法更新。

2、精度微调参数，精度变化很小，有变化也会变成不连续、离散的值，而损失函数可以发生连续性的变化。

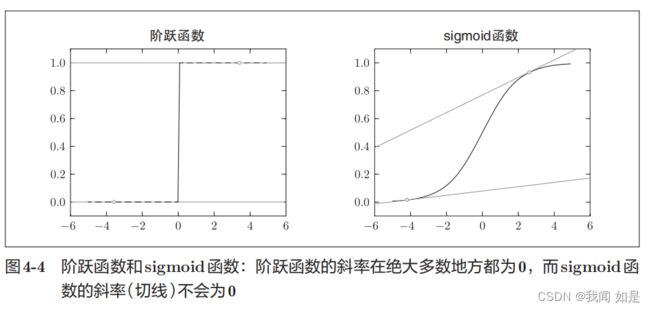
神经网络不使用阶跃函数作为激活函数，也是同样的道理。

3、数值微分

3.1 梯度法

机器学习的任务是再学习时寻找最优参数，神经网络也在学习时找到最优参数（权重和偏置）。即损失函数取最小值时的参数。

利用梯度来寻找函数最小值的方法就是梯度法。

梯度表示的是各点处的函数值减小最多的方向。复杂函数中，梯度指示的方向基本上都不是函数值最小处，但是沿着它的方向能够最大限度地减小函数的值。所以寻找函数最小值要以梯度信息为线索，决定前进的方向。

通过不断沿梯度方向前进，逐渐减小函数值的过程就是梯度法。

寻找最小值的梯度法称为梯度下降法（gradient descent method)，寻找最大值的梯度法称为梯度上升法（gradient ascent method)。深度学习中，梯度法主要是指梯度下降法。

                                      （1-3）

表示更新量，称为学习率。

梯度下降法实现代码：

#梯度
def numerical_gradient(f,x):
    h=1e-4
    grad=np.zeros_like(x)
    
    for idx in range(x.size):
        tmp_val=x[idx]
        x[idx]=tmp_val+h
        fxh1=f(x)
        
        x[idx]=tmp_val-h
        fxh2=f(x)
        
        grad[idx]=(fxh1-fxh2)/(2*h)
        x[idx]=tmp_val
        
    return grad

#梯度下降法
#lr：学习率
#init_x：初始值
#step_num:重复次数
def gradient_descent(f,init_,lr=0.01,step_num=100):
    x=init_x
    
    for i in range(step_num):
        grad=numerical_gradient(f,x)
        x-=lr*grad
        
    return x

设定合适的学习率很重要。学习率称为超参数。超参数由人工设定。

4、神经网络的学习步骤

4.1 设置 mini-batch

由于mini-batach是随机选取的，又称为随机梯度下降法(stochastic gradient descent,SGD)。

4.2 计算梯度

4.3 更新参数

4.4 重复4.1~4.3