论文阅读：Learning Lens Blur Fields

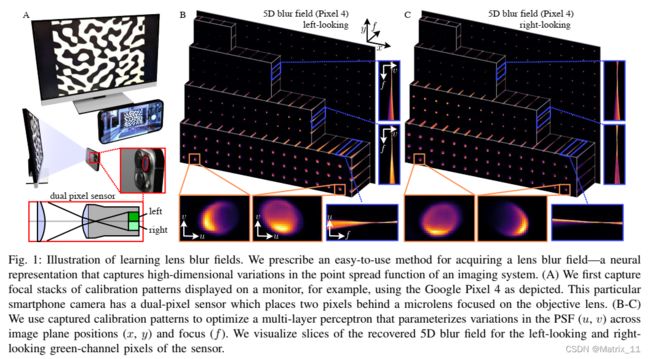
这篇文章是对镜头模糊场进行表征学习的研究，镜头的模糊场也就是镜头的 PSF 分布，镜头的 PSF 与物距，焦距，光学系统本身的像差都有关系，实际的 PSF 分布是非常复杂而且数量也很多，这篇文章提出用一个神经网络 MLP 来进行表征学习，相当于将镜头的 PSF 分布都压缩在了一个神经网络模型里面。

Abstract

光学模糊是光学镜头的固有性质，因为实际镜头都存在各种各样的像差，光学模糊与物距，焦距，入射光线的波长都有关系。光学镜头的表现可以用点扩散函数，也就是 PSF 来表示，实际镜头的 PSF 场非常复杂。这篇文章提出一种标定的方法，来构建这样一个实际光学镜头的 PSF 场，然后设计了一个高维的神经表征来学习这个 PSF 场。文章中用 MLP 来建模这个神经表征，这个镜头模糊场，可以准确地获得镜头在成像面的不同成像位置，不同对焦设置以及不同深度下的 PSF；这些不同的 PSF 都可以表示成与 sensor 有关的一个函数。这个神经网络的表征，同时考虑了镜头的离焦，衍射效应，以及各种像差，同时也考虑了特定 sensor 的性质，比如 color filters 以及与 pixel 有关的 micro lens。为了学习实际摄像模组的模糊场，文章将此形式化成一般的非盲反卷积问题，通过一批少量的实采数据构成的 focal stack，直接训练这个 MLP 网络结构。同时文章也构建了第一个与镜头模糊场相关的数据集，而且这个数据集是一个 5 维的模糊场的数据集。这套方法，可以很方便地快速迁移到不同的镜头模组上。

Introduction

一个实际的光学成像系统，需要考虑到镜头的离焦，像差，以及衍射效应等，如何精确地刻画这些性质对成像系统的影响，是一个非常大挑战，而且这个问题随着自动驾驶，以及手机摄影的兴起，也已经变得越来越重要了。

光学模糊一般是用 PSF 来刻画，PSF 也叫点扩散函数，表示的是一个理想点光源通过镜头到达 sensor 像面上的能量分布，真实光学系统的 PSF 建模是一个非常挑战的问题，因为 PSF 与很多因素包括光源，物距，焦距设置，波长等都有关系。

目前 PSF 的表示有三种方法，参数法，非参数法，以及基于几何或者傅里叶光学的模拟方法：

• 参数法，基于理想的镜头或者成像模型来表示 PSF，比如基于高斯分布，泽尼克系数，塞德尔系数等方式，这类方法的表示能力有限
• 非参数法，一般是通过对 sensor 像面进行一系列的采样来估计 PSF，这类方法需要通过反卷积的方法来求解出当前光学系统的 PSF，或者通过设置一个点光源，逐步扫描的方式，获取 sensor 像面上每个位置的 PSF，这类方法相对来说会更为准确，但是效率比较低
• 模拟法，是通过将光学系统进行物理成像模拟，仿真得到光学系统的 PSF，这类方法需要真实的光学系统参数，有的时候，实际的光学设备很难获取到这些参数

上面这些方法，估计出来的 PSF 都是独立存在的，有多少个 PSF，就需要存多少个 PSF，本文的一个创新点还在于把整个 PSF 的空间分布，用一个更加紧凑的神经网络来表示。文章中用的是 MLP，一个非常经典的神经网络，神经网络的拟合能力已经是众所周知的强大，可以拟合非常连续的 PSF 分布，以及非常复杂的 PSF 的形态，为了训练这样一个 MLP, 也需要构建相应的数据集，所以文章也提出了一种高效地构建 PSF 数据集的方法，所以总得来说，文章的主要创新有两点：

• 实际成像系统的 PSF 分布的标定与构建，文章提出了一种方法，可以对不同的成像设备，包括手机，单反都能进行 PSF 的标定与估计
• 利用神经网络 MLP 对镜头模糊场 PSF 的分布进行拟合，形成一个更加紧凑的镜头模糊场的表示

Learning lens blur fields

文章整个的 pipeline 如下所示：

Lens Blur Field Representation

假设真实环境中有一个点光源 $\mathbf{p}\in {\mathbb{R}}^3$ 距离镜头为 $d$，通过透视投影，点光源从三维空间投影到二维的相机平面，投影后的坐标为 $\tilde{\mathbf{x}}\in {\mathbb{R}}^2$，然后通过镜头的内参，最后转换到图像平面，其坐标为 $\mathbf{x}\in {\mathbb{R}}^2$，从三维空间投影到二维图像平面，与镜头的焦距 $f$，成像的物距 $d$ 以及sensor 的类型 $c$ 有关，dual-pixel 类型的 sensor 会有一个视差，最终的图像坐标与三维空间坐标的映射关系可以表示成如下所示：

$$\mathbf{x}=\text{invproj}(\mathbf{x},d,f,c)\text{\hspace{1em}(1)}$$

整个镜头的模糊场，表示为 ${\text{PSF}}_{\theta }(\mathbf{x},d,f,\mathbf{u})$，其中 $\theta$ 表示神经网络 MLP 的参数，${\text{PSF}}_{\theta }(\mathbf{x},d,f,\mathbf{u})$ 描述的是距离点光源 $\mathbf{p}$ 在像面的投影 $\mathbf{x}$ 为 $\mathbf{u}$ 的范围内的能量分布，或者说理想点光源模糊成什么样子。其中的 $c$ 表示与 sensor 类型相关，或者说与 PSF 的形态相关的参数，对于普通的 Bayer 模式的 sensor，$c$ 是 4，对于黑白 sensor 来说，$c$ 是 1，对于带 dual-pixel 类型的 sensor 来说，需要在原来的基础上乘以 2

Continuous Image Formation

假设镜头对距离其为 $d$ 的一个平面成像，如果是理想成像，那就是没有模糊的成像

$${\hat{I}}^{(c)}(\mathbf{x},d,f)=A^{(c)}(\mathbf{p})E^{(c)}(\mathbf{p},f)\text{\hspace{1em}(2)}$$

其中，$A^{(c)}(\mathbf{p})$ 表示真实平面的光照性质，体现了真实的环境光照与平面材质相互作用下的光照性质，$E^{(c)}(\mathbf{p},f)$ 表示能量效率，最终实际的模糊图像可以由如下的表达式表示：

$$I^{(c)}(\mathbf{x},d,f)={\int }_{\mu }{\text{PSF}}_{\theta }(\mathbf{x},d,f,\mathbf{u})\cdot {\hat{I}}^{(c)}(\mathbf{x}-\mathbf{u},d,f)d\mathbf{u}\text{\hspace{1em}(3)}$$

$\mathbf{u}$ 表示 $\mathbf{x}$ 的一个邻域范围。

为了能够学习这个模糊场的神经表示，可以构建如下的损失函数：

arg min ⁡ θ ∑ t , c , i ; x ∈ P ∥ I ( c ) ( x , d i , f i ) − ∑ u PSF θ ( c ) ( x , d i , f i , u ) ⋅ I ^ t ( c ) ( x − u , d i , f i ) ∥ 2 2 (4) \argmin_{\theta} \sum_{t,c,i; \mathbf{x}\in \mathcal{P}} \left \| {I}^{(c)}(\mathbf{x}, d_{i}, f_{i}) - \sum_{\mathbf{u}} \text{PSF}_{\theta}^{(c)}(\mathbf{x}, d_i, f_i, \mathbf{u}) \cdot \hat{I}_{t}^{(c)}(\mathbf{x} - \mathbf{u}, d_i, f_i) \right \|_{2}^{2} \tag{4} θargmin​t,c,i;x∈P∑​ ​I(c)(x,di​,fi​)−u∑​PSFθ(c)​(x,di​,fi​,u)⋅I^t(c)​(x−u,di​,fi​) ​22​(4)

$$\text{subject to}{\text{PSF}}_{\theta }^{(c)}\ge 0$$

表达式 (4) 里外面的求和表示对所有像素的通道 $c$，所有的 sensor 像素点 $\mathbf{x}$，所有的焦距 $f_i$ 及物距 $d_i$，其中 $ 1 \le i \le N_{I}$，以及对所有的sensor类型，$ 1 \le t \le N_{T}$，表达式内的求和，表示一个卷积的离散求和形式，是对公式（3）的一个近似，如果 $d$ 是一个固定的物距，那么所表示的模糊场是一个 5 维的模糊场 $(f,t,c,\mathbf{x},\mathbf{u})$，如果 $d$ 也是一个变量，那就是一个 6 维的模糊场 $(d,f,t,c,\mathbf{x},\mathbf{u})$。

文章中使用 MLP 来表示这样一个模糊场，为了训练这样一个 MLP，文章中是通过获取 RAW 图来进行训练，同时只对 RAW 图上能够测量的通道像素值进行卷积求和，也就是说 RAW 图会进行通道拆分，然后每个通道单独计算当前通道的 PSF，文章中用到的 MLP 有 7 层，最后一层用的是 sigmoid 激活函数，其它层的激活函数是 RELU。

为了提升计算效率，文章中也假设 PSF 在一个局部区域内可以认为是相对类似的，细微的变化几乎可以忽略不计，这样对 $\mathbf{x}$ 采样的时候，可以不用采得很密，可以每个 patch 估计一个 PSF，文章中将每个 patch 的大小定义为 PSF size 的 1.5 倍。

Image Acquisition Procedure

接下来，文章介绍了如何获取有模糊图像以及没有模糊的图像以构成训练数据对，整个流程步骤如上图所示，通过透视投影，畸变，以及 shading 获得一张没有模糊的图像 ${\hat{I}}^{(c)}$ ，同时通过拍摄屏幕获得一张模糊图像 $I^{(c)}$，模糊图像类似通过了镜头的光学像差的退化，没有模糊的图像类似通过镜头前的真实场景，因为从真实场景到镜头成像之间，还有坐标的变换，畸变以及 shading 的影响，所以为了让这两张图像对齐，需要做预处理。

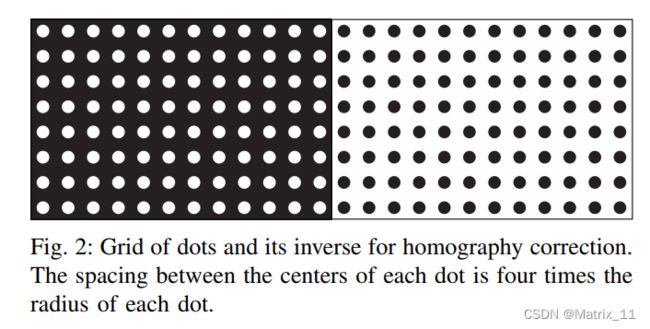
• Homography Estimation，首先是投影矩阵 $H$ 的估计，也就是单应性矩阵的估计，这一步是让没有模糊的图像与实际拍摄的图像进行坐标对齐，为了估计这样一个投影矩阵，需要进行标定，文章中使用了一组特定的 pattern，也就是两张图，一张是黑底上面有很多白色的圆点，另外一张是白底上面有很多黑色的圆点，如下图所示：

通过将 albedo dotgrid images 与拍摄的 dotgrid images 的圆点检测出来，然后计算这些圆点的圆心，圆心坐标在两张图像之间是不一样的，通过 RANSAC 算法计算这些匹配圆心之间的坐标转换关系，进而得到这个投影矩阵。

• Lens Distortion Estimation，第二个需要考虑的是镜头的放大率以及镜头的畸变，为了解决镜头的放大率的影响，文章中先拍摄一组 focal stack 的图像，然后合成一张全对焦的图像，然后估计每个 out-of-focus 图像中圆点圆心与全对焦图像圆点圆心的映射关系，这个映射关系是一个尺度关系，
  $S(\tilde{\mathbf{x}},d_i,f_i,c)$。至于镜头的畸变，文章中是用一个六阶的 Brown-Conrady 模型去模拟这个径向畸变 $D(\tilde{\mathbf{x}},c)$,这个畸变模型对所有的 $f_i,d_i$ 都一样。

• Radiometric Compensation，第三个要考虑的是 shading correction，文章中叫照度补偿，因为真实镜头的光照能量会呈现中间强，四周弱的分布，文章中用一张全黑图以及一张全白图来表示环境的最弱光照以及最强光照，拍摄这两张图之后，作为 $I_{min},I_{max}$，然后所有图像可以认为是这两张图像的一个线性组合：

$$\hat{I}(\mathbf{x})=[1-A(\text{invproj}(\mathbf{x},d_i,f_i))]I_{min}(\mathbf{x})+A(\text{invproj}(\mathbf{x},d_i,f_i))I_{max}(\mathbf{x})$$

• Image caputure, 前面介绍的是对 albedo 图像的预处理，albedo 图像类似理想图像，表示真实环境的光照分布，接下来是考虑实际成像，也就是实拍的图像，文章中是通过拍摄屏幕的方式来获取实际退化的图像，文章中用的是一个 32 英寸的 4K 显示屏，将镜头平行放置在屏幕前面某个距离下，然后进行拍摄，不同的距离，屏幕在镜头中的成像大小不同，近距离情况下，屏幕可以占满整个成像面，远距离情况下，屏幕只能占据像面的一部分，所以远距离情况下，需要移动镜头或者移动屏幕，以保证最终的屏幕能在整个成像面都有成像。

Results

最后是实验部分，文章对比了不同的方法，也对不同的镜头模糊场做了测试，包括仿真的 PSF，实际手机的镜头模糊场，以及实际单反的镜头模糊场。