算法练习-三数之和（思路+流程图+代码）

难度参考

        难度：中等

        分类：数组

        难度与分类由我所参与的培训课程提供，但需要注意的是，难度与分类仅供参考。且所在课程未提供测试平台，故实现代码主要为自行测试的那种，以下内容均为个人笔记，旨在督促自己认真学习。

题目

        给你一个整数数组nums,判断是否存在三元组[nums[i],nums[j],nums[k]]满足i!=j、i!=k且j!=k,同时还满足nums[i]+nums[j]+nums[k]=0。请你返回所有和为0且不重复的三元组。

        示例1:
        输入：nums=[-1,0,1,2,-1,-4]
        输出：[-1，-1,2]，[-1,0,1]

        解释：
        nums[0]+nums[1]+nums[2]=(-1)+0+1=0.
        nums[1]+nums[2]+nums[4]=0+1+(-1)=0.
        nums[0]+nums[3]+nums[4]=(-1)+2+(-1)=0.
        不同的三元组是[-1,0,1]和[-1，-1,2]。
        注意，输出的顺序和三元组的顺序并不重要。

        额外要求：
        ·答案中不可以包含重复的三元组

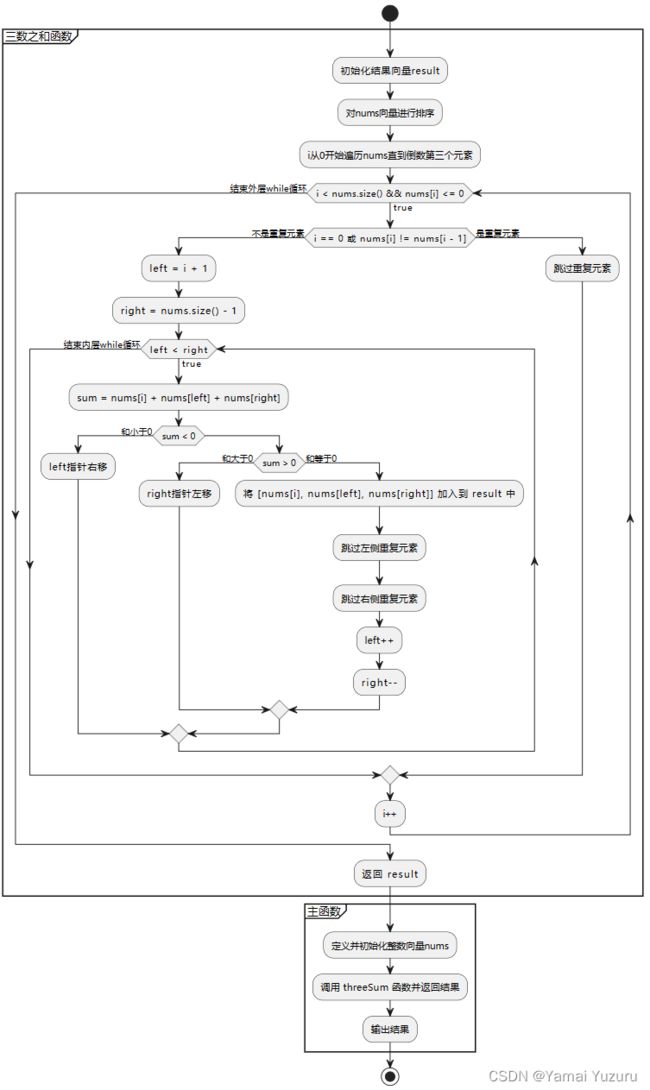
思路

        可以使用排序加双指针的方法来解决这个问题，先对数组排序，然后遍历数组，对于每个元素，使用双指针指向该元素之后的开始位置和结束位置，然后根据三个数字之和与0的比较结果来移动指针。具体步骤如下：

1. 对数组进行排序。
2. 遍历排序后的数组，对于索引 i 的元素，设置左指针 left 在 i+1 的位置，设置右指针 right 在数组末尾的位置。
3. 如果 nums[i] 大于 0，由于数组已经排序，nums[i] 之后的元素都会大于0，它们的和不可能为0，结束循环。
4. 如果当前索引 i 与前一个索引相同，则跳过当前循环，防止出现重复的三元组。
5. 当左指针小于右指针时，计算 nums[i]、nums[left] 和 nums[right] 的和。
6. 如果和为 0，添加到结果中，并且移动左右指针跳过相同的元素，防止重复。
7. 如果和小于 0，说明需要增加数值，左指针右移。
8. 如果和大于 0，说明需要减小数值，右指针左移。
9. 遍历完成后，返回结果。

示例

        假设我们有一组数字：[-1, 0, 1, 2, -1, -4]，我们希望找到所有唯一的三个数字组合，使得这三个数字的和为 0。

        我们按升序排序，得到：[-4, -1, -1, 0, 1, 2]。这是为了方便找到结果并避免重复。这样一来，在未来的时候，假设前一个left指向头一个出现的 -1，那么现在left 指向的 -1 与前一个 -1 是相同的。如果我们用这个 -1 作为三元组的一部分，它就会产生与前一个 left 指针位置相同的三元组。为了避免记录重复的三元组，我们只用检查临近的元素，判断之后继续移动 left，跳过所有相同的元素即可避免元素的重复。

1. 第一轮遍历：

   • 遍历的第一个数字是 -4，这是当前“基准数”。
   • left 指针在 -1（基准数的右边第一个位置）。
   • right 指针在 2（数组的最右端）。

             [-4, -1, -1, 0, 1, 2]
     基准数 :  ^
     left   :      ^
     right  :                   ^

           我们的目标是找到使得 -4 + (A[left]) + (A[right]) = 0 的A[left]和A[right]数值。当前 -4 + (-1) + (2) = -3，和小于0，我们需要一个更大的数，所以将 left 右移。

   • left 移动到第二个 -1，-4 + (-1) + (2) = -3，仍然小于0，我们再次移动 left。

             [-4, -1, -1, 0, 1, 2]
     基准数 :  ^
     left   :          ^
     right  :                   ^

   • left 指向 0 时，和为 -2，我们继续右移 left。

             [-4, -1, -1, 0, 1, 2]
     基准数 :  ^
     left   :             ^
     right  :                   ^

   • left 指向 1 时，和为 -1，继续。

             [-4, -1, -1, 0, 1, 2]
     基准数 :  ^
     left   :                ^
     right  :                   ^

   • 现在 left 和 right 相遇了，这一轮结束。由于 -4 的值太小，我们无法在不使用它的情况下得到和为0的三个数。

             [-4, -1, -1, 0, 1, 2]
     基准数 :  ^
     left   :                   ^
     right  :                   ^

2. 第二轮遍历：

   • 基准数 移动到第一个 -1。
   • left 指向第二个 -1。
   • right 仍然指向 2。

             [-4, -1, -1, 0, 1, 2]
     基准数 :      ^
     left   :          ^
     right  :                   ^

           我们同样寻找和为0的组合。现在有 -1 + (-1) + (2) = 0，我们找到了第一个有效的三数组合。

   • 记录这个组合，在上面的数组中为[-1, -1, 2]。

             [-4, -1, -1, 0, 1, 2]        记录： [-1, -1, 2]
     基准数 :      ^
     left   :          ^
     right  :                   ^

   • left 移动到下一位，为了避免重复需要跳过相同的值。但是因为后面立即就是 0，所以我们检查这个组合：

             [-4, -1, -1, 0, 1, 2]        记录： [-1, -1, 2]
     基准数 :      ^
     left   :             ^
     right  :                   ^

   • -1 + (0) + (2) = 1，总和大于0，不符合条件，我们需要减少数值。所以移动 right 指针向左。

             [-4, -1, -1, 0, 1, 2]        记录： [-1, -1, 2]
     基准数 :      ^
     left   :             ^
     right  :                ^

   • right 移动到 1，现在 -1 + (0) + (1) = 0，我们找到第二组和为0的三数组合。

   • 记录这个组合，在我们的数组中为[-1, 0, 1]。

             [-4, -1, -1, 0, 1, 2]        记录： [-1, -1, 2]
     基准数 :      ^                             [-1, 0, 1]
     left   :             ^
     right  :                ^

3. 接下来的遍历：
           由于我们开始的基准数是数组中第二个数，其实是第一个-1的重复值，我们也可以简单跳过它，避免重复工作。但是，如果我们继续操作，基准数将会移动到第二个 -1，然后重复上面步骤2的过程，并最终移动到 0，继续寻找组合，但是从0开始，我们不可能找到两个更小的数使它们的和为0，因为所有剩下的数都不够小。

                因此遍历结束，我们有了两组符合要求的组合:

• [-1, -1, 2]
• [-1, 0, 1]

        这些就是通过具体移动left和right指针，我们在例子数组中找到的所有唯一的三数之和等于0的组合。

梳理

        在三数之和的问题中，我们通常首先对数组进行排序，然后用一个循环遍历每个元素，将每个元素作为潜在的“基准数”来寻找其他两个数，使得它们的和为零。因为数组是排序过的，所以当我们在进行双指针查找其他两个数时，我们可以很容易地跳过重复的数字，以避免发现重复的三元组。

        当我们遇到一个和前一个数字相同的“基准数”时，意味着使用这个作为基准数的所有潜在的组合在前一个基准数中已经被检查过。因此，以这个重复的数字作为基准数去寻找新的配对没有意义，因为它只会给出与前一轮基准数相同的结果。为了避免重复工作，我们直接跳过重复的基准数。

        在这个例子中，我们有两个 -1 作为潜在的基准数。当我们使用第一个 -1 作为基准数时，我们已经找到了所有可能的有效组合，那么第二个 -1 就没有必要再次作为基准数进行同样的工作。

        关于基准数为 0的情况，我们知道两个数之和为零的情况只存在于它们互为正负的情况下。如果基准数为 0，要找到两个其他的数使得三数之和为零，那么这两个数必须是相等且符号相反的。但如果我们的基准数是第一个非负数（在排序的数组中为 0 或 正数），再往后（即右侧的元素）不可能找到两个和为负数的元素与其组合成和为零。因此，当遍历到 0 或更大的数作为基准数时，我们可以停止搜索。

代码

#include 
#include 
#include 

using namespace std;

vector> threeSum(vector& nums) {
    vector> result;
    sort(nums.begin(), nums.end());
    
    for (int i = 0; i < nums.size() && nums[i] <= 0; ++i) {
        if (i > 0 && nums[i] == nums[i-1]) continue; // 跳过重复元素
        
        int left = i + 1, right = nums.size() - 1;
        while (left < right) {
            int sum = nums[i] + nums[left] + nums[right];
            if (sum < 0) {
                ++left; // 需要增加数值，左指针右移
            } else if (sum > 0) {
                --right; // 需要减小数值，右指针左移
            } else {
                result.push_back({nums[i], nums[left], nums[right]});
                // 跳过所有相同的元素
                while (left < right && nums[left] == nums[left+1]) ++left;
                while (left < right && nums[right] == nums[right-1]) --right;
                ++left;
                --right;
            }
        }
    }
    return result;
}

int main() {
    vector nums = {-1, 0, 1, 2, -1, -4};
    vector> triples = threeSum(nums);
    
    for (const auto& triple : triples) {
        cout << "[" << triple[0] << "," << triple[1] << "," << triple[2] << "]" << endl;
    }

    return 0;
}

        时间复杂度：O(n^2)
        空间复杂度：O(1)

        push_back 正在向 result 向量的末尾添加一个新元素，这个新元素是由 nums[i]、nums[left]、nums[right] 构成的一个 vector。

打卡