基础算法——二分查找

一、二分查找的前置条件

         必须是有序的数组A才能使用二分查找！！！

二、二分查找的文字描述

        1、定义左边界L，右边界R，确定搜索的范围，循环执行二分查找（2、3步）

        2、获取中间值M = Floor((L+R)/2)  //向下取整 

        3、中间索引的值A[M]与与搜索值T进行比较

              ①  A[M] == T 表示找到，返回中间索引

              ②  A[M] > T 中间值右侧的值都大于T，无需比较，中间索引左边去找，M - 1设置为右边界，重新查找

              ③  A[M] < T 中间值左侧的值都大于T，无需比较，中间索引右边去找，M - 1设置为左边界，重新查找

        4、当L>R时，表示没有找到，应结束循环

三、二分查找的图形描述

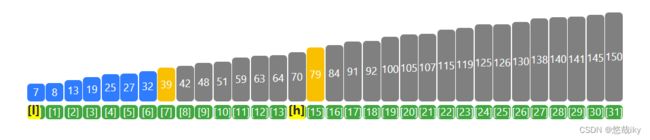
已有排序数组，查找32：

        1、第一次查找，79为中间值，32<79，在79左边查找

       2、第二次查找，39为中间值，32<39，在39左边查找

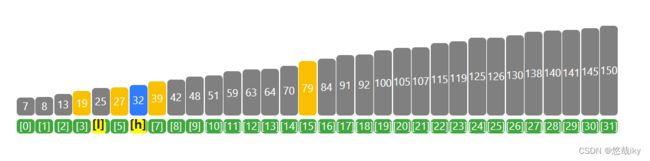
      3、第三次查找，19为中间值，32>19，在19右边查找

     4、第四次查找，27为中间值，32>27，在27右边查找

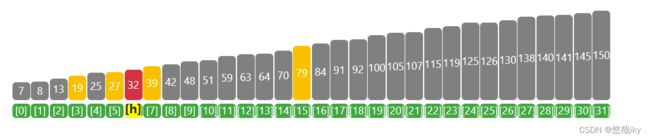
     5、第五次查找，32为中间值，32=32，返回索引值

四、二分查找代码

public class BinarySearch {
    public static void main(String[] args) {
        int[] array = {1, 5, 8, 11, 19, 22, 31, 35, 40, 45, 48, 49, 50};
        int target = 48;
        int idx = binarySearch(array, target);
        System.out.println(idx);
    }

    public static int binarySearch(int[] a, int t) {
        int l = 0, r = a.length - 1, m;
        while (l <= r) {
            m = (l + r) / 2;
            if (a[m] == t) {
                return m;
            } else if (a[m] > t) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return -1;
    }
}

五、细节问题

        在计算中间索引的时候L+R有可能整数溢出，我们应该修改代码避免这种现象。两个正整数相加，因为进位导致的符号位变化，导致两正数相加结果是负数。

        我这里给出两种解决思路：

        （1）(l+r)/2 ==> l/2 + r/2  ==>  l - (-l/2 + r/2)  ==>  l + (r-l)/2

                说明：这样替换即可避免整数溢出问题

        （2）(l+r)/2 ==> (l+r) >>> 2

                说明：将其替换成无符号的移位运算，右移一位，这样子不光能解决整数溢出问题，而            且效率比第一种高，因为右移运算的时钟周期比除法运算小，注意不能和除以2完全相等，            因为如果l+r是负数，将不等效/2

         实际上，二分还有很多变体，一旦使用变体，实现代码的左右边界选取会用变化，后续有时间将会补充。