AwyaW1217

数据结构——二叉树

树形结构：有向无环图树是图的一种

树形结构有一个根节点

没有回路

根节点：A

叶子节点：下面没有其他节点

节点：既不是根节点，也不是叶子节点的普通节点

树的度：树中有最多叉的节点有多少个插叉，这棵树的度就为多少

树的深度：树最深有几层深度就为几

二叉树：

树的度最多为2的树形结构

满二叉树：

所有叶子节点都在最底层

每个风叶子节点都有两个子节点

完全二叉树：

国内定义：

叶子节点都在最后一层或倒数第二层

叶子节点都向左聚拢

国际定义:

叶子节点都在最后一层或倒数第二层

如果有叶子节点，则必然有两个叶子节点

在二叉树中，每个节点都认为自己是根节点

子树：二叉树中，每一个节点或叶子节点，都是一棵子树的根节点

左子树、右子树：

传递二叉树要传根节点

树的遍历

前序遍历：先根次序遍历前->左->右前：当前

中序遍历：先根次序遍历左->前->右

后序遍历：先根次序遍历左->右->前

先构建一个树

function Node (value) {
    this.value = value
    this.left = null
    this.right = null
}
var a = new Node('a')
var b = new Node('b')
var c = new Node('c')
var d = new Node('d')
var e = new Node('e')
var f = new Node('f')
var g = new Node('g')
a.left = c
a.right = b
b.left = d
b.right = e
c.left = f
c.right = g

1.前序遍历

function getTree (node) {
    if (node == null) return
    console.log(node.value)
    getTree(node.left)
    getTree(node.right)
}
getTree(a)

2.中序遍历

function getTree (node) {
    if (node == null) return
    getTree(node.left)
    console.log(node.value)
    getTree(node.right)
}
getTree(a)

3.后序遍历

function getTree (node) {
    if (node == null) return
    getTree(node.left)
    getTree(node.right)
    console.log(node.value)
}
getTree(a)

二叉树的还原

准备一下，前序、中序、后续遍历数组，以及创建树节点函数

function changeToLowerCase (item) {
    return Array.from(item).map(o => o.toLowerCase())
}
//懒得写小写数组了，转换了一下，可直接代入原始小写数组哦
var arr1 = changeToLowerCase('ACFGBDE')//arr1 (7) ['a', 'c', 'f', 'g', 'b', 'd', 'e']
var arr2 = changeToLowerCase('FCGADBE')//arr2 (7) ['f', 'c', 'g', 'a', 'd', 'b', 'e']
var arr3 = changeToLowerCase('FGCDEBA')//arr3 (7) ['f', 'g', 'c', 'd', 'e', 'b', 'a']
function Node (value) {
    this.value = value
    this.left = null
    this.right = null
}

前序和中序还原一棵二叉树

function restore (arr1, arr2) {
    if (arr1 == null || arr2 == null || arr1.length == 0 || arr2.length == 0 || arr1.length !== arr2.length) return null
    var root = new Node(arr1[0])//先确定根节点
    var index = arr2.indexOf(root.value)//找到根节点在中序遍历数组中的位置索引
    var arr1Left = arr1.slice(1, 1 + index)//前序遍历左子树
    var arr1Right = arr1.slice(1 + index, arr1.length)//前序遍历右子树
    var arr2Left = arr2.slice(0, index)//中序遍历左子树
    var arr2Right = arr2.slice(index + 1, arr2.length)//中序遍历右子树
    root.left = restore(arr1Left, arr2Left)//根据左子树的前序和中序 还原左子树 并赋值给root.left
    root.right = restore(arr1Right, arr2Right)//根据右子树的前序和中序 还原右子树 并赋值给root.right
    return root
}
console.log(restore(arr1, arr2))

中序和后序还原一棵二叉树

function restore (arr2, arr3) {
    if (arr3 == null || arr2 == null || arr3.length == 0 || arr2.length == 0 || arr3.length !== arr2.length) return null
    var root = new Node(arr3[arr3.length - 1])//先确定根节点
    var index = arr2.indexOf(root.value)//找到根节点在后序遍历数组中的位置索引
    var arr2Left = arr2.slice(0, index)//中序遍历左子树
    var arr2Right = arr2.slice(index + 1, arr2.length)//中序遍历右子树
    var arr3Left = arr3.slice(0, index)//后序遍历左子树
    var arr3Right = arr3.slice(index, arr3.length - 1)//后序遍历右子树
    root.left = restore(arr2Left, arr3Left)//根据左子树的后序和中序 还原左子树 并赋值给root.left
    root.right = restore(arr2Right, arr3Right)//根据右子树的后序和中序 还原右子树 并赋值给root.right
    return root
}
console.log(restore(arr2, arr3))

二叉树的搜索

树的搜索、图的搜索、爬虫的逻辑、搜索引擎的爬虫算法

深度优先搜索：更适合探索未知
广度优先搜索：更适合探索局域

1.深度优先搜索

//对于二叉树来说，深度优先搜索 和 前序遍历顺序是一样的 
function deepSearch (root, target) {
    if (root == null) return false
    if (root.value == target) return true
    var left = deepSearch(root.left, target)
    var right = deepSearch(root.right, target)
    return left || right
}
console.log(deepSearch(a, 'd'))//true

2.广度优先搜索

function breadthSearch (rootList, target) {
    if (rootList == null || rootList.length == 0) return false
    var childList = []//当前层所有节点的子节点，都在这个list中，这样传入下一层级时候，就可以遍历整个层级的集合
    for (let i = 0; i < rootList.length; i++) {
        console.log(rootList[i])
        if (rootList[i] != null && rootList[i].value == target) {
            return true
        } else {
            childList.push(rootList[i].left)
            childList.push(rootList[i].right)
        }
    }
    return breadthSearch(childList, target)
}
console.log(breadthSearch([a], 'c'))//true

有点问题，需要改进。如果传入target为“n”，则报错

后续待优化

二叉树的比较

1.首先准备第二棵树

var a1 = new Node('a')
var b1 = new Node('b')
var c1 = new Node('c')
var d1 = new Node('d')
var e1 = new Node('e')
var f1 = new Node('f')
var g1 = new Node('g')
a1.left = c1
a1.right = b1
b1.left = d1
b1.right = e1
c1.left = f1
c1.right = g1

2. 左右不能互换，左子树与左子树比较、右边和右边比较

function compare (root1, root2) {
    if (root1 == root2) return true//是同一棵树
    if (root1 == null || root2 == null) return false
    if (root1.value != root2.value) return false//相同位置值不相等
    var leftBool = compare(root1.left, root2.left)//判断左子树是否相等
    var rightBool = compare(root1.right, root2.right)//判断右子树是否相等
    return leftBool && rightBool
}
console.log(compare(a, a1))//true

遇到二叉树比较问题时，必须要确定，左右两棵子树如果交换位置，即左右互换，算不算同一棵二叉树

默认互换后不是同一棵

面试时问确定规则

3.左右交换算同一棵

function compare (root1, root2) {
    if (root1 == root2) return true//是同一棵树
    if (root1 == null || root2 == null) return false
    if (root1.value != root2.value) return false//相同位置值不相等
    var leftBool = compare(root1.left, root2.left)//判断左子树是否相等
    var rightBool = compare(root1.right, root2.right)//判断右子树是否相等
    //左右可互换情况
    var leftBool1 = compare(root1.left, root2.right)//判断左子树与右子树是否相等
    var rightBool1 = compare(root1.right, root2.left)//判断右子树与左子树是否相等
    return leftBool && rightBool || leftBool1 && rightBool1
}
console.log(compare(a, a1))//true

二叉树diff算法

如图所示，比较以下两棵树

1.首先构建要比较的树

var a1 = new Node('a')
var c1 = new Node('c')
var e1 = new Node('e')
var f1 = new Node('f')
var g1 = new Node('g')
var x1 = new Node('x')
var z1 = new Node('z')
a1.left = c1
a1.right = x1
x1.right = e1
c1.left = f1
c1.right = g1
g1.right = z1

2.diffTree算法

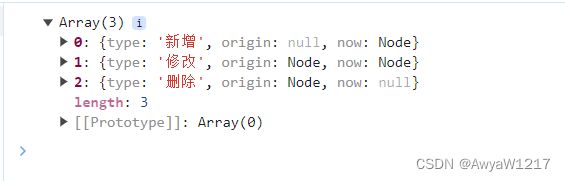
// 新增了什么 修改了什么 删除了什么
var diffList = []
function difftree (root1, root2, diffList) {
    if (root1 == root2) return diffList
    if (root1 == null && root2 != null) {//新增了节点
        diffList.push({ type: '新增', origin: null, now: root2 })
    } else if (root1 != null && root2 == null) {//删除了节点
        diffList.push({ type: '删除', origin: root1, now: null })
    } else if (root1.value != root2.value) {//相同的位置节点值不同，修改了节点
        diffList.push({ type: '修改', origin: root1, now: root2 })//修改后也要走diffTree 因为修改当前节点 不代表所有子节点都变了
        difftree(root1.left, root2.left, diffList)
        difftree(root1.right, root2.right, diffList)
    } else {
        difftree(root1.left, root2.left, diffList)
        difftree(root1.right, root2.right, diffList)
    }
    return diffList
}
console.log(difftree(a, a1, diffList))

3.最后结果呈现

白的也一样，那个方便看那个~

二叉搜索树（二叉排序树）

首先这是一棵搜索树

其次有排序的效果，左子树的节点都比当前节点小，右子树的节点都比当前节点大

//制作一个随机数组
var arr = []
for (let i = 0; i < 10000; i++) {
    arr[i] = Math.floor(Math.random() * 10000)
}
var num = 0
function search (arr, target) {
    for (let i = 0; i < arr.length; i++) {
        num += 1
        if (arr[i] == target) return true
    }
    return false
}
function Node (value) {
    this.value = value
    this.right = null
    this.left = null
}
function addNode (root, num) {
    if (root == null) return
    if (root.value == num) return
    if (root.value < num) {//目标值比当前节点大
        if (root.right == null) root.right = new Node(num)//右侧为空 则创建新节点 将目标值放在该位置
        else {
            addNode(root.right, num)//右侧不为空 则向右侧进行递归
        }
    } else {//目标值比当前节点小
        if (root.left == null) {
            root.left = new Node(num)
        }
        else {
            addNode(root.left, num)
        }
    }
}
function buildSearchTree (arr) {
    if (arr == null || arr.length === 0) return null
    var root = new Node(arr[0])
    for (let i = 1; i < arr.length; i++) {
        addNode(root, arr[i])
    }
    return root
}
var num2 = 0
function searchByTree (root, target) {
    if (root == null) return false
    num2 += 1
    if (root.value == target) return true
    if (root.value > target) {
        return searchByTree(root.left, target)
    } else {
        return searchByTree(root.right, target)
    }
}
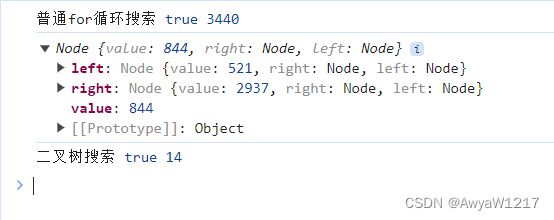
console.log("普通for循环搜索", search(arr, 2344), num)
var root1 = buildSearchTree(arr)
console.log(root1)
console.log("二叉树搜索", searchByTree(root1, 2344), num2)

平衡二叉树

根节点的左子树与右子树的高度差不能超过1
这棵树每个子树都符合第一条

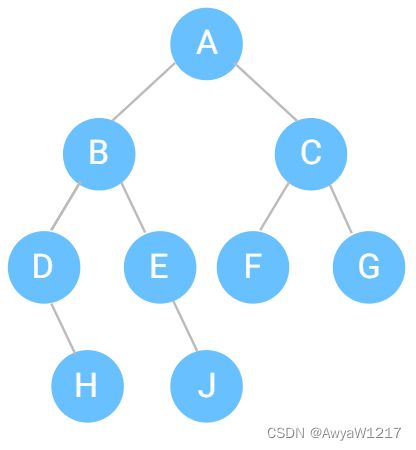
1.二叉树准备工作

function Node (value) {
    this.value = value
    this.left = null
    this.right = null
}
var a = new Node('a')
var b = new Node('b')
var c = new Node('c')
var d = new Node('d')
var e = new Node('e')
var f = new Node('f')
var g = new Node('g')
var h = new Node('F')
var j = new Node('J')
a.left = b
a.right = c
b.left = d
b.right = e
c.left = f
c.right = g
d.right = h
e.right = j

2.计算左右子树层深判断是否为平衡二叉树

function getDeep (root) {
    if (root == null) return 0
    var leftDeep = getDeep(root.left)
    var rightDeep = getDeep(root.right)
    return Math.max(leftDeep, rightDeep) + 1//算出左右子树层深后再加当前一层
}
function isBalance (root) {
    if (root == null) return true
    var leftDeep = getDeep(root.left)
    var rightDeep = getDeep(root.right)
    if (Math.abs(leftDeep - rightDeep) > 1)//绝对值大于1 则不平衡
    {
        return false
    } else {
        return isBalance(root.left) && isBalance(root.right)
    }
}
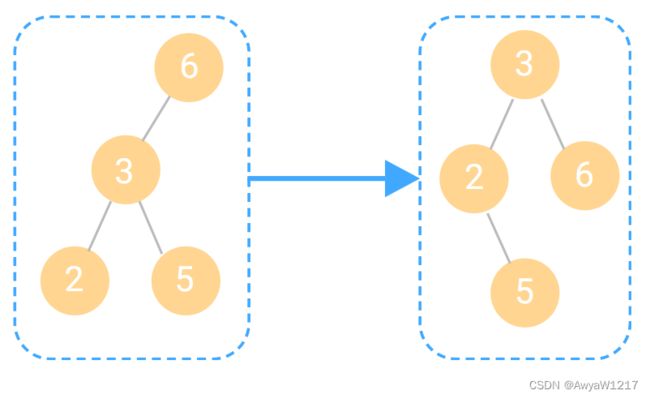
console.log(isBalance(a))//false

二叉树的单旋操作（左单旋，右单旋）

某一节点不平衡

1.左单旋

如果左边浅，右边深，进行左单旋

左单旋时

旋转节点：当前不平衡的节点

新根：右子树的根节点

变化分支：旋转节点的右子树的左子树

不变分支：旋转节点的右子树的右子树

旋转节点：不平衡的节点为旋转节点（2）

新根：旋转之后称为根节点的节点（5）

变化分支：父级节点发生变化的分支（3）

不变分支：父级节点不发生变化的分支（6）

to do list

找到新根
找到变化分支
当前旋转节点的右孩子为变化分支
新根的左孩子为旋转节点
返回新的根节点

2.右单旋

右单旋时

旋转节点：当前不平衡的节点

新根：左子树的根节点

变化分支：旋转节点的左子树的右子树

不变分支：旋转节点的左子树的左子树