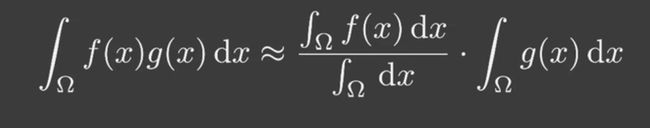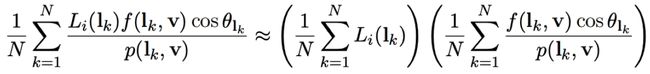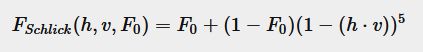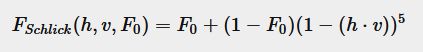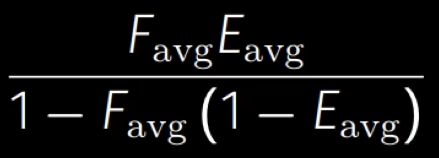高质量实时渲染笔记
文章目录
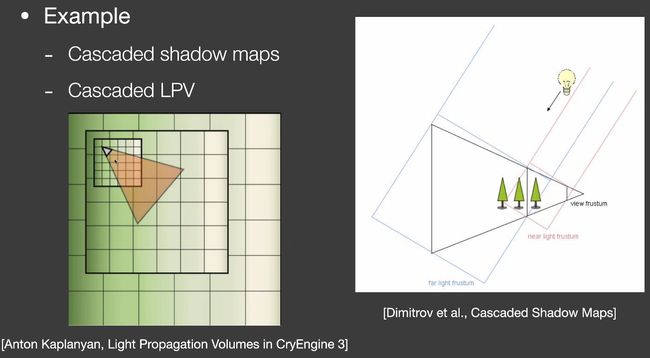
- Real-time shadows
-
- 1 自遮挡问题
- 2 解决阴影detach问题?
- 3 Aliasing
- 4 近似积分
- 5 percentage closer soft shadows(PCSS)
-
- percenta closer filtering(PCF)
- PCSS的思想
- 6 Variance Soft Shadow Mapping (VSSM)
-
- 步骤
- Moment Shadow Mapping
- 7 Distance field shadow
- Real-time Environment Mapping
-
- 1 The Split Sum
-
- 1. 计算入射光的积分:prefilter the environment
- 2. 计算brdf的积分:
- 2 Spherical Harmonics
-
- Spherical harmonics的性质
- 3 得到环境光照下的阴影
-
- 3.1 解决方案1
- 3.2 在环境光照下的渲染
- PRT
-
- Diffuse Case
- Glossy Case
- 缺点
- Real-time Global Illumination
-
- Reflective Shadow Maps(RSM)
-
- 注意事项
- 缺点
- Light Propagation Volumes(LPV)
-
- 步骤
- Voxel Global Illumination(VXGI)
-
- pass from light(决定哪些patch会被照亮)
- pass from camera
- 注意事项
- Screen Space Ambient Occlusion(SSAO)
-
- 特点
- 主要思想
- AO部分
- SS部分
- Screen Space Directional Occlusion SSDO
-
- SSAO和SSDO的比较
- Screen Space Reflection(SSR)
-
- 改进
- Physically-based Material(surface models)
-
- Cook-Torrance reflectance equation
- Normal distribution function(NDF)
- Geometry function
- Fresnel equation
-
- 解决能量不守恒问题
- Linearly Transformed Cosines线性变换余弦(LTC)
- Disney Principal BRDF
-
- PBR材质的缺点
- Non-Photorealistic Rendering(NPR)
-
- Outline Rendering
-
- shading 方法做描边
- 用图像的方法描边
- Color blocks
- Strokes Surface Stylization
- Real-time Raytracing
-
- 目标1. Quality(如果滤波太重了会有overblur,no artifac,keep all details)
- 工业界的解决方案
- The G-Buffers
- Back Projection
- 降噪过程
- Temporal失败的场景
- 解决方法
- 滤波的实现
-
- 高斯滤波
- Bilateral filtering 双边滤波
- Joint Bilateral Filtering
- filter的加速方法
-
- Separate Passes
- Progressively Growing Sizes
-
- 为什么可以这么做?
- Outlier Removal
-
- Temporal Clamping
- SVGF - Spatiotemporal Variance-Guided Filtering
-
- Depth
- Normal
- Luminance
- RAE - Recurrent denoising AutoEncoder
-
- Key architecture design
- 比较
- 工业界的一些解决方案
-
- Temporal Anti-Aliasing(TAA)
- SSAA(supersampling) vs MSAA(Multisample)
- Image based anti-aliasing solution
- Temporal Super Resolution
- Deferred Shading
-
- 步骤
- 问题
- Tiled Shading
- Cluster Shading
- Level of Detail Solutions
-
- key challenge
- Lumen
-
- Software ray tracing
- Hardware ray tracing
- 剩余的内容
Real-time shadows
1 自遮挡问题
加bias
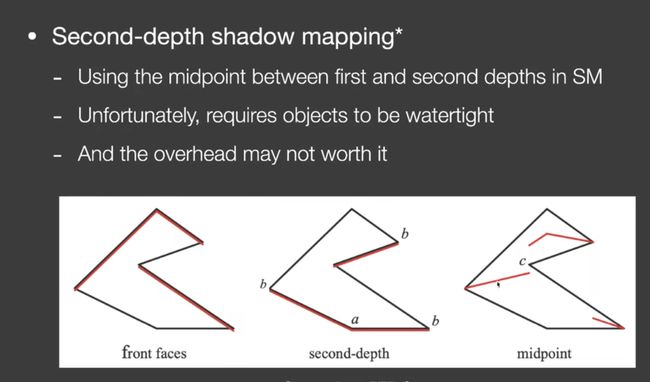
2 解决阴影detach问题?
问题:要求water tight(地板就不行)
3 Aliasing
cascade
4 近似积分
- g的support很小,积分域较小(small support point/directional lighting)
- g足够光滑 smooth integrand(diffuse bsdf/constant radiance area lighting)

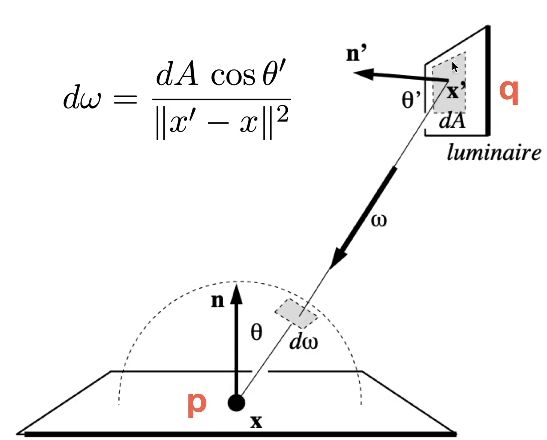
渲染方程,把visibility拆出来,拆成visibility部分和shading部分。
5 percentage closer soft shadows(PCSS)
shadow mapping是硬阴影。
percenta closer filtering(PCF)
PCF主要用来做抗锯齿的,但是可以用来做软阴影。
在阴影判断的时候做filtering。
对每一个着色点,采样周围一圈深度(比如3x3),和实际采样点深度比较,对这些深度取平均。
PCSS的思想
阴影的接受物和阴影的投射物,即遮挡的距离越近,阴影越近。
relative average projected blocker depth
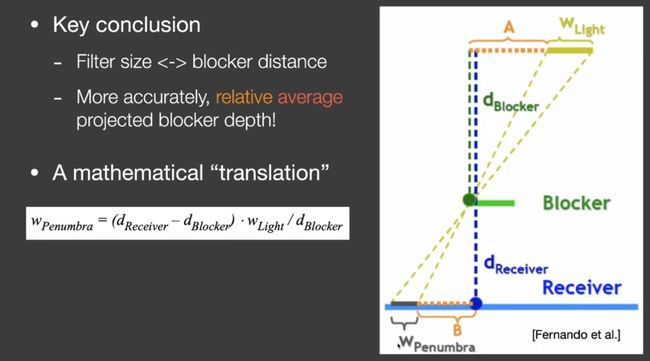
- 计算blocker深度(找到一定范围区域的平均blocker深度),具体做法是着色点和点光源连线(面光源近似成点光源)
- penumbra esimation
- percentage closer filter
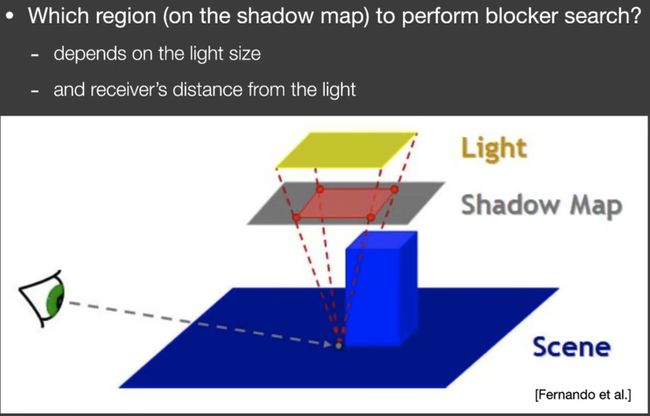
如何判断blocker的采样大小?(其实是平均的blocker size)
6 Variance Soft Shadow Mapping (VSSM)
解决PCSS中blocker search和filter慢的问题。
问题是采样太多,利用分布函数解决采样问题。
通过计算均值和方差的方式,计算采样区域的正态分布。
均值可以利用mipmap获得均值,利用平方的期望-期望的平方计算方差。
VSSM用的是切比雪夫,而不是正态分布。
步骤
- 生成depth map的同时生成square depth map。
- 计算遮挡物的平均深度。可以通过mipmap获得整个区域的平均深度,但是要计算的是遮挡物的平均深度。
N 1 / N N_1/N N1/N:切比雪夫
N 2 / N N_2/N N2/N:1-切比雪夫
z u n o c c z_{unocc} zunocc:着色点的深度。

问题:如果切比雪夫近似失败会产生light leaky问题,导致部分阴影错误变亮。
Moment Shadow Mapping
多加几项,使用不同的矩进行更精确的近似。
问题:如何根据前4阶的矩,得出近似函数?

VSSM实际上就是用了前2阶的矩。
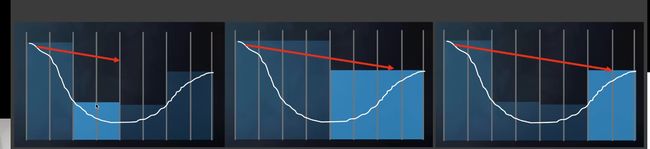
7 Distance field shadow
SDF的应用
-
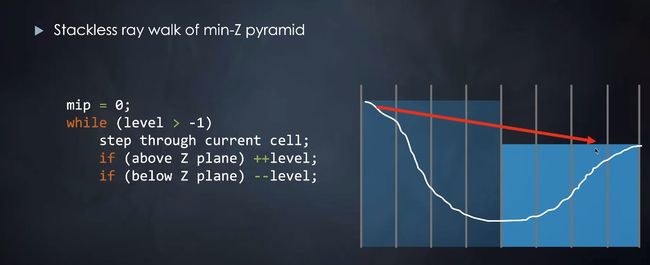
加速ray marching
安全距离,查询一个点的sdf,在这个半径内就可以放心ray marching。

-
生成软阴影。
安全角度:角度越小阴影越黑。

沿着边缘找最小的安全角度。
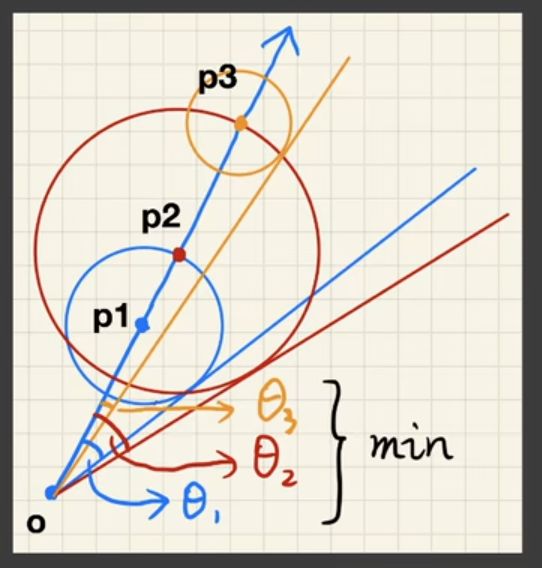
为了避免反三角函数计算,使用以下近似:

k可以用来控制软阴影程度。k越大越硬。
Real-time Environment Mapping
1 The Split Sum
1. 计算入射光的积分:prefilter the environment

不同的材质有不同的brdf,glossy的材质采样角度小,越镜面,较为集中,diffuse的材质采样均匀。可以体现为不同filter size过滤的environment map。
这样只需要根据材质在不同filter过滤后的环境贴图在镜面反射方向上采样一次就可以了。
2. 计算brdf的积分:

假设是微表面模型。
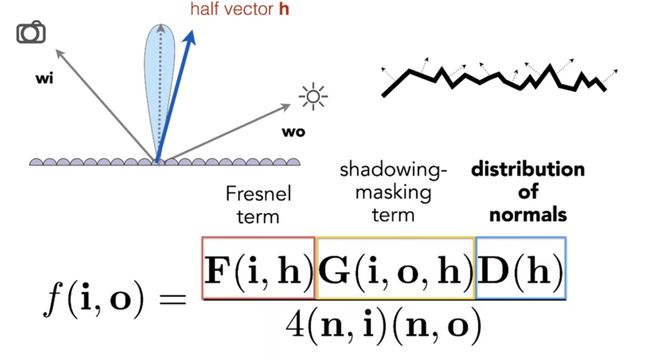

有三个变量需要考虑,需要进行三维的预计算。
把fresnel项代入渲染方程中,将 R 0 R_0 R0移到积分外面。
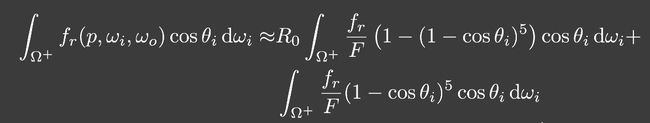
把后面的两个积分烘焙成两张纹理(2个通道),就避免了采样。
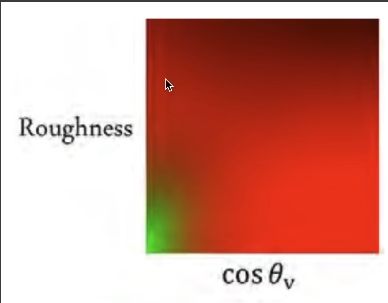
2 Spherical Harmonics
定义在球面上的一系列二维的基函数

每一阶有2l+1个基函数。范围是[-l,l]。前n阶有 n 2 n^2 n2个基函数。适用于分析球面上的性质。
Legendre多项式来计算基函数。
可以用SH来描述光照和BRDF,适合用于描述低频光照(前3阶)。
Spherical harmonics的性质
- orthonormal
- simple projection(把要投影的函数做乘积)/reconstruction
- simple rotation(旋转每个基函数相同的角度,任意的旋转都可以被同阶基函数的线性组合得到)
- simple convolution
- few basic functions: low freqs
SH只适合描述低频的函数。
3 得到环境光照下的阴影
3.1 解决方案1
选最重要的几个光源(比如太阳),生成阴影。
3.2 在环境光照下的渲染

最复杂的方法:每个shading point,存储3张贴图。

PRT
precompute lighting and lighting transport.
基本思想:假设场景中只有光照变化,把可见性和brdf都固定住。
渲染方程分为lighting和light transport两部分,把lighting拆成basis function。
假设场景中所有东西都不变,除了lighting,light transport对于每个点是固定的东西。
使用的工具:spherical harmonics
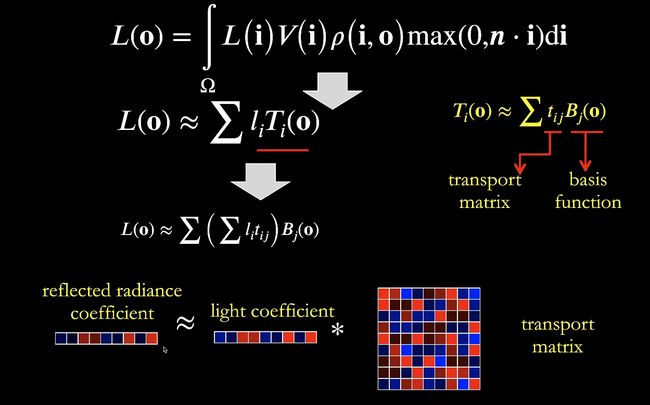
Diffuse Case
先把光照描述成Spherical Harmonics
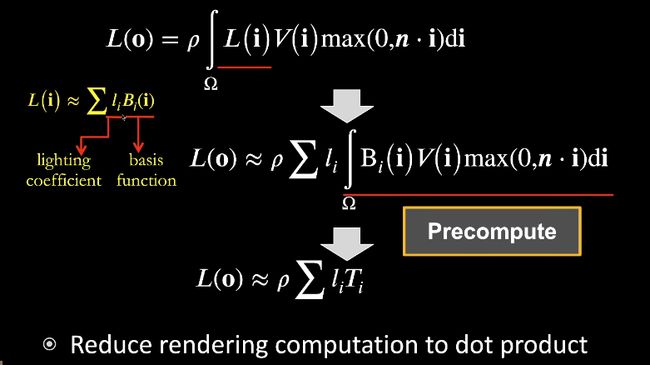
假设diffuse材质,即brdf常数,也可以写成以下形式:
Glossy Case
brdf不再是常数,每一个o给一组vector。从向量点乘向量变成向量点乘矩阵。
缺点
- 要求是静态场景,只能做光源。
- 存储和读取会产生负担。
Real-time Global Illumination
Reflective Shadow Maps(RSM)
次级光源: 认为所有的反射物(次级光源)是diffuse的。
怎么使用次级光源

f r = ρ / π f_r = \rho / \pi fr=ρ/π是点q的brdf。
L i = f r ⋅ Φ d A L_i = f_r \cdot \frac{\Phi}{dA} Li=fr⋅dAΦ是对于点p而言的。出射的radiance乘以入射的irradiance。
1.不考虑遮挡问题。
2.4次方的原因是还要进行归一化。
注意事项
对每个着色点,只需要寻找足够近的次级光源。
采样技巧
那既然世界坐标比较接近不好找,那么就用shadow map的距离进行近似,假设shadow map的采样近,就是在世界坐标中距离近。

缺点
一个光源一个shadowmap
不计算反射物到shading point的可见性。
假设:diffuse reflectors、depth as distance。
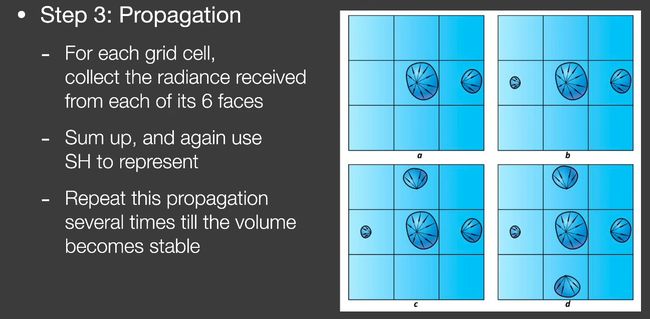
Light Propagation Volumes(LPV)
思想:radiance在传播的过程中不会改变。
把场景分成格子,查询每个格子接收的radiance。
步骤
-
哪些点可以作为次级光源?
RSM找到次级光源。 -
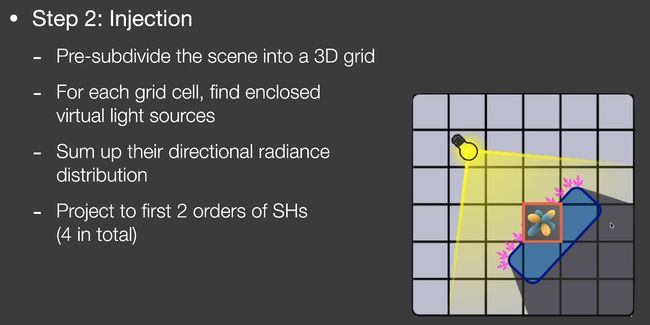
将光注入到格子中(计算初始值)。
把场景划分成三维的格子(三维纹理)。
格子内部的所有虚拟光源相加。
得知空间上每个格子的radiance分布,投影到2阶的SH上。
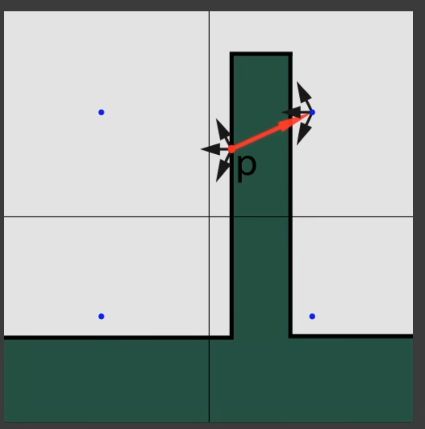
-
通过格子渲染
找到着色点位于的格子
获取格子中所有的incident radiance,然后着色。
问题:light leaking,应该被照亮的和不该被照亮的在一个格子里(可以用自适应方法,cascade)。
Voxel Global Illumination(VXGI)
也是2-pass。
把次级光源变成体素。(pixel->voxel)
第二个pass的时候,对每个shading point做cone tracing(每个像素做一遍)。
把整个场景划分成格子,然后划分层级,建立一棵树。
pass from light(决定哪些patch会被照亮)
记录的不是出射的半球形分布,而是记录incident lighting的分布(光从哪来)与法线分布。
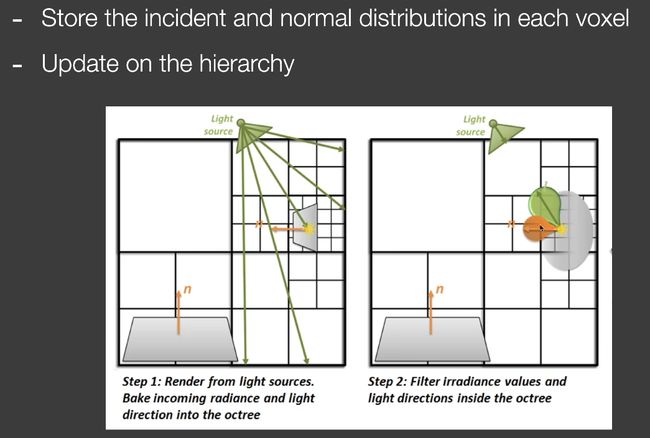
通过这种方法,就可以根据不同的材质计算不同的出射分布。
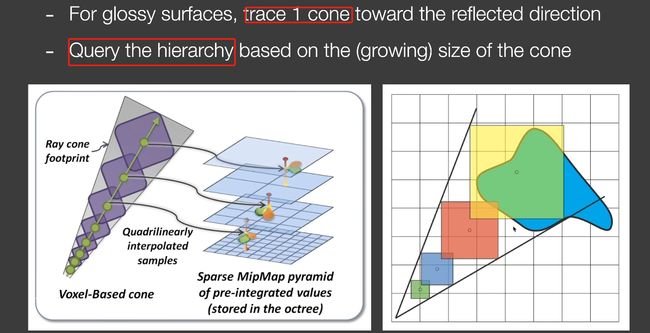
pass from camera
cone-tracing:不必计算cone经过的所有体素,因为圆锥越来越大,所以在hierarchy上找到对应的层级进行采样。
这样就不用每次都查最小纹素了。
注意事项
Screen Space Ambient Occlusion(SSAO)
特点
- 是对全局光照的近似。
- 在屏幕空间
主要思想
AO部分
蓝色的部分可以理解成平均。
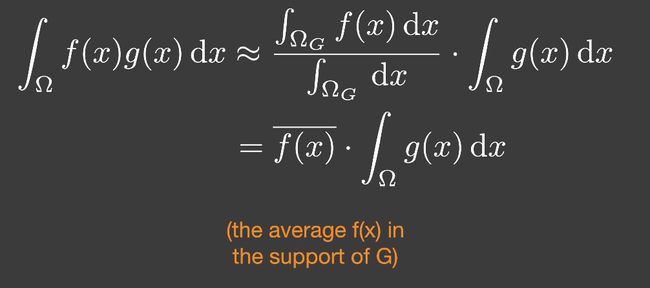
g(x)的积分是个常数,diffuse,间接光照都是常数。
其实可以直接把常数拿出来,入射光是常数,brdf是diffuse的。

SS部分
选定半圆半径R,在半圆内进行trace。SSAO在球里面撒点,在物体内部表示看不见,物体外部看的见。
把撒的点和投影到camera与深度缓存做比较。
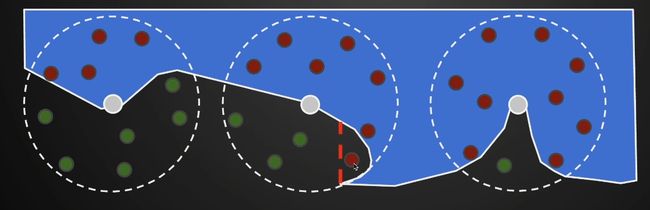
缺陷就是凹几何体。
红点过半才会考虑AO问题。
可以用少量的采样得到有噪声的结果,然后再滤波。
也可以根据法线只算半球,法线也可以进行cos加权(加权以后就是HBAO,可以避免凡是遮挡就变暗的问题)。
Screen Space Directional Occlusion SSDO
不必认为着色点接收到的所有入射光照都是一样的。
次级光源不来源于RSM,而是来自于相机。
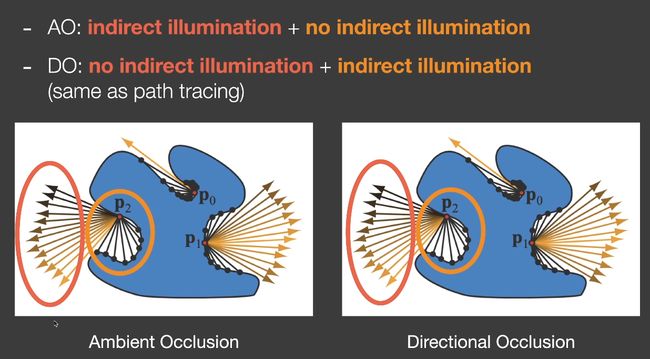
SSAO和SSDO的比较
采样方式和HBAO相同,都是在法线方向的半球采样。但是只有被挡住的点才会提供间接光照(右图中的ABD)。

和SSAO一样,不计算从P到A能否被挡住,而是camera到A能否被挡住。
缺陷:因为是在相机位置计算是否遮挡,所以从p点本来应该当作次级光源的点可能不被计入。
Screen Space Reflection(SSR)
可以在屏幕空间上做光线追踪。
考虑任何光线和从相机罩过去的"壳"求交。
改进
- 采样改进(重要性采样)
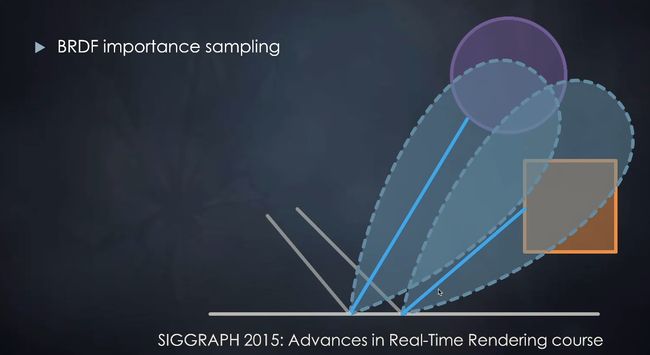
- 复用采样信息(tracing的两条光线可以给别的着色点复用,计算该着色点对另一个点间接光照影响)
- 对于glossy的物体,可以对屏幕空间进行模糊,然后镜面方向采样(但是要考虑深度的差异)。
问题:diffuse采样过多 、只局限于屏幕空间。
Physically-based Material(surface models)
Cook-Torrance reflectance equation
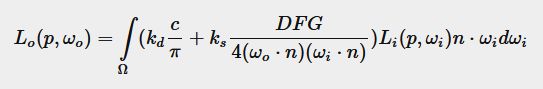
左边是Lambert漫反射模型。
F:菲涅尔项,反射的比例(垂直反射的更多)。
K s K_s Ks:高光的比例。
K d K_d Kd:漫反射的比例。
Normal distribution function(NDF)
法线分布函数是二维的,描述微平面与半程向量对齐的量。越粗糙越不对齐,光线越发散。
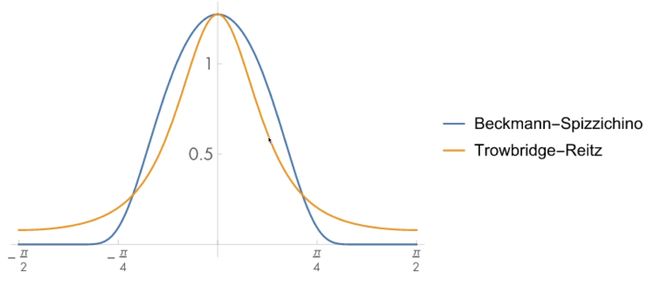
Beckmann NDF
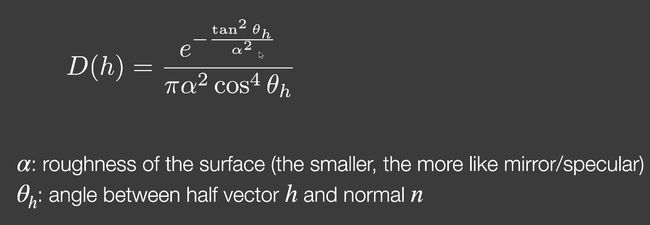
GGX(long tail,边缘会有一种diffuse的感觉)和beckman的对比。
Geometry function
避免在grazing angle时非常亮。
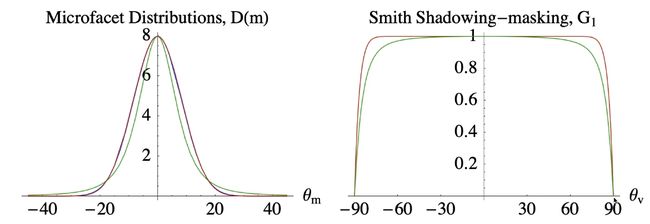
拆开shadowing和masking项,描述自遮挡(越和表面垂直越不遮挡)。
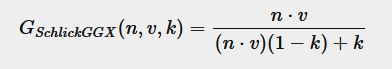

观察方向和光照方向都考虑:
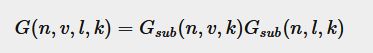

Fresnel equation
导体和绝缘体反射的曲线是不同的。
解决能量不守恒问题
Kulla-Conty:补充多次反射损失的能量。
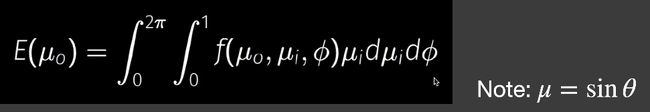
上式是半球面的积分, L i = 1 L_i=1 Li=1,f是微表面模型的brdf。
通过上式,得出能量损失: 1 − E ( μ o ) 1-E(\mu_o) 1−E(μo)。
为了计算 2 ∫ 0 1 E ( μ i ) μ i d μ i 2\int^{1}_{0}E({\mu}_i){\mu}_id{\mu}_i 2∫01E(μi)μidμi,需要预计算。打表的变量是 μ \mu μ和roughness。
BRDF有颜色怎么办:考虑菲涅尔项 F F F。
颜色就相当于能量损失,所以先通过菲涅尔项计算有多少能量被反射了。
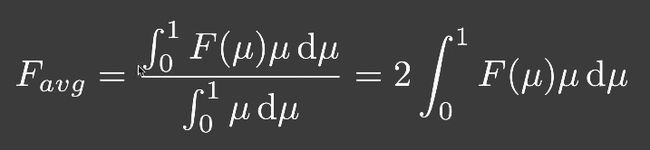
所以,反射给人眼的能量是 F a v g E a v g F_{avg}E_{avg} FavgEavg。考虑多次弹射,有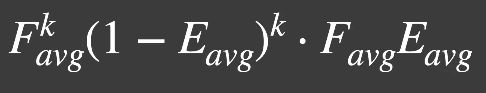
把所有项加起来,得到颜色项:
考虑颜色能量损失的版本是没颜色的版本乘以颜色项。
Linearly Transformed Cosines线性变换余弦(LTC)
(多边形光源情况下)用于解决microfacet models的着色问题。
将2D的BRDF lobe转化成余弦,光源的形状也一起跟着变化,在变换后的光源上进行积分是有解析解的。
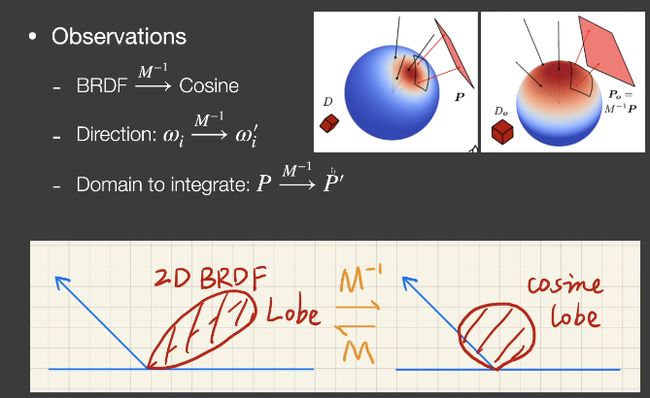

假设 L i L_i Li是均匀的, ω i \omega_i ωi是原来的方向,$\omega_i’是变换过的方向。
Disney Principal BRDF
不一定是物理正确的,但易于艺术家理解。
具有强大的表现能力。
通过拟合来计算。
参数空间太大。

PBR材质的缺点
微表面模型不擅长表示真实的模型。
不利于美术理解。
Non-Photorealistic Rendering(NPR)
风格化渲染:fast and reliable stylization
Outline Rendering
什么是边?
边界、折痕、材质边界、轮廓(多个面共享的才是Sihouette)

shading 方法做描边
法线法: 观察的方向和法线几乎垂直的着色点,就是Sihouette边。
角度可以选不同的threshold。
扩大法: 可以直接用背面来描边,把背面扩大了以后渲染。
用图像的方法描边
方法很灵活,也可以对法线、深度找边缘。
Color blocks
对着色结果阈值化或量化(可以划分许多色阶,比如2(阈值化)、255(量化))。

Strokes Surface Stylization
- 分析不同的点应该用哪种密度。
- 每个点的笔触应该连续(可以预制好纹理)。

每一级有不同的密度(采样的时候对相邻位置不同密度的纹理进行采样),对每个固定密度的图做mipmap,mipmap密度不变。
Real-time Raytracing
SPP:sample per pixel

primary可以替换成rasterization,所以光线少了。
RTRT的关键技术:Denoising
目标1. Quality(如果滤波太重了会有overblur,no artifac,keep all details)
- Speed(<2/5ms to denoise one frame)
工业界的解决方案
- Temporal:在时间上进行滤波,认为前一帧是滤波好的,不会发生突变,重用前一帧。
- motion vector来寻找之前的位置。
- 变相的增加了SPP。
- 在空间上的做法。
The G-Buffers
Geometry buffer 几何缓冲区,保存屏幕空间的信息。
Back Projection
找当前帧的像素x在上一帧的位置,计算准确的motion vector。
- 找到当前帧此像素的世界坐标s(从G-buffer取,或通过 s = M − 1 V − 1 P − 1 E − 1 x s=M^{-1}V^{-1}P^{-1}E^{-1}x s=M−1V−1P−1E−1x计算)。
- 运动是知道的,可以知道上一帧的世界坐标, s ′ = T − 1 s s^{'}=T^{-1}s s′=T−1s
- 可以计算上一帧的屏幕位置, x ′ = E ′ P ′ V ′ M ′ s ′ x' = E'P'V'M's' x′=E′P′V′M′s′
降噪过程
当前帧在空间上先自己降噪,然后与上一帧对应的像素进行线性混合。
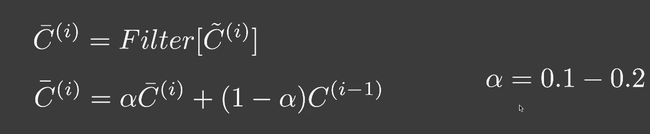
Temporal失败的场景
-
切换场景、光源突变
-
在走廊里倒退着走(新出现的像素在上一帧中找不到对应位置)
-
光源在移动的时候,motion vector不变(motion vector是相机计算的),会产生shadow detach问题。
-
glossy反射时,反射要等一会才能移动到正确的位置。
解决方法
- Clamping:首先将上一帧拉近到当前帧相似的结果,然后再混合。
- Detection:用object ID来检测对应点是否再同一个物体上。调整 α \alpha α(但是结果会更noisy,重新引入了噪声,可以增加空间上的采样范围)。
滤波的实现
一般是低通滤波(移除高频信号)。
高斯滤波
在 μ \mu μ周围取3 σ \sigma σ的半径就够了,因为太远的贡献太小。
高斯滤波也会把边界模糊掉,但是希望把边界保留。所以引入了双边滤波。
1个标准:像素之间的距离
Bilateral filtering 双边滤波
边界:非常剧烈的颜色改变。
比较像素i和像素j,如果像素差异太大,那就不让j的像素颜色贡献到i上。

2个标准:像素之间的距离、颜色的差距
Joint Bilateral Filtering
联合不同的特征,适用于路径追踪产生的噪声。
Unique advantages in rendering
- A lot of free “features” known as G-buffers.
- Normal, depth, position, object ID, etc.,mostly geometric
G-Buffer还是noise-free的。
比如下图,AB之间用深度做特征较好,BC之间用法线做特征较好。DE用颜色之间的差异更好。
filter的加速方法
Separate Passes
水平filter一边,竖直filter一遍。
高斯函数的x和y是可以拆分的。

但是双边滤波就不能这样实现了,因为它们不能拆分,但有时也可以强行拆分(卷积核大小小于32)。
Progressively Growing Sizes
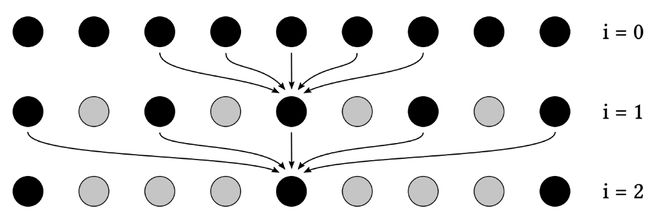
逐步增大的filter多次滤波(a-trous wavelet)
为什么可以这么做?
- 为什么size逐渐变大?
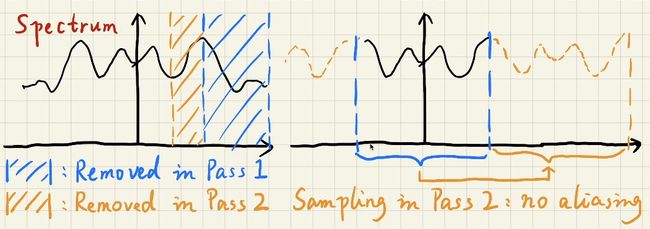
更大的filter意味着要去除更低的频率。 - 为什么可以跳过样本?
Sampling == repeating the spectrum(频谱)
Outlier Removal
有时图像会有outlier(超级亮的像素),滤波会产生更大的噪声,因此要在滤波前去除outlier。
- 对每个像素,取7x7的像素,计算均值和方差。
- 所有的之应该在 [ μ − k σ , μ + k σ ] [\mu - k \sigma,\mu + k \sigma] [μ−kσ,μ+kσ],不在的就是outlier。
- 对于outlier,clamp到上述的范围。
Temporal Clamping
在当前帧的点采样,获得均值和方差,将上一帧noise free的结果clamp到 [ μ − k σ , μ + k σ ] [\mu - k \sigma,\mu + k \sigma] [μ−kσ,μ+kσ]范围。
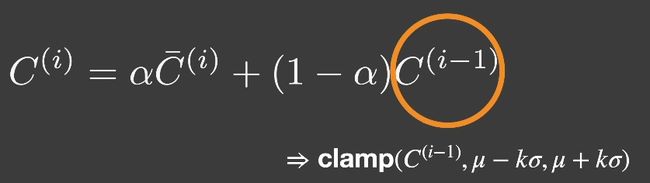
SVGF - Spatiotemporal Variance-Guided Filtering
Joint Bilateral Filtering: 3 factor3 to guide filtering
Depth

A和B理应彼此贡献,权重大。
所以不是直接用相机出发的深度,而是用在在切平面上的深度。
Normal
法线使用点积来赋予权重, σ n \sigma_n σn控制衰减的速度。
不使用法线贴图变换过的法线。

Luminance
噪声会让噪声有干扰,所以不能直接根据颜色的差异赋予权重。
所以要计算方差,先spacial,再temporal(时间上累计),再spacial。得到相对平滑的variance值。

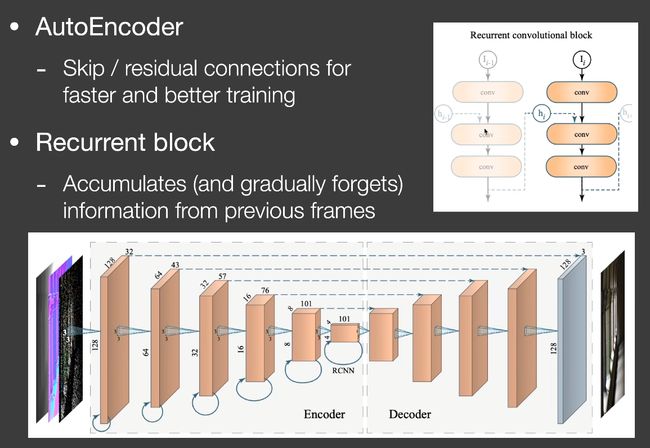
RAE - Recurrent denoising AutoEncoder
- 用Recurrent AutoEncoder的结构对RTRT进行滤波(后期处理,输入是有噪声的图,输出是没有噪声的图)。
- 网络自动执行temporal accumulation。
Key architecture design
- AutoEncoder(or U-Net) structure
- Recurrent convolutional block
低频噪声是boiling artifact
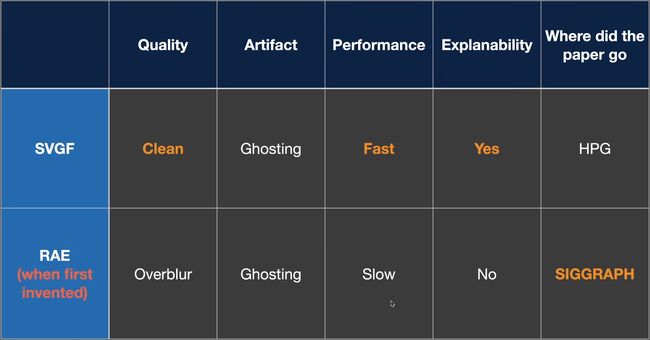
比较
工业界的一些解决方案
Temporal Anti-Aliasing(TAA)
走样的原因:采样的数量不足。
解决方案:用更多的样本(MSAA)
思想:当前这一帧复用上一帧的sample,当前帧还用一个spp。
TAA使用jittering sampling。

每一帧像素内部的采样点周期性改变(每一帧用不同颜色的点)。
SSAA(supersampling) vs MSAA(Multisample)
SSAA:在一个更大的分辨率渲染,然后降采样。开销很大。
MSAA:对于同一个primitive,所有的样本只做一次sampling。在空间上可以做sample reuse(比如在边界上采样,边界上一个点当两个点用,下图就是6个点当8个点)。
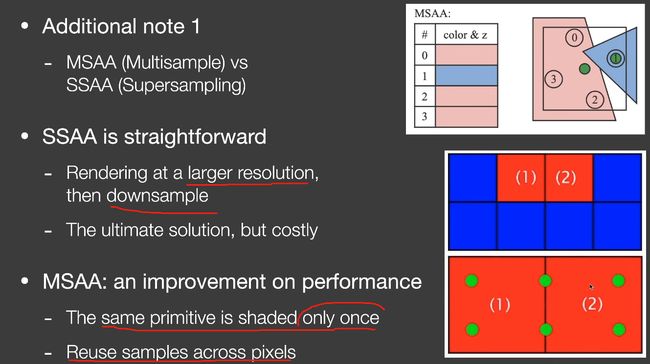
Image based anti-aliasing solution
先渲染出有锯齿的图,然后用无锯齿的替换有锯齿的。
FXAA->MLAA(Morphological AA)->SMAA(Enhanced subpixel morphological AA)
上面是矢量化的思想(SMAA)。
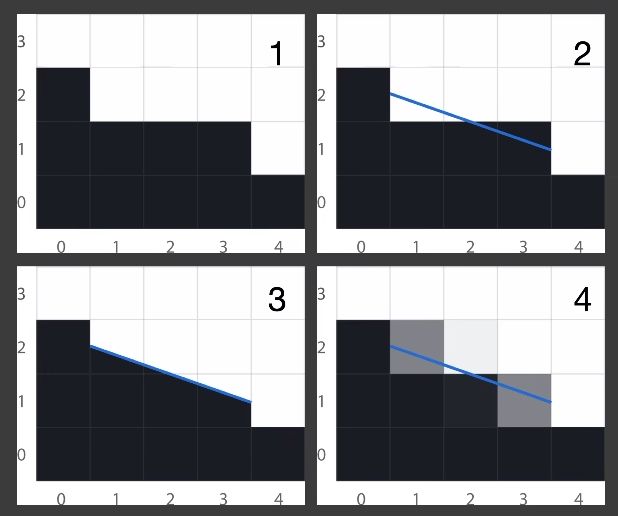
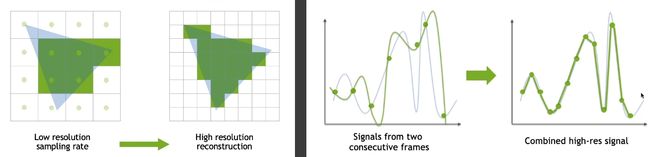
Temporal Super Resolution
超分辨率,单独训练一个识别边缘的神经网络。
- DLSS 1.0:全靠猜。
- DLSS 2.0:利用temporal信息填到这一帧。
因为分辨率增加了,不能直接重用,增加了采样点,但是要寻找更好的复用上一帧的方案。
DLSS解决了如何使用temporal信息的问题。
Deferred Shading
节省Shading时间的方法。
原始光栅化流程的复杂度是O(fragment*light)。
Deferred Shading只着色可见的fragment。
步骤
- Pass 1: 不着色,只更新深度缓存。
- Pass 2:再做一遍光栅化(只有严格等于Pass1深度缓存的片元着色)。
- rasterize一遍场景开销比对所有不可见fragment着色开销小。
问题
- 难做anti-aliasing,可以用TAA和image based AA。
Tiled Shading
把屏幕分成32x32的tile,然后对每个tile进行shading。
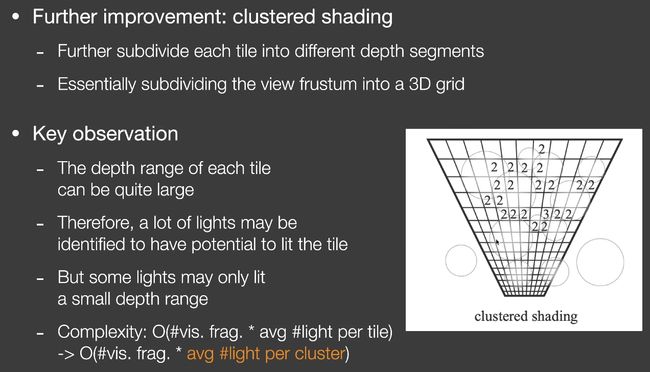
Cluster Shading
在tile的标准上进一步划分成不同的depth segments。
Level of Detail Solutions
key challenge
- Transition between different levels
- Usually need some overlapping and blending near boundaries.
Lumen
hybrid solution
- 先做一遍SSR,得到近似的GI。
- Upon SSR failure,使用更复杂的光线追踪。
加粗的部分就是UE5 Lumen的实现。
Software ray tracing
SDF相较于BVH树的三角形更有利于求交。适合在GPU中求交。
- HQ SDF for individual objects that are closed-by.
- LQ SDF for the entire scene.(远处的object用低质量的SDF)
- RSM if there are strong directional/point lights.
- Probes that stores irradiance in a 3D grid.
Hardware ray tracing
- 用简化的模型代替原始的模型。
- Probes