算法搜索（2024/2/5）

搜索 

目录

搜索 

深度优先搜索 

广度优先搜索  （宽度优先搜索）

今日刷题  

p1387 最大正方形

题目描述

输入格式

输出格式

输入输出样例

---

1、定义：

搜索是一种通过穷举所以可能的解的状态，来求得题目所需求的解或最优解的方法。

【即通过枚举解的所有可能状态，来寻求一个解或者最优解】

【状态】对某一系统在某一时刻的数学描述。

【状态转移】从一种状态转化为另一种状态。

2.分类：

深度优先搜索（dfs）和  广度优先搜索（bfs）

深度优先搜索：

广度优先搜索：

【注意】序号顺序代表遍历顺序！！

深度优先搜索 

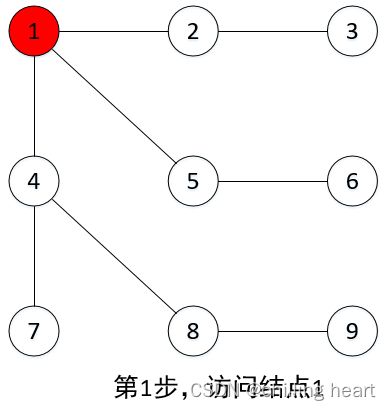
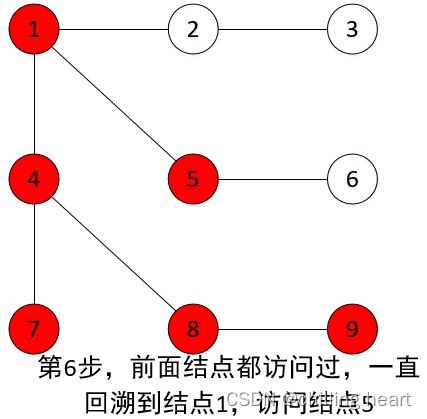
1、算法核心：沿着树的深度遍历树的结点，尽可能深的搜索树的分支。当结点v的所有边都已经遍历过来，搜索将回溯到发现结点v的那条边的起始结点。这一过程一直进行到已经发现从源结点可达到的所有结点为止。如果还存在未被发现的结点，则选择其中一个作为源结点并重复以上过程，整个过程反复进行直到所有结点都被遍历为止。属于盲目搜索。

2、基本原则：按照某种条件往前试探搜索，如果前进中遭到失败，则退回另选择道路继续搜索，直到找到满足条件的目标位置。

我找了一个清晰的图作为解释说明：

代码实现：

int dxy[4][2]={//模拟上下左右四个方向
	-1,0,    //上（x减一，y不变）
	1, 0,    //下
	0,-1,    //左
	0, 1     //右
	}
void dfs(int x0,int y0)
{
	if(x0,y0满足某种条件)     //找到目标点
	{
		                     //执行操作如输出路径等
		return；
	}
	for(int i=0;i<4;i++)     //遍历四个方向每一个分支，对每一个分支都进行深度搜索
	{
		int dx=dxy[i][0];   //移动后的横坐标
		int dy=dxy[i][1];   //移动后的纵坐标
		if(坐标越界||遇到障碍物||...)     //不满足条件
			continue;
		                                //执行操作
		dfs(dx,dy)                     //深度遍历
		                              //遍历结束恢复操作
	}
}

广度优先搜索  （宽度优先搜索）

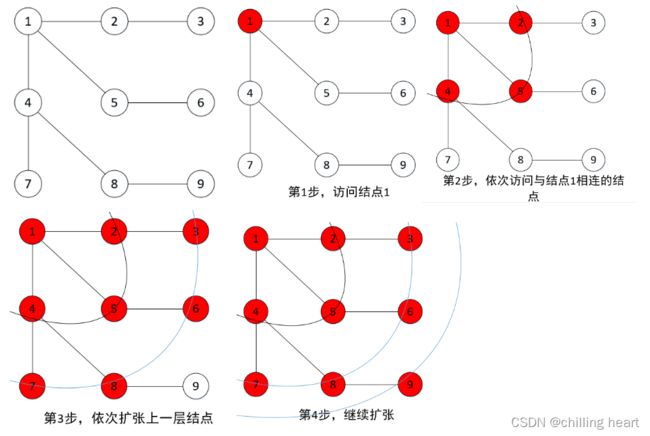
1、算法核心：每次都尝试访问同一层的结点，如果同一层都访问完了，再访问下一层，这样做结果是bfs算法找到的路径是从起始结点开始的最短合法路径（即这条路径包含的边数最小）。

图解：

代码实现：

static const int dirs[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
void bfs(int row, int col) 
{
    if (row,col满足某种条件) 
    {
        return;
    }
    int * queue = (int *)malloc(sizeof(int) * m * n);
    int head = 0;
    int tail = 0;                          //  双指针实现队列先进先出
    queue[tail++] = row * n + col; 
    while (head != tail)
    {
        int row = queue[head] / n;
        int col = queue[head] % n;
        head++;
        for (int i = 0; i < 4; i++) 
        {
            int newRow = row + dirs[i][0], newCol = col + dirs[i][1];
            if 满足某种条件(newRow >= 0 && newRow < m && newCol >= 0 && newCol < n &&……) 
            {
                对点进行某种操作操作
                queue[tail++] = newRow * n + newCol;
            }
        }
    }
    free(queue);
}

今日刷题  

p1387 最大正方形

题目描述

在一个 n×m 的只包含 0 和 1 的矩阵里找出一个不包含 0 的最大正方形，输出边长。

输入格式

输入文件第一行为两个整数 n,m(1≤n,m≤100)，接下来 n 行，每行 m 个数字，用空格隔开，0 或 1。

输出格式

一个整数，最大正方形的边长。

输入输出样例

输入 

4 4
0 1 1 1
1 1 1 0
0 1 1 0
1 1 0 1

输出 

2

思路：

1.以【i，j】为正方形的左上角，使用广搜遍历直到遇到0为止。

2.bfs遍历：遍历（x+1，y）、（x，y+1）、（x+1，y+1）；因为广搜具有层次性，所以能保证1~l长度的正方形都能依次遍历。

AC代码如下：

#include 
#include 
#include 
#include 

using namespace std;
int n, m,f[310][310];
int a[310][310];
int main()
{
    scanf("%d %d", &n,&m);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
    int ans = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            if (a[i][j] == 1)
                f[i][j] = min(f[i][j - 1], min(f[i - 1][j], f[i - 1][j - 1])) + 1;
            ans = max(f[i][j],ans);
        }
    printf("%d\n",ans);

    
    return 0;
}

祝大家有所收获！！