python_ACM模式《剑指offer刷题》二叉树2

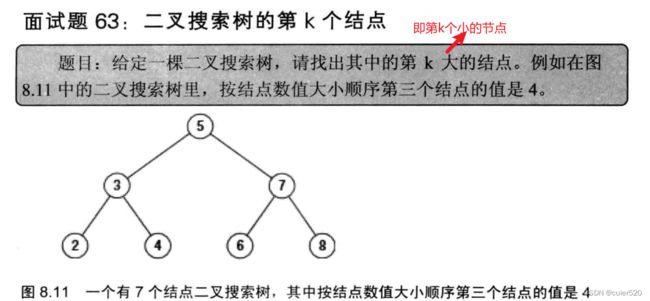
题目：

面试tips：

面试官有可能问到：

如果你需要频繁地查找第 k 小的值，你将如何优化算法？（见思路三）

思路：

思路一：二叉搜索树最大的特点就是中序遍历是递增的。因此最容易想到的是对二叉树进行中序遍历存入数组中，再遍历数组至第k个数，就是二叉树的第k小的数/节点。这样的时间复杂度就是O(N+K),空复为O(N)。显然不是最优。

思路二：在思路一的基础上不采用数组，直接对二叉搜索树进行中序遍历，在遍历的过程中目标是找到第k个小的节点。此时因为是中序要先遍历到最左节点后再退回遍历k个，因此最理想(即二叉搜索树为平衡二叉树)的时复为O(logN+K),最不理想(此二叉搜索树没有右子树)才达到O(N+K)，此方法需要用到栈或递归（因为其遍历到的节点并不处理，它要遍历到最左节点再从最左节点开始处理，是一个后进先出的处理思想）因此需要用到递归或栈，因此空复最理想为O(logN)，最不理想为O(N). 已经比思路一好很多了。

思路三：虽然思路二已经好很多，且觉得应付大部分面试应该没问题。但如果需要频繁查找第k小的值，要如何优化？（这是从leetcode上看来的）觉得有点意思。这个思路是如果能知道以node为根节点的子树有多少个节点(假设存为了一个字典node_count)，则起初node = root。如果node_count[node] < k-1, 则等价于找node.right的第k - (left + 1)个节点；如果node_count[node] == k-1, 则node即为第k个节点；如果node_count[node] > k-1, 则等价于找node.left的第k个节点，一直下去直至找到为止。显然这里就需要预处理node_count，遍历整颗二叉搜索树，统计以每个节点node为根节点的子树的节点个数存入字典中，时复O(N), 空复O(N). 后多次查询第k小的节点时时复最理解为O(logN),最不理想为O(N).

代码实现：

思路一略

思路二的迭代法：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def arr2tree(arr, index):
    # 满二叉树数组格式构造二叉树
    # 构造arr[index]的二叉树
    # 满二叉树数组格式: 是指首先按层序遍历顺序，且二叉树的非空节点的左右孩子(尽管为空)都会打印出来，空节点的左右孩子则不打印
    if index >= len(arr) or arr[index] == None:
        return None
    root = TreeNode(val = arr[index])
    left = arr2tree(arr, 2 * index + 1)
    right = arr2tree(arr, 2 * index + 2)
    root.left = left
    root.right = right
    return root

class Solution:
    def kthSmallest(self, root, k) :
        # 刚才中序遍历递归法查找
        # 现用中序遍历的迭代法查找第k小的数
        # 题中说明没有非空的情况 因此不对非空进行处理
        stack = [root]
        while stack:
            node = stack.pop()
            if node:
                # 如果不是空 说明第一次遍历至此，用None标记是第二次遍历到此时才开始处理
                # 中序 为左中右，因此存入栈中是右中左
                if node.right:
                    stack.append(node.right)
                stack.append(node)
                stack.append(None)
                if node.left:
                    stack.append(node.left)
            else:
                node = stack.pop()
                # 每遇到一个None时 说明这个节点被遍历第二次了 即开始处理了
                k -= 1
                if k == 0:
                    return node.val

if __name__ == '__main__':
    arr = [5, 3, 6, 2, 4, None, None, 1]
    k = 3
    root = arr2tree(arr, 0)
    a = Solution()
    print(a.kthSmallest(root, k))  # 3

思路二的递归法：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def arr2tree(arr, index):
    # 满二叉树数组格式构造二叉树
    # 构造arr[index]的二叉树
    # 满二叉树数组格式: 是指首先按层序遍历顺序，且二叉树的非空节点的左右孩子(尽管为空)都会打印出来，空节点的左右孩子则不打印
    if index >= len(arr) or arr[index] == None:
        return None
    root = TreeNode(val = arr[index])
    left = arr2tree(arr, 2 * index + 1)
    right = arr2tree(arr, 2 * index + 2)
    root.left = left
    root.right = right
    return root

class Solution:
    def __init__(self):
        # 初始化全局变量，这里让self.k作为全局变量是想找整棵树上第k小的数
        self.k = -1
        self.result = -1

    def kthSmallest(self, root, k: int):
        # 直接在二叉树中找第k小的元素
        def dfs(root):
            # 找以root为根节点的第k小的数，找到就【更新】self.result并返回，此函数只需更新因此不用返回值
            # 终止条件
            if not root:
                return
            # 单层
            dfs(root.left)
            self.k -= 1
            if self.k == 0:
                self.result = root.val
            dfs(root.right)
        self.k = k
        dfs(root)
        return self.result

if __name__ == '__main__':
    arr = [5, 3, 6, 2, 4, None, None, 1]
    k = 3
    root = arr2tree(arr, 0)
    a = Solution()
    print(a.kthSmallest(root, k))

思路三：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def arr2tree(arr, index):
    # 满二叉树数组格式构造二叉树
    # 构造arr[index]的二叉树
    # 满二叉树数组格式: 是指首先按层序遍历顺序，且二叉树的非空节点的左右孩子(尽管为空)都会打印出来，空节点的左右孩子则不打印
    if index >= len(arr) or arr[index] == None:
        return None
    root = TreeNode(val = arr[index])
    left = arr2tree(arr, 2 * index + 1)
    right = arr2tree(arr, 2 * index + 2)
    root.left = left
    root.right = right
    return root

class pre_do:
    def __init__(self, root):
        self.root = root
        self.count_node = {}
        self.cal_count_node(root)

    def cal_count_node(self, node):
        # 得到预处理好的self.count_node字典--后序遍历
        # 统计以子树中某个节点 为根节点的子树的节点个数
        # 注意这里如果node为空是不会被存到字典中，因此后面get时要对空作特殊处理
        if not node:
            return 0
        self.count_node[node] = 1 + self.cal_count_node(node.left) + self.cal_count_node(node.right)
        return self.count_node[node]

    def get_count_node(self, node):
        return self.count_node[node] if node else 0

    def find_kthSmallest(self, k):
        node = self.root
        while node:
            left_count = self.get_count_node(node.left)
            if left_count < k - 1:
                node = node.right
                k -= left_count + 1
            elif left_count == k - 1:
                return node.val
            else:
                node = node.left


class Solution:
    def kthSmallest(self, root, k: int) -> int:
        result = pre_do(root)
        return result.find_kthSmallest(k)

if __name__ == '__main__':
    arr = [5, 3, 6, 2, 4, None, None, 1]
    k = 3
    root = arr2tree(arr, 0)
    a = Solution()
    print(a.kthSmallest(root, k))  # 3

参考资料：

1. 《剑指offer》

2. 力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台