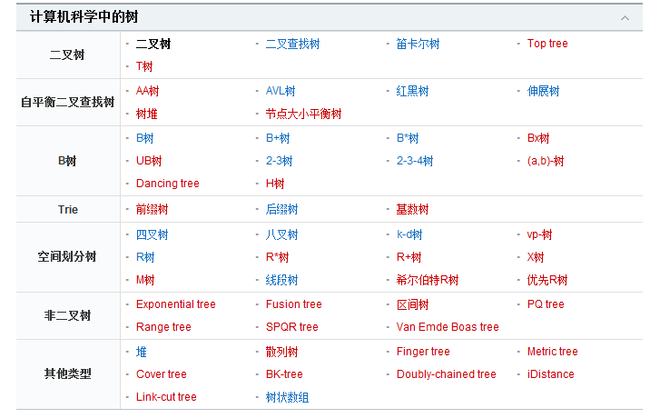
单词查找树
单词 查找树:高级数据结构的第一个
经验:
1、在博客中加入网络链接、论文链接,对一个数据结构本身及其本质,极其变形有一个全面的了解
2、对于从来没写过的数据结构和算法:第一遍参考别人的代码快速写出是一种高效率的方法,可以变通一下,不要再一个从来未接触过的东西上试图自己想出来,
太耗时间。
参考论文:
http://d.wanfangdata.com.cn/Periodical_jsjgcykx201004032.aspx
http://www.cnblogs.com/tanky_woo/archive/2011/06/08/2075613.html
参考文献:
http://www.cnblogs.com/tanky_woo/archive/2010/09/24/1833717.html
http://www.cnblogs.com/rollenholt/archive/2012/04/24/2468932.html
http://www.cppblog.com/yuyang7/archive/2009/03/27/78083.html
http://609866532-qq-com.iteye.com/blog/1176958
http://blog.csdn.net/ts173383201/article/details/7858598#
深入研究问题,提高水平,在第二阶段的时候要学习这个哥们学习的方法:
http://blog.csdn.net/v_july_v/article/details/6897097 尤其是最后关于,深入探索C++对象模型 的论述,以及对该数据结构和算法研究的深度和方法值得借鉴采纳
http://www.cppblog.com/hunter/archive/2011/09/30/67039.html
http://www.cppblog.com/abilitytao/archive/2013/04/22/80598.html
http://ds.fzu.edu.cn/fine/resources/articleContent.asp?id=346
http://www.pin5i.com/showtopic-27125.html 这个程序写的不错,值得借鉴
http://acm.nyist.net/JudgeOnline/articles/
学习到的方法:
1、深入研究,加深理论修养
2、比较高级和复杂,难以理解的算法,多参考20篇博客,10篇论文,彻彻底底的搞清楚这个问题
3、看懂了自己写代码,或者先参考别人的代码,实现功能
4、研究高级的数据结构和算法,才能从中获得提高的途径,那些从前没有研究过或者没有勇气研究和实现都应该去研究,彻彻底底弄懂,写程序实现
5、talk is cheap,show me the code
计算机科学中的树:各种各样的树,应用广泛。
下面是我实现的字典树,这是我实现的一个中级要求的数据结构:
抽象数据类型定义:
//字典树结构体
struct TrieNode
{
int branches; //存放当前结点的分支数
TrieNode *tn[26]; //最多有26个字母
TrieNode() //当前结点的字符数初始化为0
{
branches=0;
for(int i=0;i<26;i++)
tn[i]=NULL;
}
};
//单词查找树类
class TrieTree
{
public:
//构造函数,析构函数
TrieTree()
{
tnr=NULL; //根结点初始化为空
}
~TrieTree(){}
//搜索、插入、删除、输出
bool SearchTrieTree(const char *c);
bool InsertTrieTree(const char *c); //插入的为字符串,所以应该是字符指针
private:
TrieNode *tnr; //单词查找树的根结点
};
/*
插入算法:(下面这些算法最终必须明白):用位置索引表示字母,巧妙
1、设置当前结点为根结点,设置当前字符为插入字符串中首个字符。
2、需要遍历这个字符串指针,直到结尾。
3、如果当前结点找不到匹配结点,则新建结点,将并将该字符赋值给它,当前结点字符数加1。
4、当前结点设置为新建的这个结点,然后循环处理插入问题。
*/
bool TrieTree::InsertTrieTree(const char *c)
{
int i=0;
int chtoindex; //用于将字母转换为下标
if(tnr==NULL)tnr=new TrieNode; //如果根结点为空,则新建一个结点
TrieNode *tn=tnr; //将新建结点初始化为根结点
while(c[i]!='\0'&&tn!=NULL) //*c为C风格字符串
{
//对输入的字符进行转换
if(c[i]>='a'&&c[i]<='z')chtoindex=c[i]-'a';//减去'a'正好转换为下标值,>=号
else return false;
if(tn->tn[chtoindex]==NULL) //如果字母对应的分支不存在
{
tn->tn[chtoindex]=new TrieNode; //chtoindex已经包含这个字母的信息
tn->branches++; //该结点分支数加1
}
//当前结点设置为该分支结点
tn=tn->tn[chtoindex];
i++;
}
return true;
}
/*
搜索算法:
1、在字典树搜索给定的字符串,若不完全匹配返回假。
2、若完全匹配,判断是否落在叶节点上,是返回真,否返回假。
*/
bool TrieTree::SearchTrieTree(const char *c)
{
int i=0; //用于遍历给定的字符串
int indextoch;
TrieNode *root=tnr; //定位给定的字典树
while(c[i]!='\0'&&root!=NULL)
{
if(c[i]>='a'&&c[i]<='z')indextoch=c[i]-'a';
else return false;
if(root->tn[indextoch]!=NULL)
{
root=root->tn[indextoch]; //移到下一个位置
}
else
{
return false;
}
i++; //单词前进一个位置
}
if(root->branches==0)
return true;
else
return false;
}
主程序:
//对我而言,是一个中级的数据结构,丰富高级的数据结构和算法
int _tmain(int argc, _TCHAR* argv[])
{
//编程经验:对于复杂的算法(例如:B树,B+树,单词查找树,红黑树),要多看几个博客,及其代码,反复研究,直到看懂为止
cout<<"----------单词查找树----------"<<endl;
//编程经验:直接开始写程序,不要过度准备,花在准备上。
//对于从来没写过的数据结构和算法:第一遍参考别人的代码快速写出是一种高效率的方法
TrieTree tt;
const char *str1,*str2,*str3;
str1="lichao";
str2="liuyinuo";
str3="upch";
tt.InsertTrieTree(str1);
tt.InsertTrieTree(str2);
tt.InsertTrieTree(str3);
tt.InsertTrieTree("iloveliuyinuoforever");
if(tt.SearchTrieTree("iloveliuyinuoforever"))
cout<<"在单词查找树中找到了 爱的宣言"<<endl;
else
{
cout<<"单词查找树中没有这个单词"<<endl;
}
if(tt.SearchTrieTree(str1))
cout<<"在单词查找树中找到了lichao"<<endl;
else
{
cout<<"单词查找树中没有这个单词"<<endl;
}
if(tt.SearchTrieTree("lich"))
cout<<"在单词查找树中找到了lichuo"<<endl;
else
{
cout<<"单词查找树中没有这个单词lich"<<endl;
}
if(tt.SearchTrieTree(str2))
cout<<"在单词查找树中找到了liuyinuo"<<endl;
else
{
cout<<"单词查找树中没有这个单词"<<endl;
}
if(tt.SearchTrieTree(str3))
cout<<"在单词查找树中找到了upc"<<endl;
else
{
cout<<"单词查找树中没有这个单词"<<endl;
}
if(tt.SearchTrieTree("liqiang"))
cout<<"在单词查找树中找到了liqiang"<<endl;
else
{
cout<<"单词查找树中没有这个单词"<<endl;
}
if(tt.SearchTrieTree("li"))
cout<<"在单词查找树中找到了li"<<endl;
else
{
cout<<"单词查找树中没有这个单词"<<endl;
}
return 0;
}
测试结果:
----------单词查找树----------
在单词查找树中找到了 爱的宣言
在单词查找树中找到了lichao
单词查找树中没有这个单词lich
在单词查找树中找到了liuyinuo
在单词查找树中找到了upc
单词查找树中没有这个单词
单词查找树中没有这个单词
请按任意键继续. . .
思想:用字符的ascii码值减去基准值转化为索引值