决策树模型: ID3 、C4.5、C5.0、CART、CHAID、Quest比较
一、决策树的核心思想
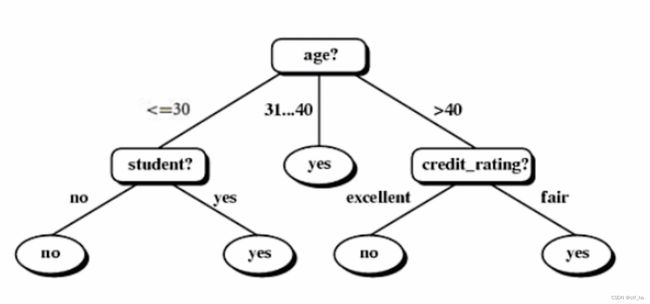
决策树:从根节点开始一步步走到叶子节点(决策),所有的数据最终都会落到叶子节点,既可以做分类也可以做回归。
- 树的组成
- 根节点(root node):第一个选择点,有零条或者多条出边的点;
- 内部点(internal node):只有一条入边并且有两条或多条出边的点;
- 叶节点(leaf node):最终的决策结果;
决策树学习的目的是为了产生一颗泛化能力强,即处理未见示例能力强的决策树,其基本流程遵循简单且直观的“分而治之”(divide-and-conquer).
-
优点
1、可以处理非线性问题
2、可解释强,没有参数
3、模型简单直观,预测效率高 -
缺点
1、不支持在线学习,当新的样本进来,需要重新构建树
2、容易发生过拟合现象
3、学习准确率不如其它模型,集成学习解决
二、决策树的分类与流派
- 如何切分特征(选择节点)
问题:根节点的选择该用哪个特征呢?接下来呢?如何切分呢?
2.1 、ID3(Iterative Dichotomiser 3)
从信息论的知识中我们知道:信息熵越大,从而样本纯度越低。D3 算法的核心思想就是以信息增益来度量特征选择,选择信息增益最大的特征进行分裂I。
- 信息增益 1
“信息熵”(information entropy)是表示随机变量不确定性(说白了就是物体内部的混乱程度)的度量的一种指标。
假定当前样本集合D中第K类所占的比例为 p k p_k pk,则D的信息熵定义为:
E n t ( D ) = − ∑ k = 1 n p k l o g 2 p k Ent(D) = -\sum_{k=1}^np_klog_2p_k Ent(D)=−k=1∑npklog2pk
Ent(D)的值越小,则D的纯度越高。
“信息增益”(information gain)的定义为
g a i n ( D , a ) = E n t ( D ) − ∑ v = 1 v ∣ D v ∣ D E n t ( D v ) gain(D,a) = Ent(D)-\sum_{v=1}^v\frac{|D^v|}{D}Ent(D^v) gain(D,a)=Ent(D)−v=1∑vD∣Dv∣Ent(Dv)
其中a为离散属性,V为a中的取值个数{ a 1 , a 2 , . . . , a V a^1,a^2,...,a^V a1,a2,...,aV}, D v D^v Dv为第v个分支点在属性a上的样本。
一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的“纯度”提升越大。
ID3是一个只能围绕离散型变量进行分类问题建模的决策树模型,即ID3无法处理连续型特征、也无法处理回归问题,如果带入训练数据有连续型变量,则首先需要对其进行离散化处理,也就是连续变量分箱。例如如下个人消费数据,各特征都是离散型变量,能够看出,其中age和income两列就是连续型变量分箱之后的结果,例如age列就是以30、40为界进行连续变量分箱。当然,除了如下表示外,我们还可以将分箱之后的结果直接赋予一个离散的值,如1、2、3等。
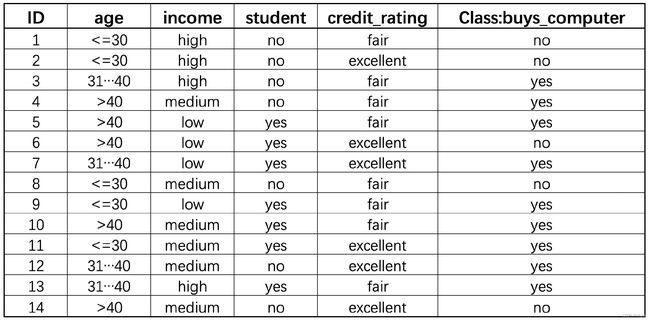
在历史数据中(14个样本中)有9个class为yes,有5个为no,其熵应为:
− 9 14 l o g 2 9 14 − 5 14 l o g 2 5 14 = 0.940 -\frac{9}{14}log_2\frac{9}{14}-\frac{5}{14}log_2\frac{5}{14}=0.940 −149log2149−145log2145=0.940
划分方式:4种,谁当根节点呢?
各属性的信息增益分别为,Gain(age) = 0.247,Gain(income)=0.029、Gain(student)=0.151、Gain(credit_rating)=0.048。很明显,按照age列展开能够更有效的降低数据集的不纯度,因此树的第一层生长就是按照age列的不同取值对数据集进行划分。
接下来需要继续进行迭代,因此该模型最终树的生长形态如下:
此外,需要注意的是,正因为ID3是按照列来进行展开,因此只能处理特征都是离散变量的数据集。另外,根据ID3的建模规则我们不难发现,ID3树在实际生长过程中会更倾向于挑选取值较多的分类变量展开(如有一个特征是“客户ID”,即按此变量划分每个划分都是纯的(即完全的划分,只有属于一个类别),客户ID的信息增益为最大值1。但这种按该自变量的每个值进行分类的方式是没有任何意义的。),但如此一来便更加容易造成模型过拟合,而遗憾的是ID3并没有任何防止过拟合的措施。而这些ID3的缺陷,则正是C4.5算法的改进方向。
2.2 、C4.5
为了避免ID3树在实际生长过程中会更倾向于挑选取值较多的分类变量展开而导致过拟合这个不足,C4.5中是用信息增益比率(gain ratio)来作为选择分支的准则。
- 信息增益比率
信息增益比率通过引入一个被称作分裂信息(Split information)的项来惩罚取值较多的Feature。除此之外,C4.5还弥补了ID3中不能处理特征属性值连续的问题。但是,对连续属性值需要扫描排序,会使C4.5性能下降。这是C4.5的两个重大改进。
“增益率”(gain ratio)定义为:
G a i n _ r a t i o = G a i n ( D , a ) I V ( a ) Gain\_ratio = \frac{Gain(D,a)}{IV(a)} Gain_ratio=IV(a)Gain(D,a)
- 引入分支度Information Value的概念
I V ( a ) = − ∑ v = 1 v ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(a) = -\sum_{v=1}^v\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|} IV(a)=−v=1∑v∣D∣∣Dv∣log2∣D∣∣Dv∣
例如对于上述例子来看:
需要注意的是,增益率则对可取值数目较少的属性有所偏好,因此,C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
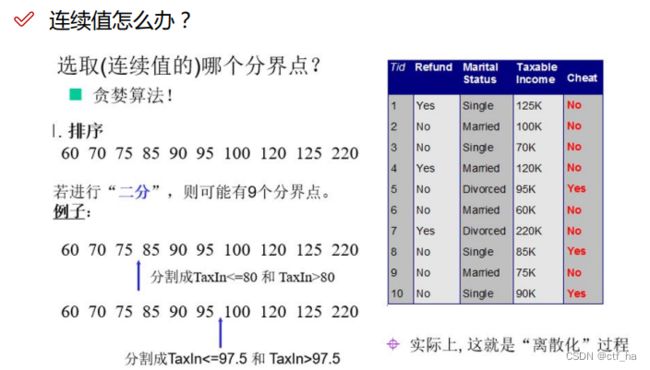
- C4.5的连续变量处理方法
2.3 、C5.0
C5.0是C4.5应用于大数据集上的分类算法,主要在执行效率和内存方面进行了改进,采用Boosting方式提高模型准确率,又称为BoostingTrees,在计算速度比较快,占用的内存资源较少。
由于Clementine的C5.0在很长的一段时间是作为收费软件存在、并且多集成与像SAS软件中,因此并未被最广泛的应用于各领域。
暂不展开
2.4 、CART全称为Classification and Regression Trees,即分类与回归决策树
CART最大的特色它是一棵二叉树,采用二元切分法,每次把数据切成两份,分别进入左子树、右子树。CART决策树使用“基尼指数”(Gini index)来选择划分属性。其定义为:
G i n i ( D ) = ∑ k = 1 V ∑ k ′ ≠ k P k P k ′ = 1 − ∑ k = 1 V p k 2 Gini(D)=\sum_{k=1}^V\sum_{k^{'}≠k}P_kP_{k^{'}}=1-\sum_{k=1}^Vp_k^2 Gini(D)=k=1∑Vk′=k∑PkPk′=1−k=1∑Vpk2
在分类问题中, p k p_k pk表示样本点属于第i类的概率。直观来说,Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率。因此,Gini(D)越小,则数据集D的纯度越高。
如1类样本有6例,0类样本有4例,则
G i n i ( D ) = p ( 1 ) + p ( 0 ) = 1 − ( ( 6 10 ) 2 + ( 4 10 ) 2 ) = 0.48 Gini(D)=p(1)+p(0)=1-((\frac{6}{10})^2+(\frac{4}{10})^2)=0.48 Gini(D)=p(1)+p(0)=1−((106)2+(104)2)=0.48
属性a的基尼指数定义为:
G i n i i n d e x ( D , a ) = ∑ k = 1 V D v D G i n i ( D v ) Gini_index(D,a)=\sum_{k=1}^V\frac{D^v}{D}Gini(D^v) Giniindex(D,a)=k=1∑VDDvGini(Dv)
于是,在候选属性集合A中,选择那个使得划分后基尼指数最小的属性作为划分属性。即 a ∗ = a r g m i n G i n i _ i n d e x ( D , a ) a_*=argmin \ Gini\_index(D,a) a∗=argmin Gini_index(D,a)。
信息熵与Gini指数关系
{ H ( x ) = − ∑ k = 1 k P k l n P k G i n i ( x ) = ∑ k = 1 k P k ( 1 − P k ) = 1 − ∑ k = 1 k P k 2 \left\{ \begin{aligned} H(x)&=-\sum_{k=1}^kP_klnP_k\\ Gini(x)&=\sum_{k=1}^kP_k(1-P_k)\\ &=1-\sum_{k=1}^kP_k^2 \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧H(x)Gini(x)=−k=1∑kPklnPk=k=1∑kPk(1−Pk)=1−k=1∑kPk2
将 f ( x ) = − l n x f(x)=-lnx f(x)=−lnx在x=1处进行一阶泰勒展开:
{ f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + o ( . ) = f ( 1 ) + f ′ ( 1 ) ( x − 1 ) + o ( . ) = 0 − 1. ( x − 1 ) + o ( . ) = 1 − x \left\{ \begin{aligned} f(x)&=f(x_0)+f^{'}(x_0)(x-x_0)+o(.)\\ &=f(1)+f^{'}(1)(x-1)+o(.)\\ &=0-1.(x-1)+o(.)\\ &=1-x \end{aligned} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧f(x)=f(x0)+f′(x0)(x−x0)+o(.)=f(1)+f′(1)(x−1)+o(.)=0−1.(x−1)+o(.)=1−x
因此熵可以近似转化为:
{ H ( x ) = − ∑ k = 1 k P k l n P k = ∑ k = 1 k P k ( − l n P k ) ≈ ∑ k = 1 k P k ( 1 − P k ) = G i n i ( x ) \left\{ \begin{aligned} H(x)&=-\sum_{k=1}^kP_klnP_k\\ &=\sum_{k=1}^kP_k(-lnP_k)\\ &\approx\sum_{k=1}^kP_k(1-P_k)=Gini(x)\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧H(x)=−k=1∑kPklnPk=k=1∑kPk(−lnPk)≈k=1∑kPk(1−Pk)=Gini(x)
因此,基尼指数是信息熵-logP在P=1处一阶泰勒展开的结果。
- CART分类树
-
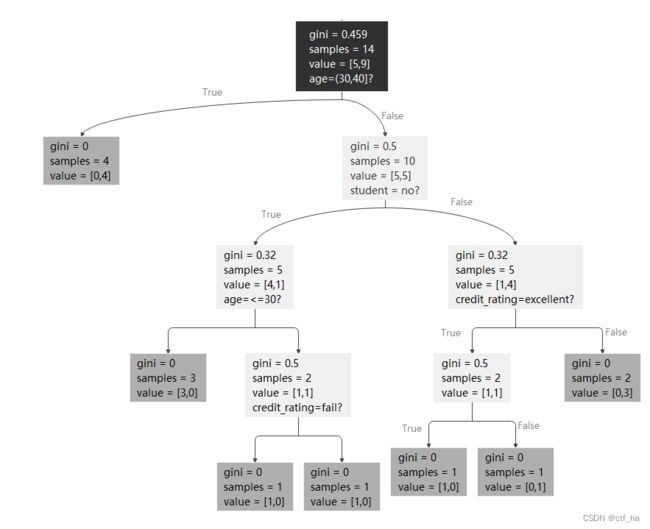
G i n i ( c l a s s ) = 1 − 5 14 2 − 9 14 2 = 0.459 Gini(class) = 1-\frac{5}{14}^2-\frac{9}{14}^2=0.459 Gini(class)=1−1452−1492=0.459
-
G i n i ( D , a g e = < 30 ) = 5 14 ∗ ( 1 − 3 5 2 − 2 5 2 ) = 0.17 Gini(D,age=<30)=\frac{5}{14}*(1-\frac{3}{5}^2-\frac{2}{5}^2)=0.17 Gini(D,age=<30)=145∗(1−532−522)=0.17
-
G i n i ( D , a g e = ( 30 , 40 ] ) = 4 14 ∗ ( 1 − 0 4 2 − 4 4 2 ) = 0 Gini(D,age=(30,40])=\frac{4}{14}*(1-\frac{0}{4}^2-\frac{4}{4}^2)=0 Gini(D,age=(30,40])=144∗(1−402−442)=0
-
G i n i ( D , a g e = > 40 ) = 5 14 ∗ ( 1 − 2 5 2 − 3 5 2 ) = 0.17 Gini(D,age=>40)=\frac{5}{14}*(1-\frac{2}{5}^2-\frac{3}{5}^2)=0.17 Gini(D,age=>40)=145∗(1−522−532)=0.17
接下来需要继续进行迭代,因此该模型最终树的生长形态如下:
- CART回归树
决策树的生成就是递归地构建二叉决策树的过程,对回归树用平方误差最小化准则进行特征选择。
最小二乘回归树生成算法2
输入:训练数据集D;输出:回归树f(x)。
在训练数据集所在的输入空间中,递归地将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树:
- (1)、选择最优切分变量j与切分点s,求解
J = min j . s [ min c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + min c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ] J=\min_{j.s}[\min_{c1}\sum_{x_i \in R_1(j,s)}(y_i-c_1)^2+\min_{c2}\sum_{x_i \in R_2(j,s)}(y_i-c_2)^2] J=j.smin[c1minxi∈R1(j,s)∑(yi−c1)2+c2minxi∈R2(j,s)∑(yi−c2)2]
遍历变量j,对固定的切分变量j扫描切分点s,选择J最小的对(j,s) - (2)、用选定的对(j,s)划分区域并决定相应的输出值:
R 1 ( j , s ) = { x ∣ x j ≤ s } , R 2 ( j , s ) = { x ∣ x j > s } R_1(j,s)=\{x|x^{j}\le s\},R_2(j,s)=\{x|x^{j} > s\} R1(j,s)={x∣xj≤s},R2(j,s)={x∣xj>s}
c ^ m = 1 N m ∑ x i ∈ R m ( j , s ) y i , x ∈ R m , m = 1 , 2 \hat c_m=\frac{1}{N_m}\sum_{x_i\in R_m(j,s)}y_i,x \in R_m,m=1,2 c^m=Nm1xi∈Rm(j,s)∑yi,x∈Rm,m=1,2 - (3)、遍历所有输入变量,找到最优的切分变量j,构成一个对(j, s)。依此将输入空间划分为两个区域。接着,对每个区域重复上述划分过程,直到满足停止条件为止。这样就生成一颗回归树。这样的回归树通常称为最小二乘回归树(least squares regression tree)。
- (4)、将输入空间划分为M个区域 R 1 , R 2 , . . . , R M R_1,R_2,...,R_M R1,R2,...,RM,生成决策树:
f ( x ) = ∑ m = 1 M c ^ m I ( x ∈ R m ) f(x)=\sum_{m=1}^M \hat c_mI(x \in R_m) f(x)=m=1∑Mc^mI(x∈Rm)
回归树示例

根据以上训练数据表,当切分点s=1,此时 R 1 R_1 R1={1}, R 2 R_2 R2={2,3,4,5,6,7,8,9,10},这两个区域的输出值分别为:
c 1 = 4.50 c_1=4.50 c1=4.50
c 2 = 1 9 ( 4.75 + 4.91 + 5.34 + 5.80 + 7.05 + 7.90 + 8.23 + 8.70 + 9.00 ) = 6.85 c_2=\frac{1}{9}(4.75+4.91+5.34+5.80+7.05+7.90+8.23+8.70+9.00)=6.85 c2=91(4.75+4.91+5.34+5.80+7.05+7.90+8.23+8.70+9.00)=6.85
J s = 1 = ( 4.50 − 4.50 ) 2 + ( 4.75 − 6.85 ) 2 + ( 4.91 − 6.85 ) 2 + ( 5.34 − 6.85 ) 2 + ( 5.80 − 6.85 ) 2 + ( 7.05 − 6.85 ) 2 + ( 7.90 − 6.85 ) 2 + ( 8.23 − 6.85 ) 2 + ( 8.70 − 6.85 ) 2 + ( 9.00 − 6.85 ) 2 = 22.65 J_{s=1}=(4.50-4.50)^2+{(4.75-6.85)^2+(4.91-6.85)^2+(5.34-6.85)^2+(5.80-6.85)^2+(7.05-6.85)^2+(7.90-6.85)^2+(8.23-6.85)^2+(8.70-6.85)^2+(9.00-6.85)^2}=22.65 Js=1=(4.50−4.50)2+(4.75−6.85)2+(4.91−6.85)2+(5.34−6.85)2+(5.80−6.85)2+(7.05−6.85)2+(7.90−6.85)2+(8.23−6.85)2+(8.70−6.85)2+(9.00−6.85)2=22.65
同理,当s为其它的切分点时,可以得到下表:
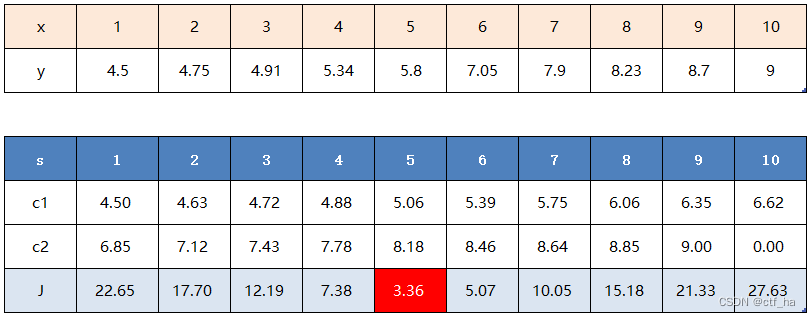
显然取s=5时,J最小。因此,第一个最优切分变量为j=x、最优切分点为s=5。
2.5 、CHAID是Chi-square automatic interaction detection
CHAID是Chi-square automatic interaction detection的简称,由Kass在1975年提出,如果说CART树是一个典型的机器学习算法,那么CHAID树就是一个典型的统计学算法。从该算法的名字就能看出,整个决策树其实是基于卡方检验(Chi-square)的结果来构建的,并且整个决策树的建模流程(树的生长过程)及控制过拟合的方法(剪枝过程)都和C4.5、CART有根本性的区别,例如CART都只能构建二叉树,而CHAID可以构建多分枝的树(注:C4.5也可以构建多分枝的树);例如C4.5和CART的剪枝都是自下而上(Bottom-up)进行剪枝,也被称为修剪法(Pruning Technique),而CHAID树则是自上而下(Top-Down)进行剪枝,也被称为盆栽法(Bonsai Technique)。当然,该决策树算法目前并非主流树模型,因此此处仅作简单介绍,并不做更加深入的探讨。
2.6 、 Quest(Quick Unbiased Efficient Statistical Tree)
它是由Loh和Shih1997年提出的建立决策树的一种二元分类方法,此方法的设计目的是减少大型CART决策树分析所需的处理时间,减少分类树方法中常见的偏向类别较多预测变量的趋势。将分支变量选择和分割点选择以不同的策略进行处理(属性变量为定类,采用卡方检验,定量则采用F检验),选择P值最小且小于显著性水平 α \alpha α的属性变量作为当前的最佳分支变量。运算过程比CART更简单有效。
2.7、总结
| 类型 | ID3 | C4.5 | CART | C5.0 | CHAID | Quest |
|---|---|---|---|---|---|---|
| 支持模型 | 分类 | 分类 | 分类、回归 | 分类 | 分类、回归 | 二值分类 |
| 树结构 | 多叉树 | 多叉树 | 二叉树(特征可以重复使用) | 多叉树 | 多叉树 | 二叉树 |
| 划分标准 | 信息增益 | 信息增益率 | 基尼指数、 平方误差 | 信息增益率 | 卡方检验(Chi-square) | 卡方检验(定类)、F检验(定量) |
| 属性选择 | 选择信息增益最大的属性 | 先找出信息增益高于平均水平的属性,再从中选择增益率最高的 | 选择划分后基尼指数、平方误差最小的属性 | 从统计显著性角度确定分支变量和分割值,进而优化树的分枝过程 | 选择P值最小且小于显著性水平 α \alpha α的属性变量 | |
| 连续型变量 | 不支持 | 二分法 | 二分法 | 二分法 | 支持 | 支持 |
| 缺失值处理 | 不支持(对缺失值敏感) | 支持 | 支持 | 支持 | 支持 | 支持 |
| 剪枝策略 | 无 | PEP悲观剪枝 | CCP基于代价复杂度 | 盆栽法(Bonsai Technique) | ||
| 优缺点 | 会偏向可取值数目加多的属性、算法会生成很深的树,容易产生过拟合现象 | 会偏向可取值数目加少的属性、运算效率低,适用于小数据集。 | 执行效率和内存使用改进、适用大数据集 | 多分类需转换为二分类;运算过程比CRAT更简单、不可以应用权数变量?; |
2.5、其它思考
- 数值型特征分别是怎么处理的?
采用二分法对连续属性进行处理。给定样本集D和连续属性a,假定a在D上出现了n个不同的取值,将这些值从小到大排序,记为 a 1 , a 2 , … , a n {a^1,a^2,…,a^n} a1,a2,…,an。对连续属性a,我们可考察包含n-1个元素的候选划分点集合。
- 在选择分裂属性的时候,训练样本存在缺失值,如何处理?
假如你使用ID3算法,那么选择分类属性时,就要计算所有属性的熵增(信息增益,Gain)。假设10个样本,属性是a,b,c。在计算a属性熵时发现,第10个样本的a属性缺失,那么就把第10个样本去掉,前9个样本组成新的样本集,在新样本集上按正常方法计算a属性的熵增。然后结果乘0.9(新样本占raw样本的比例),就是a属性最终的熵。
- 分类属性选择完成,对训练样本分类,发现属性缺失怎么办?
比如该节点是根据a属性划分,但是待分类样本a属性缺失,怎么办呢?假设a属性离散,有1,2两种取值,那么就把该样本分配到两个子节点中去,但是权重由1变为相应离散值个数占样本的比例。然后计算错误率的时候,注意,不是每个样本都是权重为1,存在分数。
- 训练完成,给测试集样本分类,有缺失值怎么办?
这时候,就不能按比例分配了,因为你必须给该样本一个确定的label,而不是薛定谔的label。这时候根据投票来确定,或者填充缺失值。
- 决策树怎么控制过拟合?
决策树生成算法递归地产生决策树,直到不能继续下去为止。这样产生的树往往对训练数据的分类很准确,但对未知的测试数据的分类却没有那么准确,即过拟合现象。过拟合的原因在于决策树过于复杂,通过剪枝,从已生成的树上裁剪掉一些子树或叶结点,并将其根节点或父节点作为新的叶结点,从而简化树模型,降低过拟合。
- 常用的剪枝方法有预剪枝和后剪枝?
我们还可以通过控制树深,对样本或特征进行采样,控制分裂叶子节点最少样本数,最小gain提升等来控制过拟合
- 决策树/随机森林的特征重要度是怎么获得的?
a.考察样本经过节点后不纯度减少的值的大小,值越大则特征越重要。
b.通过包外数据(out of bag)计算特征加入噪声前后对模型预测准确率的影响,影响越大则特征越重要。
- SVM、LR、决策树的对比?
模型复杂度:SVM 支持核函数,可处理线性非线性问题;LR 模型简单,训练速度快,适合处理线性问题;决策树容易过拟合,需要进行剪枝。
损失函数:SVM hinge loss; LR L2 正则化; Adaboost 指数损失。
数据敏感度:SVM 添加容忍度对 outlier 不敏感,只关心支持向量,且需要先做归一化; LR 对远点敏感。
数据量:数据量大就用 LR,数据量小且特征少就用 SVM 非线性核。
《机器学习》,周志华 ↩︎
《统计学习方法》,李航著,P55-P75; ↩︎