使用PyTorch实现二元分类
导 读
在机器学习领域,二元分类是一项基本任务,是许多实际应用的基石。无论是垃圾邮件检测、情绪分析、医疗诊断还是欺诈检测,二元分类在基于数据的决策中都发挥着关键作用。在本文中,我们将使用PyTorch 实现二分类任务。
二元分类涉及将数据点分类为两个类或类别之一。类似使用过滤器来区分苹果和橙子、积极情绪和消极情绪、或者健康患者和疾病患者。二元分类的强大之处在于它的简单性和对广泛问题的适用性。
本期『数据』已上传百度网盘。
有需要的朋友关注公众号【小Z的科研日常】,回复关键词[二分类]获取。
01、为什么选择Pytorch
PyTorch 因其动态计算图、灵活的架构和强大的生态系统而在深度学习领域中获得了广泛的欢迎。在为各种机器学习任务构建神经网络时,它已成为初学者和资深学者们的首选。
在本文中,我们将探讨 PyTorch 如何简化构建、训练和评估二元分类模型的过程。我们将分解所涉及的关键组件和步骤,使深度学习新手能够轻松上手。
02、加载数据集
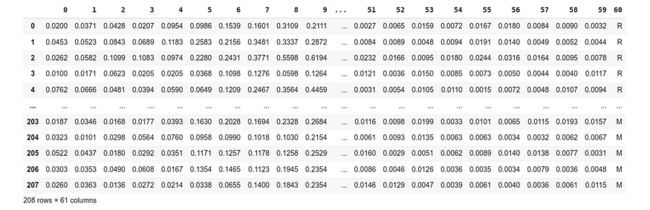
“sonar.all-data”数据集是机器学习领域中的一个经典示例。它源自声纳信号数据,其目标是区分两类:岩石(表示为“R”)和地雷(表示为“M”)。这个二元分类问题是根据声纳信号模式将水下物体识别为地雷或岩石。
以下是有关数据集的信息:
特征数量:数据集中的每个数据点代表一个声纳信号,有 60 个数字特征。这些功能捕获信号的不同方面。
目标标签:数据集具有二进制标签:“R”代表岩石,“M”代表地雷。
!wget https://archive.ics.uci.edu/ml/machine-learning-databases/undocumented/connectionist-bench/sonar/sonar.all-datimport pandas as pd
# 读取数据
data = pd.read_csv("/content/sonar.all-data", header=None)
X = data.iloc[:, 0:60]
y = data.iloc[:, 60]03、目标值标签编码
与许多其他机器学习框架一样,PyTorch 期望目标标签是数值。标签编码是将分类标签映射到整数的过程。
在我们的数据集中,我们将“R”编码为 0,“M”编码为 1。这种编码允许我们的模型计算损失、进行预测并有效学习。
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
encoder.fit(y)
y = encoder.transform(y)04、转换数据为Pytorch张量
经过数据集的加载和预处理,现在是时候为 PyTorch 模型准备数据了。
PyTorch 主要操作张量,即多维数组,在 GPU 上能够高效处理。在本节中,我们将输入特征(X)和目标标签(y)转换为 PyTorch 张量。
import torch
X = torch.tensor(X.values, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.float32).reshape(-1, 1)05、构建二元分类模型
在深度学习领域,神经网络模型是机器学习解决方案的核心和灵魂。对于使用“sonar.all-data”数据集的二元分类任务,我们将使用 PyTorch 创建一个简单的神经网络。这个模型被恰当地命名为 Deep ,将作为我们的二元分类器。
class Deep(nn.Module):
def __init__(self):
super().__init__()
self.layer1 = nn.Linear(60, 60)
self.act1 = nn.ReLU()
self.layer2 = nn.Linear(60, 60)
self.act2 = nn.ReLU()
self.layer3 = nn.Linear(60, 60)
self.act3 = nn.ReLU()
self.output = nn.Linear(60, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.act1(self.layer1(x))
x = self.act2(self.layer2(x))
x = self.act3(self.layer3(x))
x = self.sigmoid(self.output(x))
return x-
三个隐藏层(
layer1、layer2和layer3),每个隐藏层都有 60 个单元和 ReLU 激活函数。 -
具有单个单元的输出层 (
output),表示二元分类决策。 -
应用于输出的 sigmoid 激活函数 (
sigmoid) 将值压缩在 0 和 1 之间。
06、训练模型
首先,定义一个名为model_train的函数,该函数接受模型对象、训练数据集(包括特征和标签)、验证数据集(包括特征和标签)作为输入。
在函数内部,定义损失函数为二元交叉熵(BCELoss),优化器采用Adam优化算法,学习率为0.0001。然后设置训练过程的参数,包括训练的epochs数量(n_epochs)和每个epoch中的batch大小(batch_size)。
接着,在每个epoch的训练过程中,循环遍历数据集,并根据batch大小将数据划分为小批量进行训练。对于每个小批量数据,首先将模型应用于输入特征,得到预测结果。然后计算预测结果与真实标签之间的损失,并进行反向传播计算梯度,最后利用优化器更新模型的参数。
在每个epoch的训练过程中,还计算了模型在验证集上的准确率,并记录下最佳准确率及对应的模型参数。最终,返回训练过程中达到的最佳准确率。
import copy
import numpy as np
import torch.nn as nn
import torch.optim as optim
import tqdm
def model_train(model, X_train, y_train, X_val, y_val):
# 损失函数和优化器
loss_fn = nn.BCELoss() # 二元交叉熵
optimizer = optim.Adam(model.parameters(), lr=0.0001)
n_epochs = 250 # epochs 数量
batch_size = 10 # epochs 大小
batch_start = torch.arange(0, len(X_train), batch_size)
# 最佳模型
best_acc = - np.inf # 初始化为无穷大
best_weights = None
for epoch in range(n_epochs):
# print(epoch)
model.train()
with tqdm.tqdm(batch_start, unit="batch", mininterval=0, disable=True) as bar:
bar.set_description(f"Epoch {epoch}")
for start in bar:
X_batch = X_train[start:start+batch_size]
y_batch = y_train[start:start+batch_size]
# 前馈
y_pred = model(X_batch)
loss = loss_fn(y_pred, y_batch)
# backward pass
optimizer.zero_grad()
loss.backward()
# 更新权重
optimizer.step()
# 打印过程
acc = (y_pred.round() == y_batch).float().mean()
bar.set_postfix(
loss=float(loss),
acc=float(acc)
)
# 模型准确率
model.eval()
y_pred = model(X_val)
acc = (y_pred.round() == y_val).float().mean()
acc = float(acc)
if acc > best_acc:
best_acc = acc
best_weights = copy.deepcopy(model.state_dict())
# 返回最佳精度模型
model.load_state_dict(best_weights)
return best_accfrom sklearn.model_selection import StratifiedKFold, train_test_split
# 训练-测试分割:保留用于最终模型评估的测试集
# 定义 5 折交叉验证测试工具
kfold = StratifiedKFold(n_splits=5, shuffle=True)
cv_scores = []
for train , test in kfold.split(X, y):
# 创建模型,训练并获得准确率
model = Deep()
acc = model_train(model, X[train], y[train], X[ test ], y[ test ])
print ( "准确率: %.2f" % acc)
cv_scores.append(acc)
# 评估模型
acc = np.mean(cv_scores)
std = np.std(cv_scores)
print ( "模型准确率: % .2f%% (+/- %.2f%%)" % (acc*100, std*100))输出结果:
准确度(宽):0.88
准确度(宽):0.86
准确度(宽):0.76
准确度(宽):0.90
准确度(宽):0.88
模型精度:85.61% (+/- 4.92%)