python 基础知识点(蓝桥杯python科目个人复习计划34)
今日复习内容:以做题为主
例题1:Alice 和 Bob的爱恨情仇
题目描述:
Alice和Bob最近正在学习博弈论,为了学以致用,他们找来了一大堆的小饼干 ,并通过博弈的方式来吃掉这些小饼干。他们轮流对这些饼干进行操作,操作规则如下:
由Alice先手,每次从一堆小饼干中拿出k^m个小饼干(k为奇数且m >= 0 ,且k^m不能超过这堆小饼干的总数)。
当一方进行完操作后,如果已经没有剩余的小饼干,则该方获胜,赢得所有的小饼干。
Alice和Bob都想赢得所有的小饼干,所以都会以最佳方式来取小饼干,请问他们之中谁能赢得所有的小饼干?
输入格式:
第一行,输入两个正整数n(1 <= n <= 10^6),k(1 <= k <= 10^9),分别表示饼干的堆数和每次取出饼干的底数。
第二行,输入n个整数,表示第i堆中有ai个小饼干(1 <= ai <= 10^6)。
输出格式:
输出一行,包含一个字符串,输出Alice和Bob之间获胜的那个人。
参考答案:
n,k = map(int,input().split())
li = list(map(int,input().split()))
s = 0 # 用来记录有多少个奇数堆饼干
for i in li:
s += (i%2)
if s % 2:
print('Alice')
else:
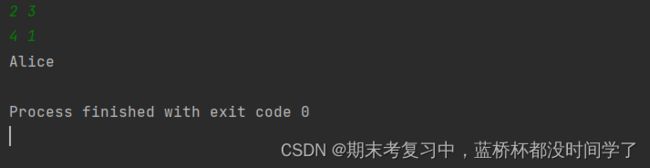
print('Bob')运行结果:
例题2:大石头的搬运工
题目描述:
在一款名为“大石头的搬运工”的游戏中,玩家需要操作一排n堆石头,进行n-1轮游戏。
每一轮,玩家可以选择一堆石头,并将其移动到任意位置。
在n-1轮移动结束时,要求将所有的石头移动到一起(即所有石头的位置相同)即为成功。
移动的费用为石头的重量乘以移动的距离。例如:如果一堆重量为2的石头从位置3移动到位置5,那么费用为2 * (5 - 3) = 4。
请计算出所有合法方案中,将所有石头移动到一起的最小费用。
可能有多堆石头在同一个位置上,但是一轮只能选择移动其中一堆。
输入格式:
第一行一个整数n,表示石头的数量。
接下来n行,每行两个整数Wi和Pi,分别表示第i个石头的重量和初始位置。
输出格式:
输出一个整数,表示最小的总移动费用。
参考答案:
import math
n = int(input())
li = []
for i in range(n):
li.append(list(map(int,input().split())))
li.sort(key = lambda x:x[1])
pex = [0] # 存放第i个石头之前所有石头移动到这里所需要的费用
nex = [0] # 存放第i个石头之后所有石头移动到这里所需要的费用
s = li[0][0] # 存放第i个石头之前所有石头的重量
s1 = li[-1][0] # 存放第i个石头之后所有石头的重量
for i in range(1,n):
pex.append(pex[-1] + s * (li[i][1] - li[i-1][1]))
s += li[i][0]
for i in range(n-2,-1,-1):
nex.append(nex[-1] + s1 * (li[i+1][1] - li[i][1]))
s1 += li[i][0]
nex.reverse()
res = math.inf
for i in range(n):
res = min(res,pex[i] + nex[i])
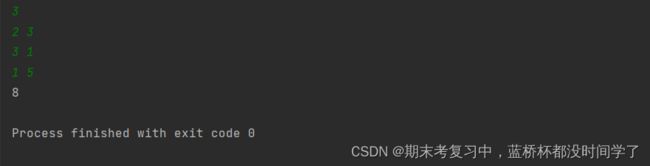
print(res)运行结果:
例题3:最大数组和
题目描述:
小明是一名勇敢的冒险家,他在一次探险途中发现了一组神秘的宝石,这些宝石的价值都不同。但是,他发现这些宝石会随着时间的推移逐渐失去价值,因此他必须在规定的次数内对它们进行处理。
小明想要最大化这些宝石的总价值。他有两种处理方式:
1.选出两个最小的宝石,并将它们从宝石组中删除。
2.选出最大的宝石,并将其从宝石组中删除。
现在,给你小明手上的宝石组,请你告诉他在规定的次数内,最大化宝石的总价值是多少?
输入描述:
第一行包含一个整数t,表示数据组数。
对于每组数据,第一行包含两个整数n和k,表示宝石的数量和规定的处理次数。
第二行包含n个整数,a1,a2,a3,...an,表示每个宝石的价值。
输出描述:
对于每组数据,输出一个整数,表示在规定的次数内,最大化宝石的总价值。
参考答案:
import math
t = int(input())
for kk in range(t):
n,k = map(int,input().split())
li = list(map(int,input().split()))
li.sort()
pex = [0]
for i in range(n):
pex.append(pex[-1] + li[i])
ans = -math.inf
for i in range(k+1):
ans = max(ans,pex[n-(k-i)] - pex[2*i])
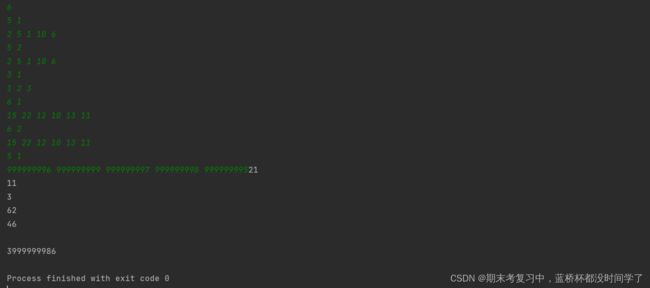
print(ans)运行结果:
例题4:四元组问题
题目描述:
从小学开始,小明就是一个非常喜欢数学的孩子。他喜欢用数学的方式解决各种问题。在他的高中时期,他遇到了一个非常有趣的问题,那就是给定一个长度为n的整数数组nums,判断是否存在四个不同的下标a,b,c,d,使得a < b < c < d,并且nums[d] < nums[c] < nums[a] < nums[b]。
小明非常喜欢这个问题,他决定用数学的方式来解决它。他首先想到了一个非常简单的方法,那就是暴力枚举。他用四个循环来枚举所有可能的下标组合,然后判断是否满足条件。但是这个方法非常耗时,当 n很大时,计算量会非常大。
所以请求你给出一个快速智慧的解决方法。
输入描述:
输入仅两行,第一行包含一个整数n,第二行包含n个整数,其含义如上所示。
输出描述:
输出仅一行,包含一个字符串,YES表示题目存在上面所述的情况,否则输出NO。
参考答案:
import math
n = int(input())
li = list(map(int,input().split()))
a = -math.inf
stack = []
min_r = [math.inf]*n
for i in range(n-2,-1,-1):
min_r[i] = min(min_r[i+1],li[i+1])
flag = False
for i in range(n):
if li[i] < a and li[i] > min_r[i]:
print('YES')
flag = True
break
while stack and li[i] > stack[-1]:
a = max(a,stack[-1])
stack.pop()
stack.append(li[i])
if not flag:
print('NO')运行结果:
这次做的题,对我来说有点难,所以我暂时只做了4题,用了整整一天。
这篇就写到这里,题当然要做,但我得先把知识点复习完。下一篇继续!