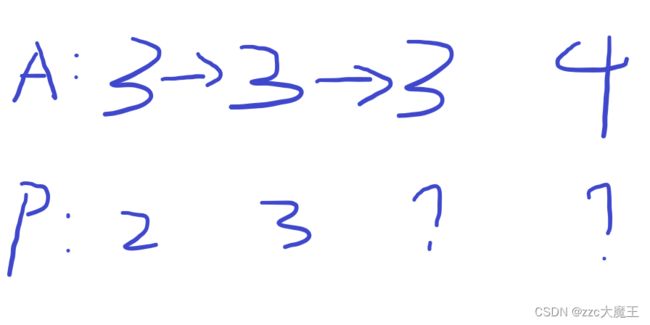AtCoder Regular Contest 171（A~B）

A - No Attacking

N*N棋盘上，放A个rook棋和B个pawn棋。

条件1：假设（i，j）上有一个rook，那么这 i 行和这 j 列，都不能再有其他棋子。

条件2：假设（i，j）上有一个pawn，那么（i-1，j）上不能有棋子。

满足条件的情况下，能放完A个rook和B个pawn，输出Yes，放不完则输出No。

分析：两个条件操作起来太麻烦了，先考虑把其中一个条件解决，条件2约束的只有两个格子，而条件1是一行和一列。所以选择先把棋盘放满pawn棋，假设0为空，1为rook，2为pawn。

接下来再去放rook棋（全部放对角线上方便处理），放在0上，减少了3个pawn；放在2上，则会减少7个pawn。

所以我们需要先把能用的0行放完，没地方放了再放到2上。

#include 
#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define fr first
#define se second
#define endl '\n'
using namespace std;

int n,a,b;
bool flag=false;

void solve(){
    cin>>n>>a>>b;
    int all=(n)*(n/2+n%2),cost=n/2+n%2,tmp=n/2;
    //一共有all个pawn棋（奇数整除之后还少一行，要加上n%2）
    //每次往0行上放一个rook棋会减少cost个pawn棋（奇数会多一个，加n%2）,有tmp个0行
    
//    while(a){//放rook棋
//        a--;
//        if(tmp){//还有0行
//            all-=cost;//每次减少cost个
//            tmp--;
//        }else{
//            cost--;//规律减少,最终能放的内容会变成cost*cost个
//            flag=true;
//        }
//    }
    
    if(a<=tmp){//此处if块由上面while简化得出,上面循环总复杂度a*T有超时的可能性
        all-=cost*a;
    }else{
        flag=true;
        cost-=a-tmp;
    }

    if(flag==false){
        if(all>=b)cout<<"Yes"<=b)cout<<"Yes"<>t;
    while(t--)solve(),init();
    return 0;
}

补题：B - Chmax

序列A：3 3 3 4（输入）

序列P：1 2 3 4（1~N的任意一个排列，也可以是1 2 4 3，4 3 2 1等等）

序列B：1 2 3 4（限定为1~N，若N=5则B：1 2 3 4 5）

操作：找到最小的Bi，若Bi＜P(Bi)，则Bi=P(Bi)。（可以证明成功交换的操作次数是有限的）

在执行完所有成功交换的操作下，问有多少个P序列可以让序列B成为序列A。（B ---P---> A）

分析：模拟一下题目操作，就是类似一个链式前向星的东西，或者说并查集也可以。

1会先变成2，然后变成3，最终变成4（条件限制因只能往大的变，所以最后不会变成1）

所以根据A去逆推P的可能

前面3的肯定是链在一起的（因为是一个排列，不会出现多个3）

所以P的前两个一定是2和3，不然就无解，根据条件第三个可以在1~3之内任选

第四个也可以是1~4里面任选一个。

此处2和3已经被用了，所以第三个只能填1，第四个只能填4

#include 
#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define fr first
#define se second
#define endl '\n'
using namespace std;
const int N=2e5+5,MOD=998244353;

int n,a[N],ans=1,b[N],cnt,use[N];

void noans(){
    cout<<0<>n;
    per(i,1,n)cin>>a[i];

    per(i,1,n)if(a[i]=i或者a[i]==a[a[i]]
    //Bi最小都有Bi=i,B在P的链操作下只能变得更大，不能变小，所以a[i]i时a[i]==a[a[i]]（往后链）】,否则无解。
    
    rep(i,n,1){//逆序循环
        if(!b[a[i]])b[a[i]]=i;//最后出现的下标
        else {
            int tmp=a[i];//要预先保留a[i]的值,不然下面a[i]就变了
            a[i]=b[a[i]];//往前推，如果有出现过的，前面要往后链，则固定一个数。
            b[tmp]=i;
            use[a[i]]=true;
        }
    }

    per(i,1,n){
        if(!use[i])cnt++;//每一位都可以使用1~N中未固定的数（累乘，组合数学）
        if(a[i]==i)ans*=cnt,ans%=MOD,cnt--;//使用之后记得cnt--
        //(ans*=cnt)%=MOD   这样简写是可以的，不要错写成ans*=cnt%=MOD,或者ans*=(cnt)%=MOD
    }

    cout<