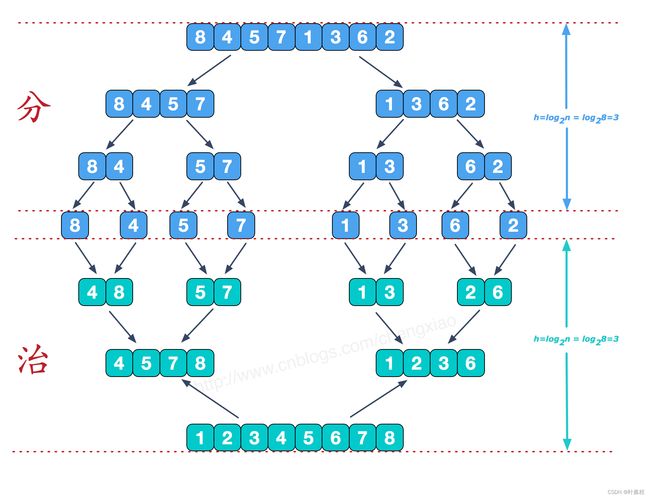
归并排序_MergeSort

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：

• 自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）
• 自下而上的迭代

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间。

2. 算法步骤

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列

2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置

3. 比较两个指针所指向的元素，选择小的元素放入到合并空间，并移动指针到下一位置重复步骤 3 直到某一指针达到序列尾

4. 将另一序列剩下的所有元素直接复制到合并序列尾

3. 动图演示 

4.代码实现

4.1-C语言

4.1.1-递归版

int min(int x, int y) {
    return x < y ? x : y;
}
void merge_sort(int arr[], int len) {
    int *a = arr;
    int *b = (int *) malloc(len * sizeof(int));
    int seg, start;
    for (seg = 1; seg < len; seg += seg) {
        for (start = 0; start < len; start += seg * 2) {
            int low = start, mid = min(start + seg, len), high = min(start + seg * 2, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        int *temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        int i;
        for (i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    free(b);
}

4.1.2-迭代版

void merge_sort_recursive(int arr[], int reg[], int start, int end) {
    if (start >= end)
        return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive(arr, reg, start1, end1);
    merge_sort_recursive(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
        reg[k++] = arr[start1++];
    while (start2 <= end2)
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}

void merge_sort(int arr[], const int len) {
    int reg[len];
    merge_sort_recursive(arr, reg, 0, len - 1);
}

4.2-C++

4.2.1-迭代版

//迭代版本
template
void merge_sort(T arr[], int len) {
    T *a = arr;
    T *b = new T[len];
    for (int seg = 1; seg < len; seg += seg) {
        for (int start = 0; start < len; start += seg + seg) {
            int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        T *temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        for (int i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    delete[] b;
}

 4.2.2-递归版

void Merge(vector &Array, int front, int mid, int end) {
    // preconditions:
    // Array[front...mid] is sorted
    // Array[mid+1 ... end] is sorted
    // Copy Array[front ... mid] to LeftSubArray
    // Copy Array[mid+1 ... end] to RightSubArray
    vector LeftSubArray(Array.begin() + front, Array.begin() + mid + 1);
    vector RightSubArray(Array.begin() + mid + 1, Array.begin() + end + 1);
    int idxLeft = 0, idxRight = 0;
    LeftSubArray.insert(LeftSubArray.end(), numeric_limits::max());
    RightSubArray.insert(RightSubArray.end(), numeric_limits::max());
    // Pick min of LeftSubArray[idxLeft] and RightSubArray[idxRight], and put into Array[i]
    for (int i = front; i <= end; i++) {
        if (LeftSubArray[idxLeft] < RightSubArray[idxRight]) {
            Array[i] = LeftSubArray[idxLeft];
            idxLeft++;
        } else {
            Array[i] = RightSubArray[idxRight];
            idxRight++;
        }
    }
}

void MergeSort(vector &Array, int front, int end) {
    if (front >= end)
        return;
    int mid = (front + end) / 2;
    MergeSort(Array, front, mid);
    MergeSort(Array, mid + 1, end);
    Merge(Array, front, mid, end);
}

4.3-Java 

public class MergeSort implements IArraySort {

    @Override
    public int[] sort(int[] sourceArray) throws Exception {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        if (arr.length < 2) {
            return arr;
        }
        int middle = (int) Math.floor(arr.length / 2);

        int[] left = Arrays.copyOfRange(arr, 0, middle);
        int[] right = Arrays.copyOfRange(arr, middle, arr.length);

        return merge(sort(left), sort(right));
    }

    protected int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        int i = 0;
        while (left.length > 0 && right.length > 0) {
            if (left[0] <= right[0]) {
                result[i++] = left[0];
                left = Arrays.copyOfRange(left, 1, left.length);
            } else {
                result[i++] = right[0];
                right = Arrays.copyOfRange(right, 1, right.length);
            }
        }

        while (left.length > 0) {
            result[i++] = left[0];
            left = Arrays.copyOfRange(left, 1, left.length);
        }

        while (right.length > 0) {
            result[i++] = right[0];
            right = Arrays.copyOfRange(right, 1, right.length);
        }

        return result;
    }

}