二叉树的堂兄弟结点II

1.题目

这道题是2024-2-7的签到题，题目难度为中等。

考察知识点：BFS算法 或 DFS算法。

题目链接：二叉树的堂兄弟结点II

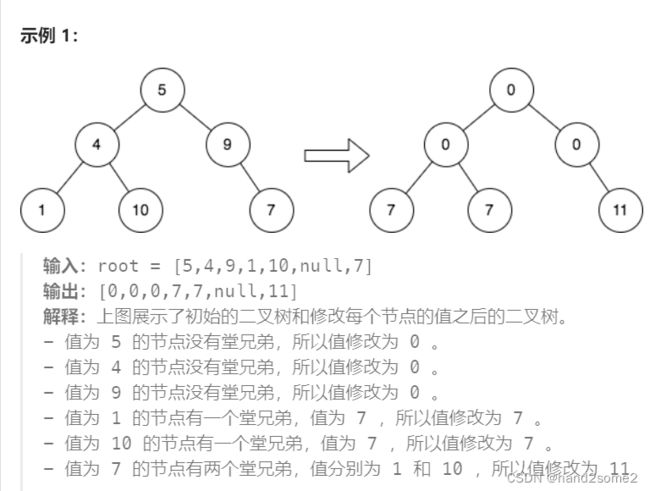
给你一棵二叉树的根 root ，请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。

如果两个节点在树中有相同的深度且它们的父节点不同，那么它们互为 堂兄弟 。

请你返回修改值之后，树的根 root 。

注意，一个节点的深度指的是从树根节点到这个节点经过的边数。

2.思路

其实对于树的题目，大部分考核的知识点都是BFS（广度优先搜索）或者DFS（深度优先搜索）这两种算法。一般来说，能够BFS解决的题目那么DFS也能够解决，这道题也不例外，这道题我用两种方法来解决。

BFS解法

什么是BFS？

        对于BFS算法，又称为广度优先搜索算法。顾名思义，它是以遍历当前结点的所有邻居结点优先。举个栗子：

        小王今年大三了还是个单身狗，于是他决定在操场上偶遇女生，这不，他有了5个心仪的女生并获取到她们的联系方式，但他很纠结不知道追求哪个女生，于是学习了BFS算法的他决定同时追求这5个女生，直到他收到所有女生的回应（同意 或 不同意）。这个就是我对BFS的理解，换句话来说就是广撒网——海王。

对于树结构的广度优先算法，我们可以理解为层序遍历，即一层一层遍历。

解题思路

在这题，我们需要考虑一个难点，如何确定其它所有堂兄弟的值呢？这里我们引入一个定义：亲兄弟和堂兄弟。这样我们就好理解了：父母结点一样的兄弟和父母结点不一样的兄弟。那么对于同一层（我们可以理解为同一个辈分）,我们可以得到以下结论：

sum(V(亲兄弟)) + sum(V(堂兄弟)) = sum(V(一层))

sum(V(亲兄弟)) = sum(V(一层)) -   sum(V(堂兄弟))

同时根据题意，我们只需要替换当前结点的值为其它堂兄弟的值，那么我们还可以得到这个结论：

亲兄弟结点被替换的值相等（都是堂兄弟的值）。

那么我们可以先用bfs算法遍历处于同一层的所有结点，将这一层的所有值的和求出来，这样我们就求出来了sum(V(一层))。接着，我们再一次遍历用于求当前结点的亲兄弟的和sum2，即sum(V(亲兄弟))，然后用前面求到的sum(V(一层))减去刚才求得sum2就是要替换的值。

DFS解法

什么是DFS？

对于DFS算法，它又称为深度优先算法。我觉得有BFS身影的地方肯定有DFS算法。他俩都是搜索算法，只是执行的方式不同，它通常也是应用与树结构或者图结构类型的题目。对于树结构，它也有三个专属的名称（前序遍历、中序遍历、后序遍历）。即一直往下搜索，直到不能遍历位置。举个栗子：

        还是小王，他前面追求的5个女生发现他同时追求5个女生的事情后骂他渣男（具体例子看BFS介绍），于是小王决定深情一把，他又找到了5个女生的联系方式，这次他决定不撞南墙不回头，他刚开始只追求1号女生，直到1号女生给出回应（同意 或 不同意），得到1号女生回应后他才开始追求2号女生，以此类推。这个是我对DFS的理解，换句话来说就是深情男子。

3.代码

BFS解法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # 定义一个列表，用于后续BFS遍历
        q = [root]
        # 根节点没有兄弟，因此直接替换为0
        root.val = 0 

        # bfs遍历
        while len(q) > 0:
            # 定义一个临时列表，用于保存下一层的所有结点
            q2 = []
            # 求下一层所有结点的和
            s = 0
            # 遍历当前层的所有结点
            for nd in q:
                # 如果当前结点有左子结点，则加入到q2中，并加入到s里面
                if nd.left:
                    q2.append(nd.left)
                    s += nd.left.val
                # 如果当前结点有右子结点，则加入到q2中，并加入到s里面
                if nd.right:
                    q2.append(nd.right)
                    s += nd.right.val

            # 再次遍历当前层的所有结点
            for nd2 in q:
                # 求当前结点的下一层亲兄弟结点之和
                sum2 = (nd2.left.val if nd2.left else 0) + (nd2.right.val if nd2.right else 0)
                # 如果当前结点有左子结点
                if nd2.left:
                    nd2.left.val = s - sum2
                # 如果当前结点有右子结点
                if nd2.right:
                    nd2.right.val = s - sum2
            # 更新列表为下一层的结点列表
            q = q2
        return root

DFS解法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # 定义Counter对象，用于求每一层的和
        counts = Counter()
        # 更新根结点
        root.val = 0

        # 第1次dfs遍历（前序遍历）
        def dfs1(node,c):
            # 如果当前结点不为空
            if node:
                # 如果当前结点有左子结点
                if node.left:
                    # 下一层的和加上值
                    counts[c+1] += node.left.val
                # 如果当前结点有右子结点
                if node.right:
                    # 下一层的和加上值
                    counts[c+1] += node.right.val
                # dfs遍历左结点
                dfs1(node.left,c+1)
                # dfs遍历右结点
                dfs1(node.right,c+1)
        
        # 第2次dfs遍历 （前序遍历）
        def dfs2(node,c):
            # 如果当前结点不为空
            if node:
                #求当前结点的孩子结点之和
                s = (node.left.val if node.left else 0) + (node.right.val if node.right else 0)
                # 如果有左子结点
                if node.left:
                    node.left.val = counts[c+1] - s 
                # 如果有右子结点
                if node.right:
                    node.right.val = counts[c+1] - s
                # dfs遍历左结点
                dfs2(node.left,c+1)
                # dfs遍历右结点
                dfs2(node.right,c+1)
        dfs1(root,0)
        dfs2(root,0)
        return root