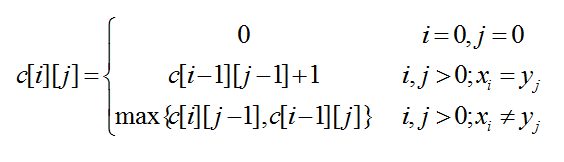动态规划-最长公共子序列问题（LCS）

若给定序列X={x1,x2,…,xm}，则另一序列Z={z1,z2,…,zk} 是X的子序列 是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有：zj=xij。

例如，序列Z={B，C，D，B}是序列X={A，B，C，B，D，A，B}的子序列，相应的递增下标序列为{2，3，5，7}。

给定2个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。

例如，序列X={A，B，C，B，D，A，B}，Y={B，D，C，A，B，A}的子序列，{B，C，A}是X与Y的公共子序列，但不是最长公共子序列；{B，C，B，A}也是X与Y的公共子序列，但它是X与Y的最长公共子序列，因为X与Y没有长度大于4的公共子序列。

给定2个序列X={x1,x2,…,xm}和 Y={y1,y2,…,yn}，找出X和Y的最长公共子序列。

输入：序列X的长度m，序列Y的长度n；序列X各个元素，序列Y各个元素

输出：X与Y的最长公共子序列，最长公共子序列的长度。

运行结果:

解法一：穷举法，列举出X所有可能的子序列，并检查它是否也是Y的子序列，从而确定它是否为公共子序列，在此过程中记录最长的公共子序列

算法复杂度分析： 2从X中任意取l个元素构成子序列，共有2m种不同子集。     

解法二：尝试用动态规划求解

一、 最长公共子序列结构

设序列X = {x1,x2,...xm}和Y= {y1,y2,...yn}的最长公共子序列为Z = {z1,z2,...zk} 则

（1）若Xm = Yn,Zk = Xm = Yn，且Zk-1是Xm-1和Yn-1的最长公共子序列。

（2）若Xm！=Yn且Zk ！= Xm，则Z是Xm-1和Y的最长公共子序列。（反证法：Z是Xm-1和Y的公共子序列，但不是最长的）

（3）若Xm！=Yn且Zk ！=Yn，则Z是X和Yn-1的最长公共子序列。

2个序列的最长公共子序列包含了它们前缀的最长公共子序列。

最长公共子序列问题有最优子结构性质。

二、子问题的递归结构

由最优子结构性质建立子问题最优值的递归关系

用c[i][j]记录序列X和Y的最长公共子序列的长度，其中， Xi={x1,x2,…,xi}；Yj={y1,y2,…,yj}。

当i=0或j=0时，空序列是Xi和Yj的最长公共子序列。故C[i][j]=0。

其他情况下，由最优子结构性质可建立递归关系如下。

三、计算最优值

直接利用递归式的算法是指数时间的，由于在所考虑的子问题空间中，总共有θ(mn)（θ是上下界符号）个不同的子问题，因此，用动态规划算法自底向上地计算最优值能提高算法的效率。
b[i][j]记录c[i][j]是由哪个子问题得到的

void LCSLength(int m, int n, char *x, char *y, int c[][maxn], int b[][maxn])
{
    int i, j;

    c[0][0] = 0;
    for(i = 1; i <= m; i++)
        c[i][0] = 0;
    for(j = 1; j <= n; j++)
        c[0][j] = 0;
    for(i = 1; i <= m; i++)
        for(j = 1; j <= n; j++)
        {
            if(x[i]== y[j])
            {
                c[i][j] = c[i-1][j-1] + 1;
                b[i][j] = 1;
            }
            else if(c[i-1][j] >= c[i][j-1])
            {
                c[i][j] = c[i-1][j];
                b[i][j] = 2;
            }
            else
            {
                c[i][j] = c[i][j-1];
                b[i][j] = 3;
            }
        }
}

四、构造最长公共子序列

LCSLength只是计算出最优值，并未给出最优解，然而数组b可用于快速构造两个序列的最长公共子序列：

b[i][j]=1时表示Xi和Yj的最长公共子序列是由Xi-1和Yj-1的最长公共子序列加上xi所得到(斜) ；

b[i][j]=2时表示Xi和Yj的最长公共子序列与Xi-1和Yj的最长公共子序列相同（上） ；

b[i][j]=3时表示Xi和Yj的最长公共子序列与Xi和Yj-1的最长公共子序列相同（左） 。

根据b的内容打印出最长公共子序列

void LCS(int i, int j, char *x, int b[][maxn])
{
    if(i == 0 || j == 0)
        return;
    if(b[i][j] == 1)
    {
        LCS(i-1, j-1, x, b);
        printf("%c ", x[i]);
    }
    else if(b[i][j] == 2)
        LCS(i-1, j, x, b);
    else
        LCS(i, j-1, x, b);
}