《动手学深度学习(PyTorch版)》笔记8.5

注：书中对代码的讲解并不详细，本文对很多细节做了详细注释。另外，书上的源代码是在Jupyter Notebook上运行的，较为分散，本文将代码集中起来，并加以完善，全部用vscode在python 3.9.18下测试通过，同时对于书上部分章节也做了整合。

Chapter8 Recurrent Neural Networks

8.5 Implementation of RNN from Scratch

8.5.1 Model Defining

import math
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
import matplotlib.pyplot as plt

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

#每个词元都表示为一个数字索引，但将这些索引直接输入神经网络可能会使学习变得困难。
#最简单的表示称为独热编码（one-hot encoding），即将每个索引映射为相互不同的单位向量：
#假设词表中不同词元的数目为N（即len(vocab)），词元索引的范围为0到N-1。
#如果词元的索引是整数i，那么我们将创建一个长度为N的全0向量，并将第i处的元素设置为1。
F.one_hot(torch.tensor([0, 2]), len(vocab))#索引为0和2的独热向量

X = torch.arange(10).reshape((2, 5))
print(F.one_hot(X.T, 28).shape)#形状为（时间步数，批量大小，词表大小）

def get_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device) * 0.01

    # 隐藏层参数
    W_xh = normal((num_inputs, num_hiddens))
    W_hh = normal((num_hiddens, num_hiddens))
    b_h = torch.zeros(num_hiddens, device=device)
    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

def init_rnn_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device), )

def rnn(inputs, state, params):
    # inputs的形状：(时间步数量，批量大小，词表大小)
    W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    # X的形状：(批量大小，词表大小)
    for X in inputs:
        H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)
        Y = torch.mm(H, W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

class RNNModelScratch: #@save
    """从零开始实现的循环神经网络模型"""
    def __init__(self, vocab_size, num_hiddens, device,
                get_params, init_state, forward_fn):
        self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
        self.params = get_params(vocab_size, num_hiddens, device)
        self.init_state, self.forward_fn = init_state, forward_fn

    def __call__(self, X, state):
        X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
        return self.forward_fn(X, state, self.params)

    def begin_state(self, batch_size, device):
        return self.init_state(batch_size, self.num_hiddens, device)
    
num_hiddens = 512
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
                    init_rnn_state, rnn)
state = net.begin_state(X.shape[0], d2l.try_gpu())
Y, new_state = net(X.to(d2l.try_gpu()), state)
print(Y.shape, len(new_state), new_state[0].shape)#隐状态形状不变，仍为(批量大小，隐藏单元数)

def predict_ch8(prefix, num_preds, net, vocab, device):  #@save
    """在prefix后面生成新字符"""
    state = net.begin_state(batch_size=1, device=device)
    outputs = [vocab[prefix[0]]]
    get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
    #get_input()将outputs列表中的最后一个字符的整数标识输入网络
    for y in prefix[1:]:  # 预热期
        _, state = net(get_input(), state)
        outputs.append(vocab[y])
    for _ in range(num_preds):  # 预测num_preds步
        y, state = net(get_input(), state)
        outputs.append(int(y.argmax(dim=1).reshape(1)))
    return ''.join([vocab.idx_to_token[i] for i in outputs])

predict_ch8('time traveller ', 10, net, vocab, d2l.try_gpu())#由于还没有训练网络，会生成荒谬的预测结果

8.5.2 Gradient Clipping

对于长度为$T$的序列，在迭代中计算这$T$个时间步上的梯度，将会在反向传播过程中产生长度为$\mathcal{O}(T)$的矩阵乘法链。当$T$较大时，它可能导致数值不稳定，例如可能导致梯度爆炸或梯度消失。假定在向量形式的$\mathbf{x}$中，或者在小批量数据的负梯度$\mathbf{g}$方向上，使用$\eta >0$作为学习率时，在一次迭代中，我们将$\mathbf{x}$更新为$\mathbf{x}-\eta \mathbf{g}$。如果我们进一步假设目标函数$f$表现良好，即函数$f$在常数$L$下利普希茨连续（Lipschitz continuous），也就是说，对于任意$\mathbf{x}$和$\mathbf{y}$我们有：

$$|f(\mathbf{x})-f(\mathbf{y})|\le L\Vert \mathbf{x}-\mathbf{y}\Vert .$$

在这种情况下，我们可以安全地假设：如果我们通过$\eta \mathbf{g}$更新参数向量，则

$$|f(\mathbf{x})-f(\mathbf{x}-\eta \mathbf{g})|\le L\eta \Vert \mathbf{g}\Vert ,$$

这意味着变化不会超过$L\eta \Vert \mathbf{g}\Vert$的，坏的方面是限制了取得进展的速度；好的方面是限制了事情变糟的程度。有时梯度可能很大，使得优化算法可能无法收敛，我们可以通过降低$\eta$的学习率来解决这个问题。但是如果很少得到大的梯度，一个替代方案是通过将梯度$\mathbf{g}$投影回给定半径（例如$\theta$）的球来截断梯度$\mathbf{g}$，如下式：

$$\mathbf{g}\leftarrow \min \left(1,\frac{\theta }{\Vert \mathbf{g}\Vert }\right)\mathbf{g}.$$

上式使得梯度范数永远不会超过$\theta$，并且更新后的梯度完全与$\mathbf{g}$的原始方向对齐。它还有一个作用，即限制任何给定的小批量数据（以及其中任何给定的样本）对参数向量的影响，这赋予了模型一定程度的稳定性。

def grad_clipping(net, theta):  #@save
    """截断梯度"""
    if isinstance(net, nn.Module):
        params = [p for p in net.parameters() if p.requires_grad]
    else:
        params = net.params
    norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
    if norm > theta:
        for param in params:
            param.grad[:] *= theta / norm

8.5.3 Training

下面训练模型的方式与3.6有三个不同之处：

1. 序列数据的不同采样方法（随机采样和顺序分区）将导致隐状态初始化的差异。
   使用顺序分区时，只在每个迭代周期的开始位置初始化隐状态，由于下一个小批量数据中的第$i$个子序列样本与当前第$i$个子序列样本相邻，因此当前小批量数据最后一个样本的隐状态将用于初始化下一个小批量数据第一个样本的隐状态。这样，存储在隐状态中的序列的历史信息可以在一个迭代周期内流经相邻的子序列，然而在任何一点隐状态的计算，都依赖于同一迭代周期中前面所有的小批量数据，这使得梯度计算变得复杂。为了降低计算量，在处理任何一个小批量数据之前，我们先分离梯度，使得隐状态的梯度计算总是限制在一个小批量数据的时间步内。当使用随机抽样时，需要为每个迭代周期重新初始化隐状态因为每个样本都是在一个随机位置抽样的。
2. 在更新模型参数之前截断梯度，目的是使得即使训练过程中某个点上发生了梯度爆炸，也能保证模型收敛。
3. 用困惑度来评价模型，确保了不同长度的序列具有可比性。

代码如下：

def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter):#@save
    """训练网络一个迭代周期"""
    state, timer = None, d2l.Timer()
    metric = d2l.Accumulator(2)  # 训练损失之和,词元数量
    for X, Y in train_iter:
        if state is None or use_random_iter:
            # 在第一次迭代或使用随机抽样时初始化state
            state = net.begin_state(batch_size=X.shape[0], device=device)
        else:
            if isinstance(net, nn.Module) and not isinstance(state, tuple):
                # state对于nn.GRU是个张量
                state.detach_()
            else:
                # state对于nn.LSTM或对于我们从零开始实现的模型是个张量
                for s in state:
                    s.detach_()
        y = Y.T.reshape(-1)
        X, y = X.to(device), y.to(device)
        y_hat, state = net(X, state)
        l = loss(y_hat, y.long()).mean()
        if isinstance(updater, torch.optim.Optimizer):
            updater.zero_grad()
            l.backward()
            grad_clipping(net, 1)
            updater.step()
        else:
            l.backward()
            grad_clipping(net, 1)
            # 因为已经调用了mean函数
            updater(batch_size=1)
        metric.add(l * y.numel(), y.numel())#y.numel()返回y中元素的数量
    return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()

def train_ch8(net, train_iter, vocab, lr, num_epochs, device,use_random_iter=False):#@save
    """训练模型"""
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
                            legend=['train'], xlim=[10, num_epochs])
    # 初始化
    if isinstance(net, nn.Module):
        updater = torch.optim.SGD(net.parameters(), lr)
    else:
        updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size)
    predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device)
    # 训练和预测
    for epoch in range(num_epochs):
        ppl, speed = train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter)
        if (epoch + 1) % 10 == 0:
            print(predict('time traveller'))
            animator.add(epoch + 1, [ppl])
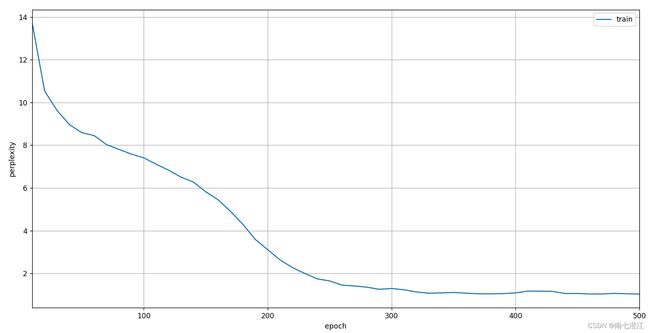
    print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
    print(predict('time traveller'))
    print(predict('traveller'))
    
num_epochs, lr = 500, 1

#使用顺序分区
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu())
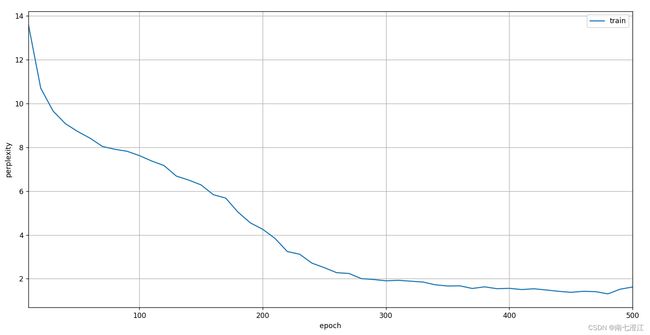
#使用随机抽样
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,init_rnn_state, rnn)
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu(),use_random_iter=True)
plt.show()

顺序分区训练结果:

随机抽样训练结果: