计算机科学与导论 第一章绪论和第二章数字系统
文章预览:
- 1. 计算机软硬件常识(第一章)
-
- 1. 冯诺依曼
- 2. 计算机历史
- 3. 计算机的诞生
- 2. 数字系统(第二章)
-
- 1. 位置化的数字系统
-
-
- 1. 十进制系统
- 2. 二进制系统
- 3. 八进制系统
- 4. 十六进制系统
-
- 2. 转换
-
-
- 1. 其他进制转换到十进制的转换
- 2. 十进制到其他进制的转换
- 3. 数码的数量
- 4. 二进制——十六进制转换
- 5. 二进制——八进制转换
- 6. 八进制—十六进制转换
-
- 3. 数码的问题
1. 计算机软硬件常识(第一章)
1. 冯诺依曼
图灵在1937年首次提出了一个通用计算机设备的设想,他设想所有的计算都能在一中特殊的机器上执行,这就是所说的图灵机
冯诺依曼模型:基于图灵机建造的计算机都在存储中储存数据,冯诺依曼指出,鉴于程序和数据在逻辑上时相同的,因此程序也能存储在计算机存储器中。
4个子系统:基于冯诺依曼模型建造的计算机分为4个子系统:存储器,算术逻辑单元,控制逻辑单元,输入输出单元
算术逻辑单元(ALU)是用来进行计算和逻辑运算的地方。
控制单元式对存储器,算术逻辑单元,输入、输出等子系统进行控制操作的单元
输入子系统负责从计算机外部接受输入数据和程序
输出子系统负责将计算机的处理结果输出到外部
冯诺依曼模型要求程序必须存储在内存当中。
2. 计算机历史
机械计算机器(1930年以前)
电子计算机的诞生(1930~1950)
第一台通用的,完全电子计算机由约翰·莫克利 (John Mauchly)和约瑟夫·雷伯恩 (J. Presper Eckert)发明,这台计算机被称为ENIAC 他是1946年完成设计的,曾有误传ENIAC是第一台计算机,实际上,真正的第一台电子计算机是阿塔纳索夫-贝瑞计算机(Atanasoff–Berry Computer,简称ABC计算机)。事实上ABC计算机不可编程,且非图灵完全,只能进行线性方程组的计算。它的价值是确定了一些现代计算机设计思想,如采用二进制、可重用的存储器等。所以说ENIAC是第一台通用计算机。
第一台冯氏思想的计算机于1950年在宾夕法西亚大学诞生,命名为EDVAC
3. 计算机的诞生
第一代计算机 体积庞大 以电子管(真空管)为电子开关。
第二代计算机使用晶体管代替电子管
第三代计算机(1965~1975)中小规模集成电路(晶体管,导线以及其他部件做在一块单芯片上)的发明更加减少了计算机的成本和大小
第四代计算机出现了微型计算机,第一桌面计算器出现在1975年,电子工业的发展允许计算机系统做在单块电路板上。这一时代还出现了计算机网络
第五代计算机
这个还未终止的时代始于1985年,这个时代见证了掌上计算机和台式计算机的诞生,多媒体的应用和虚拟现实现象。
2. 数字系统(第二章)
1. 位置化的数字系统
在位置化的数字系统中,数字符号所占据的位置决定了其表示的值。在该系统中数字这样表示:
± ( S k − 1 S k − 2 . . . S 2 S 1 S 0 . S − 1 S − 2 . . S − k ) b \pm (S_{k-1}S_{k-2}...S_2S_1S_0.S_{-1}S_{-2}..S_{-k})_b ±(Sk−1Sk−2...S2S1S0.S−1S−2..S−k)b
它的值是 n = ± S k − 1 ∗ b k − 1 + S k − 2 ∗ b k − 2 . . . + S 2 ∗ b 2 + S 1 ∗ b 1 + S 0 ∗ b 0 . S − 1 ∗ b − 1 + S − 2 ∗ b − 2 + . . . S − k ∗ b − k n=\pm S_{k-1}*b^{k-1}+S_{k-2}*b^{k-2}...+S_2*b^2+S_1*b^1+S_0*b^0.S_{-1}*b^{-1}+S_{-2}*b^{-2}+...S_{-k}*b^{-k} n=±Sk−1∗bk−1+Sk−2∗bk−2...+S2∗b2+S1∗b1+S0∗b0.S−1∗b−1+S−2∗b−2+...S−k∗b−k
其中S是一套符号集,b是为底(或基础),他等于S符号集中的符号总数,b的非负数幂与数字的整数部分有关,而负数幂与该数字的小数部分有关, ± \pm ±符号表示该数字可正可负。
1. 十进制系统
b=10,S={0,1,2,3,4,5,6,7,8,9} 用数码k表示十进制的最大值为 N = 1 0 K − 1 N=10^K-1 N=10K−1
2. 二进制系统
b=2,S={0,1} 用数码k表示二进制的最大值为 N = 2 K − 1 N=2^K-1 N=2K−1
3. 八进制系统
b=8,S={0,1,2,3,4,5,6,7} 用数码k表示八进制的最大值为 N = 8 K − 1 N=8^K-1 N=8K−1
4. 十六进制系统
b=16,S={0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} 用数码k表示十六进制的最大值为 N = 1 6 K − 1 N=16^K-1 N=16K−1
2. 转换
1. 其他进制转换到十进制的转换
这种转换简单而迅速,说白了就是按权展开求和得到十进制数。
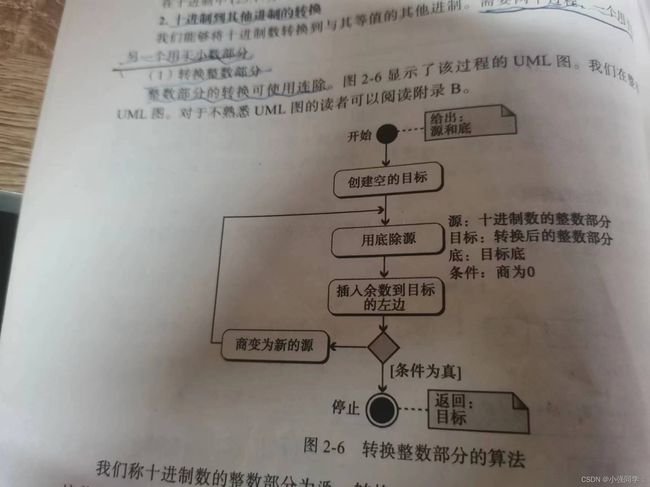
2. 十进制到其他进制的转换
我们将十进制转换到其等值的其他进制,需要俩个过程,一个用于整数部分,另一个用于小数部分。‘
整数部分的转换用连除,下面使用了UML图
’
转换小数部分
小数部分可使用连乘法,取整数。
3. 数码的数量
说白了就是几位数,我们看看把一个十进制整数换算为其他常用进制会变成多少位。
我们推一下 想想原理 设十进制整数为N 那我们要的为其他进制下为x位刚好能表示这个数那么肯定有 b x − 1 < = N < = b x − 1 b^{x-1}<=N<=b^{x}-1 bx−1<=N<=bx−1 俩边同时取对数 可得出不等式 x < = l o g b N + 1 x<=log_b^N+1 x<=logbN+1 x必定是整数,所以
x = ⌊ l o g b N ⌋ + 1 x=⌊ log_b^N⌋+1 x=⌊logbN⌋+1 书上写的公式不对,不是上限而应该是下限+1,举例整数2换成2进制为10,那是为2位,如果按书上公式因为1.很明显不对。
4. 二进制——十六进制转换
我们能将数字从二进制转换到十六进制,反之亦然,这是因为在这俩个底之间存在关系,二进制的4位刚好是十六进制的1位,4个二进制转换成一个16进制数即可,不足补零。
5. 二进制——八进制转换
和十六进制与二进制转换很像,只不过要变成3个二进制换成一个八进制数,反之亦然,不足补零
6. 八进制—十六进制转换
这有俩种办法,一种是通过十进制为中介,另一种是通过二进制为中介。
3. 数码的问题
前面我们小试牛刀,试过把一个整数N换成其他进制数要几位,现在我们更深层次想一下,如果我们知道源系统数码的最大数量,就能知道我们在目标系统中所需要的最小数量。例如在源系统中我们知道使用6个十进制数码,那么在目标系统中我们就知道要使用二进制数码的最少数量。通常假设在 b 1 b_1 b1为底的系统中使用了k个数码,在源系统中显示的最大数为 b 1 k − 1 b_1^k-1 b1k−1,
假设我们在目标系统中需要x位数码(也就是我们要求的),底为 b 2 b_2 b2这个条件已知。那么有不等式为 b 2 x − 1 > = b 1 k − 1 b_2^x-1>=b_1^k-1 b2x−1>=b1k−1
利用同时取对数并利用换底公式 能得到不等式为 x > = k ∗ l o g b 2 b 1 x>=k*log_{b2}^{b1} x>=k∗logb2b1 即 x = ⌈ k ∗ l o g b 2 b 1 ⌉ = ⌈ k ∗ l o g 10 b 1 / l o g 10 b 2 ⌉ x=⌈k*log_{b2}^{b1}⌉=⌈k*log_{10}^{b1}/log_{10}^{b2}⌉ x=⌈k∗logb2b1⌉=⌈k∗log10b1/log10b2⌉
公式例子:
找出2进制数码的最小数,用于存储一个最大6个数码的十进制数整数。
k=6, b 1 b_1 b1=10 , b 2 = 2 b_2=2 b2=2 求x
带入公式:
x = ⌈ 6 ∗ l o g 2 10 ⌉ = ⌈ 6 ∗ l o g 10 10 / l o g 10 2 ⌉ = 20 x=⌈6*log_{2}^{10}⌉=⌈6*log_{10}^{10}/log_{10}^{2}⌉=20 x=⌈6∗log210⌉=⌈6∗log1010/log102⌉=20
储存一个最大6个数码的十进制整数需要2进制数码20位才可以。
