机器学习入门--逻辑回归与简单二分类数据实战

逻辑回归

在机器学习领域，逻辑回归是一个广泛应用于分类问题的算法。与线性回归不同，逻辑回归用于预测离散的类别标签，可以处理二分类和多分类问题。下面我们将介绍逻辑回归的基本原理和实现方式。

原理

逻辑回归的目标是找到一个函数 $g(z)$，将输入的特征向量 $x$ 映射到概率值 $p(y=1|x;w)$，其中 $w$ 是参数向量。我们可以使用 sigmoid 函数来实现这个映射：

$$g(z)=\frac{1}{1+e^{-z}}$$

其中 $z=w^{T}x$ 是输入特征向量 $x$ 和参数向量 $w$ 的内积。sigmoid 函数的图像如下所示：

我们可以将 $g(z)$ 的输出解释为 $y=1$ 的概率，因此 $1-g(z)$ 可以解释为 $y=0$ 的概率。根据贝叶斯定理，我们可以将 $p(y=1|x;w)$ 表示为：

$$p(y=1|x;w)=\frac{p(x|y=1)p(y=1)}{p(x|y=1)p(y=1)+p(x|y=0)p(y=0)}$$

其中 $p(x|y=1)$ 和 $p(x|y=0)$ 是输入特征向量 $x$ 在类别 $y=1$ 和 $y=0$ 下的概率分布，$p(y=1)$ 和 $p(y=0)$ 是类别 $y=1$ 和 $y=0$ 的先验概率。通过对上式进行变形和简化，我们可以得到：

$$p(y=1|x;w)=\frac{1}{1+e^{-w^{T}x}}$$

这个式子就是逻辑回归模型的基本形式。我们可以使用最大似然估计来求解参数向量 $w$。

代码实现

在实现逻辑回归之前，我们需要准备数据集，并进行数据预处理和特征工程。这里我们使用 scikit-learn 提供的 iris 数据集进行演示。我们只选择前两个特征，并对类别进行二分类。

# By Dr.Cup
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

# 加载数据集
iris = load_iris()

# 提取前两个特征和对应的目标值
X = iris.data[:, :2]
y = iris.target

# 仅保留类别为0和1的样本
X = X[y < 2]
y = y[y < 2]

# 特征缩放
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建逻辑回归模型
model = LogisticRegression()

# 在训练集上训练模型
model.fit(X_train, y_train)

# 生成网格点坐标
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

# 对网格点进行预测
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 绘制分类结果的图像
plt.figure()
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='red')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('Iris Binary Classification - Logistic Regression')
plt.show()

在实现逻辑回归时，首先需要准备数据集，对数据集进行数据预处理和特征工程。然后，利用逻辑回归模型进行训练和预测。我们选择前两个特征，并对类别进行二分类，在代码中使用了StandardScaler进行特征缩放，将数据集划分为训练集和测试集。接下来，创建了一个逻辑回归模型，并在训练集上进行训练。最后，生成网格点坐标，并利用训练好的模型对网格点进行预测，将分类结果绘制成图像（如下图所示）。

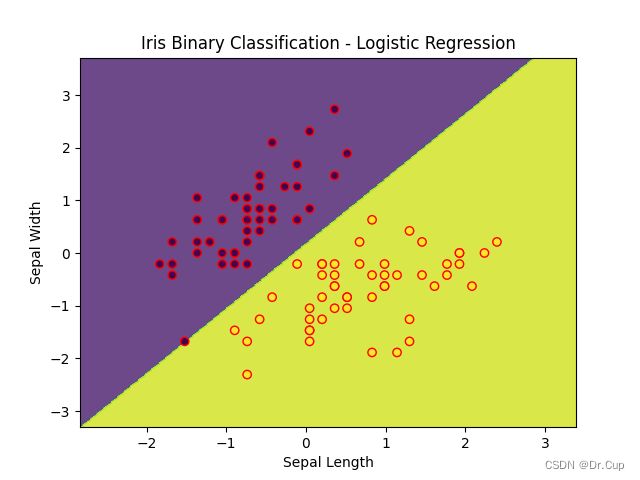
总结

逻辑回归是一个可以用于分类问题的机器学习算法。它通过将输入特征映射到概率值来进行分类预测，可以处理二分类和多分类问题。逻辑回归使用sigmoid函数进行映射，使用最大似然估计来求解参数向量。
总之，逻辑回归是一个简单而有效的分类算法，在解决分类问题时具有广泛的应用。它的原理简单清晰，实现也相对容易。如果文章存在其他问题，请随时提出，欢迎批评指正！