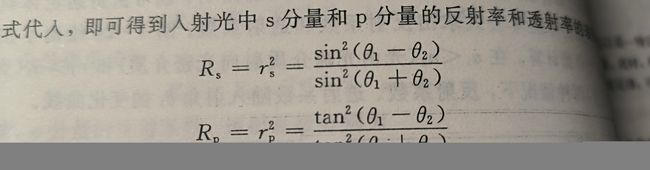python画图实例：根据函数关系画出反射率与入射角的曲线图

1.画图的第一步：找到函数关系建立数学模型。

 首先，观察函数关系，

 又有 *******       sinθ1=1.5*sinθ2      **********

这里我们把θ1作为x轴自变量，因此θ2也可以用θ1表示。Rs，Rp分别作为y1，y2的y轴因变量。

from matplotlib import pyplot as plt#导入函数命名为plt
from matplotlib import font_manager#为显示中文修改字体
import math             #下面会用到三角函数和弧度数

先导入matplotlib中的pyplot二维图库，这里画的二维图像。

2.画图要定义你的“纸”的大小，清晰度等等，然后才在画板上画图

figsize是画图板长宽的设置，单位为英寸。dpi是像素，值越大图越清晰，内存消耗也越多。

plt.figure(figsize=(20,8),dpi=80)            #画图板的设置

 3.根据数学模型写公式函数

这里我们用到的自变量的单位是角度，因此先要把x轴的单位转化成角度或者弧度数。我们这里利用radians将x返回为x°

方法：1.给x一个取值范围，利用for循环将所有x取值进行单位修改。（这里给1~90，对应就是1°~90°,。不能取0，因为下面函数如果x取0，则算出除数为0，会报错）

           2. 这里也可以使用角度计算，即θ=x/180*math.pi。总之必须转化为角度或者弧度数。

def jd(x):          #将数修改为弧度数返回
    radian=math.radians(x)
    return radian

for i in range(0,90):
    x[i]=jd(x[i])

*************************************************************************************************************

公式函数如下（对x每个值进行公式运算得到y1，y2，并依次添加到空列表中）：

其中m表示用x（即θ1）表示的θ2。a，b分别代表公式的分子和分母。对空列表逐一添加元素，m与y1，y2每个元素一一对应。

m=[]
y1=[]
y2=[]
for i in range(0,90):           #写公式函数
    m.append(math.asin((math.sin(x[i]))/1.5))
    a=(math.sin(x[i]-m[i]))**2
    b=(math.sin(x[i]+m[i]))**2
    y1.append(a/b)
plt.xlabel('入射角',fontproperties=my_font)
plt.ylabel('反射率R',fontproperties=my_font)

for i in range(0,90):
    m.append(math.asin((math.sin(x[i]))/1.5))
    a=(math.tan(x[i]-m[i]))**2
    b=(math.tan(x[i]+m[i]))**2
    y2.append(a/b)

这里格外写了一个xy轴的标题，一般来说标题不能带有中文，会显示乱码，但是通过修改字体来写中文则不会乱码。

4.在“纸”上画图，并展示出来

（若需要，设置x轴刻度，刻度不影响图像，只影响x轴刻度的显示。每隔多少单位显示一个刻度）

c=list(range(0,91))     #设置横坐标刻度值前，先写一个列表
for i in range(0,91):   #将即将设置的横坐标刻度值修改为弧度数单位
    c[i]=jd(c[i])
plt.xticks(c[::10],)    #设置横坐标刻度值，必须是列表，每10度一个刻度
plt.plot(x,y1)      #画x关于y1的图像，下同理
plt.plot(x,y2)
plt.show()              #展示图像

**************************************************************************************************************

全部代码为：

from matplotlib import pyplot as plt#导入函数命名为plt
from matplotlib import font_manager#为显示中文修改字体
import math             #下面会用到三角函数和弧度数
plt.figure(figsize=(20,8),dpi=80)            #画图板的设置
x=list(range(1,91))     #生成1，90的列表，（0不能做除数）
my_font=font_manager.FontProperties(fname="C:\Windows\Fonts\MSYHL.TTC")
def jd(x):          #将数修改为弧度数返回
    radian=math.radians(x)
    return radian
for i in range(0,90):
    x[i]=jd(x[i])
m=[]
y1=[]
y2=[]
for i in range(0,90):           #写公式函数
    m.append(math.asin((math.sin(x[i]))/1.5))
    a=(math.sin(x[i]-m[i]))**2
    b=(math.sin(x[i]+m[i]))**2
    y1.append(a/b)
plt.xlabel('入射角',fontproperties=my_font)
plt.ylabel('反射率R',fontproperties=my_font)

for i in range(0,90):
    m.append(math.asin((math.sin(x[i]))/1.5))
    a=(math.tan(x[i]-m[i]))**2
    b=(math.tan(x[i]+m[i]))**2
    y2.append(a/b)

c=list(range(0,91))     #设置横坐标刻度值前，先写一个列表
for i in range(0,91):   #将即将设置的横坐标刻度值修改为弧度数单位
    c[i]=jd(c[i])
plt.xticks(c[::10],)    #设置横坐标刻度值，必须是列表，每10度一个刻度
plt.plot(x,y1)      #画x关于y1的图像，下同理
plt.plot(x,y2)
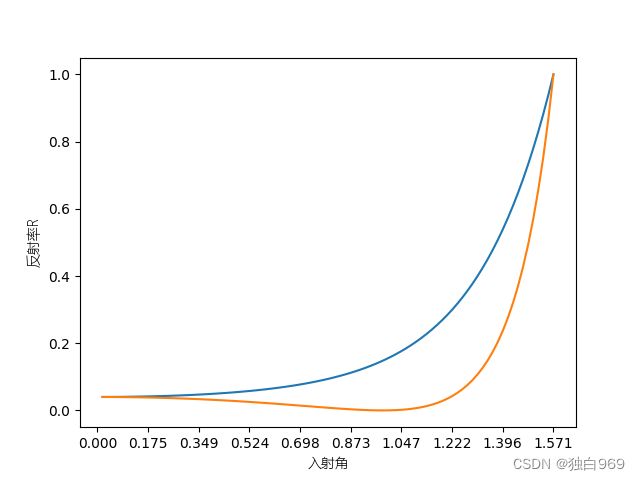
plt.show()              #展示图像

图像结果为：