今日arXiv最热NLP大模型论文:上海AI Lab联合清华发布十项全能数学大模型InternLM-Math
数学推理能力是大语言模型(LLMs)抽象推理能力的一个重要体现。近年来,随着深度学习技术的不断进步,LLMs在数学推理任务上取得了显著的进展。从小学级别到高中级别的数学问题,通过链式推理(chain-of-thought reasoning)或程序式推理(program-of-thought reasoning),LLMs展现出了解决数学问题的潜力。这些模型的构建需要在数学语料上进行预训练,并在数学问题上进行监督式微调。在这一背景下,该研究介绍了InternLM-Math,基于InternLM2-Base模型继续预训练的数学推理LLM。InternLM-Math不仅在解决数学问题方面表现出色,还在验证、证明和数据增强等多个方面展现了其能力。本文将对InternLM-Math的最新进展进行介绍,包括其在各项基准测试中的表现,以及如何通过开源的方式推动数学LLMs的发展。
论文标题:InternLM-Math: Open Math Large Language Models Toward Verifiable Reasoning
公众号「夕小瑶科技说」后台回复“InternLM-Math”获取论文链接。
InternLM-Math的核心能力与性能表现
InternLM-Math是从InternLM2继续预训练得到的,它整合了链式推理、奖励建模、形式推理、数据增强和代码解释器等多种能力于统一的序列到序列(seq2seq)格式中,并监督模型成为一个多功能的数学推理者、验证者、证明者和增强者。这些能力可以用于开发下一代数学LLMs或自我迭代。在不同的非正式和正式基准测试中,包括GSM8K、MATH、匈牙利数学考试、MathBench-ZH和MiniF2F等,InternLM-Math在上下文学习、监督式微调和代码辅助推理的设置下取得了开源领域的最佳性能。在没有微调的情况下,预训练的模型在MiniF2F测试集上达到了30.3的成绩。此外,研究团队还探索了如何使用LEAN来解决数学问题,并研究了在多任务学习设置下的性能表现,这表明了使用LEAN作为解决和证明数学问题的统一平台的可能性。
模型预训练:构建数学推理能力的基础
1. 预训练数据的组成与来源
模型预训练的数据来源多样,包括从公共语料库中检索的数学相关文本、特定领域数据集、以及合成的数学问题。例如,使用Query of CC检索系统从公共语料库中提取了20B个token的数学相关数据,同时还包括了来自开源数据集和高质量内部数据集的11B个token,这些数据涵盖了网页、代码、arXiv论文、论坛和书籍等内容。此外,为了提升模型的数值运算能力,还合成了包含算术、指数、对数、三角和多项式计算的数据,总计0.2B个token。
2. 数据后处理提升训练质量
为了提高训练数据的质量,采用了一系列的数据后处理策略。首先,训练了一个评分模型来识别高质量的数据集,然后使用Minhash-LSH方法对训练数据进行去重,过滤掉相似度超过0.7的重复数据。针对特定领域数据,还进行了精确公式去污染处理,例如,从MATH测试集中移除了所有与测试集中公式相匹配的数据。
3. 预训练策略与实施细节
在收集和后处理高质量数据后,设置了不同的训练周期。总共收集了31.2B个高质量token,大部分数据集使用4个epoch进行训练。预训练采用了InternLM2-Base模型,并使用InternEvo3作为训练框架。在训练过程中,使用了4096的上下文长度,对于过长或过短的文档进行截断或拼接。采用混合精度训练和FlashAttention技术优化内存利用和训练效率,使用标准的AdamW优化器,并设置了余弦学习率调度器。在预训练过程中,总共训练了125B个token,对于20B模型,基于上下文学习性能进行了80B token的提前停止。
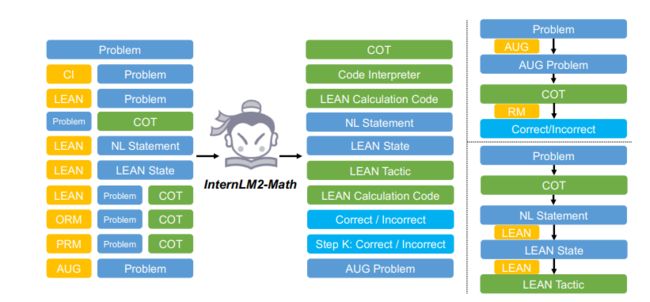
左侧部分显示了SFT中的查询和响应格式。右边的部分显示SFT模型的两种可能用途。右上角是使用增强助手、COT和RM能力合成新问题的渠道。右下角是使用具有COT和形式推理能力的形式语言解决非正式问题的渠道。
监督式微调(SFT):提升模型的数学解题能力
1. SFT数据构成与格式
SFT数据包含了高质量的人工编写、规则生成和LLM生成的数据,用于增强模型的数学解题能力以及自我提升所需的能力,如问题增强、奖励建模、自我验证、形式推理和代码解释器。
2. 链式推理(COT)在SFT中的应用
在SFT中,使用MetaMath作为英文链式推理的基础数据资源,并利用内部中文数据集来提升中文链式推理能力。为了改善模型在数学推理方面的弱点,对特定数据集应用了推理路径增强。此外,还引入了基本的数学能力,如检查素数、24点游戏、整数分解和计算三角形面积等。可以看下面这个例子。
3. 奖励模型(RM)的构建与应用
奖励模型有助于模型更好地对其生成进行重新排序并过滤合成数据以实现自我提升。受Math Shepherd启发,将ORM和PRM统一为seq2seq学习的相同格式,并添加了中文ORM数据。此外,还探索了使用LEAN作为解题器、验证器和证明器,通过将COT翻译成LEAN代码来验证推理路径的正确性。
代码解释器:增强模型的计算能力
1. 代码解释器的作用与集成方法
代码解释器能够增强大型语言模型(LLMs)在处理复杂计算任务时的能力。通过利用各种Python库,代码解释器为LLMs提供了灵活性和功能性。早期的尝试使用了程序化的思考策略,但这种方法不适用于需要多步推理和计算的场景,因为LLMs无法看到代码执行的结果。最近的工作尝试更加无缝地将代码解释器与推理过程集成,但这些方法不兼容并且需要对通用聊天服务进行额外修改。
InternLM-Math通过让LLMs进行交错的推理和编码(RICO),解决了上述问题。在这种设计中,LLMs以与聊天响应相同的格式进行推理,并采用通用的工具调用协议来使用代码解释器。这种设计不仅允许LLMs在使用代码解释器时充分发挥现有的推理能力,而且还允许模型在通用的工具增强系统中提供服务,这与GPT-4的工作方式更为相似。
具体来说,当回答一个数学问题时,模型被提示进行符号推理和程序生成,然后在每一轮中观察代码执行结果。模型将继续这样的轮次,直到在总结结果后完全回答问题,与之前的方法不同,这些方法本质上只写一次代码。推理过程使用与常规聊天响应相同的格式,而不是使用不同的标记来区分文本和代码。
2. 训练数据构建与迭代更新策略
为了构建数学代码解释器的训练数据,采用了迭代数据更新和难例挖掘策略,以减少对GPT-4的依赖。在每次迭代中,首先使用上一次迭代中训练的模型在GSM8K和MATH的训练集上生成响应。由于模型无法完全适应训练集,因此使用GPT-4-turbo在剩余的训练集上生成一次响应。最新模型和GPT-4-turbo生成的正确响应将被用来训练下一次迭代的新模型。初始数据由ToRA-70B生成,尽管格式不理想,但可以转换为正确的响应来训练初始模型。InternLM2-Chat和InternLM2-Math模型采用相同的训练数据来增强代码解释器能力。
实验结果与分析:验证预训练与SFT模型的性能
1. 预训练模型在标准数学推理基准上的表现
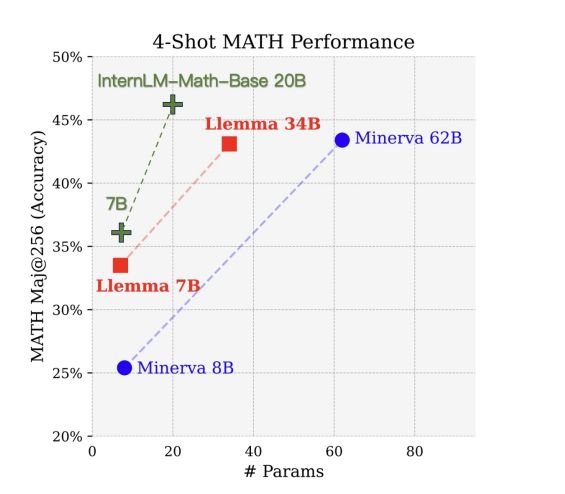
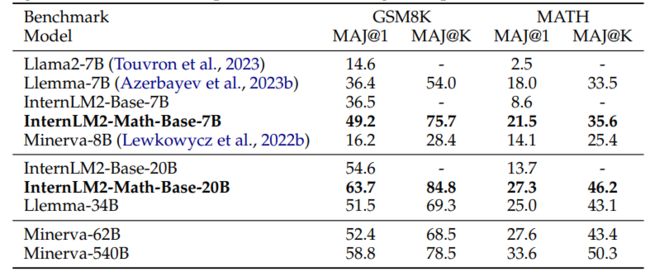
在标准的数学非形式推理基准GSM8K和MATH上,通过上下文学习评估预训练的基础模型的性能。使用OpenCompass的少数样本模板进行评估,并采用多数投票准确率作为评价指标。结果显示,InternLM2-Math-Base模型在两个基准测试中均优于其初始检查点InternLM2-Base,表明持续预训练的有效性。InternLM2-Math-Base-7B在MATH上获得了21.5的分数,优于Llemma-7B的18.0分。InternLM2-Math-Base-20B在MATH上获得了27.3的分数,与Llemma-34B相当,并且与规模更小的Minerva-62B表现相似。
2. SFT模型在各项数学推理任务上的表现
在GSM8K、MATH、匈牙利数学考试和MathBench-ZH上评估SFT模型的零样本链式推理能力。MathBench-ZH包含600个来自小学、中学、高中或大学级别的中文数学问题。对于MathBench-ZH中的每个选择题,将随机打乱选项顺序4次。一个模型如果能4次给出正确答案,则被认为是正确的。结果显示,InternLM2-Math-7B在GSM8K、MATH、匈牙利数学考试和MathBench-ZH上分别获得了78.1、34.6、55和40的分数,这表明在相同模型大小下,其在领域内和领域外的性能都更强。InternLM2-Math-20B在MATH和匈牙利数学考试上分别获得了37.7和66的分数,仅次于GPT-4。与Qwen-72B和DeepSeek-67B相比,它以更小的规模实现了最先进的性能。
模型的潜力与未来的自我提升路径
1. InternLM-Math在数学推理任务中的潜力
InternLM-Math作为基于InternLM2-Base模型的延续,通过在数学推理任务中的表现展示了其潜力。该模型不仅在解决数学问题上使用了链式推理(chain-of-thought, COT)和代码解释器,还在多任务开发数学LLMs中展现了多样的能力,包括奖励建模(reward modeling)和辅助数据增强(augment helper)。在多个非正式和正式的数学推理基准测试中,InternLM-Math取得了开源领域的最佳性能,例如在GSM8K、MATH、匈牙利数学考试、MathBench-ZH和MiniF2F等测试中均有出色表现。尤其是在MiniF2F测试集中,未经微调的预训练模型就达到了30.3的分数,显示了其在数学证明方面的潜力。
2. 模型自我提升的可能性与未来方向
InternLM-Math的设计不仅仅是为了解决数学问题,它还具备自我提升的潜力。模型整合了COT和数据增强助手的能力,可以用于合成新问题和新响应。同时,模型获得了ORM、PRM和LEAN的能力,可以用于验证生成响应的答案和过程。这种可验证的数据增强有望提高模型的能力。未来的自我提升路径可能包括进一步优化链式推理过程,减少模型在生成计算过程中的重复,并探索隐式链式推理的可能性。此外,模型还需要发展自我批判能力,以便更好地应用ORM或PRM,并解决由于SFT数据分布不均导致的代码切换问题。对于使用LEAN的SFT数据,未来的版本将转向使用更新的LEAN版本,以保持与最新的数学语言标准一致。
InternLM-Math的贡献与影响
InternLM-Math作为一种新型的数学推理大语言模型,为可验证的数学推理能力迈出了重要的一步。它在非正式和正式推理任务中展现出强大的性能,并且具备了自我提升的潜力。通过整合COT、奖励建模、数据增强助手、正式推理和代码解释器等多种能力,InternLM-Math不仅能够解决数学问题,还能够验证推理路径和证明数学陈述。这种模型的开源贡献,为未来的数学推理和自我迭代研究提供了宝贵的资源和启示。尽管InternLM-Math已经取得了显著的成就,但它仍然被视为自我提升的起点,未来的工作将致力于解决现有问题,并进一步提升模型的推理和验证能力。
公众号「夕小瑶科技说」后台回复“InternLM-Math”获取论文链接。