运筹系列35：凸优化接口cvxpy

1. 凸优化问题

1.1 QP问题

目标函数二阶，约束一阶，称为Quadratic programming

1.2. QCQP

目标二阶，约束二阶，Quadratical Constraint Quadratic Programming。

1.3. SOCP

second order cone program，本质上还是一个QP问题（约束条件进行平方）。

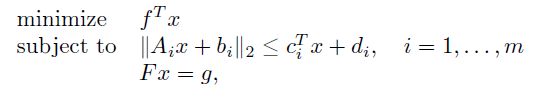
1.4 DCP

一个问题能够由目标函数和一系列约束构造。如果问题遵从DCP规则，这个问题将是凸的，能够被cvxpy解决。DCP规则要求目标函数有以下两种形式：

Minimize(convex)
Maximize(concave)
在DCP规则下的有效约束为：
affine == affine
convex <= concave
concave >= convex
你能调用object.is_dcp()来检查一个问题、约束、目标函数是否满足DCP规则。

2. Cvxpy介绍

CVXPY是一种可以内置于Python中的模型编程语言，解决凸优化问题。它可以自动转化问题为标准形式，调用解法器，解包结果集。下面是个简单的例子：

from cvxpy import *
x = Variable()
y = Variable()
constraints = [x + y == 1,
              x - y >= 1]
obj = Minimize(square(x - y))
prob = Problem(obj, constraints)
prob.solve()
print ("status:", prob.status)
print ("optimal value", prob.value) 
print ("optimal var", x.value, y.value) 

3. 其他求解器

在cvxpy默认的求解器不行时，我们要使用其他求解器，例如：

# Solving a problem with different solvers.
x = cvx.Variable(2)
obj = cvx.Minimize(x[0] + cvx.norm(x, 1))
constraints = [x >= 2]
prob = cvx.Problem(obj, constraints)

# Solve with ECOS.
prob.solve(solver=cvx.ECOS)
print("optimal value with ECOS:", prob.value)

# Solve with ECOS_BB.
prob.solve(solver=cvx.ECOS_BB)
print("optimal value with ECOS_BB:", prob.value)

# Solve with CVXOPT.
prob.solve(solver=cvx.CVXOPT)
print("optimal value with CVXOPT:", prob.value)

# Solve with SCS.
prob.solve(solver=cvx.SCS)
print("optimal value with SCS:", prob.value)

# Solve with GLPK.
prob.solve(solver=cvx.GLPK)
print("optimal value with GLPK:", prob.value)

# Solve with GLPK_MI.
prob.solve(solver=cvx.GLPK_MI)
print("optimal value with GLPK_MI:", prob.value)

# Solve with GUROBI.
prob.solve(solver=cvx.GUROBI)
print("optimal value with GUROBI:", prob.value)

# Solve with MOSEK.
prob.solve(solver=cvx.MOSEK)
print("optimal value with MOSEK:", prob.value)

# Solve with Elemental.
prob.solve(solver=cvx.ELEMENTAL)
print("optimal value with Elemental:", prob.value)

# Solve with CBC.
prob.solve(solver=cvx.CBC)
print("optimal value with CBC:", prob.value)
optimal value with ECOS: 5.99999999551
optimal value with ECOS_BB: 5.99999999551
optimal value with CVXOPT: 6.00000000512
optimal value with SCS: 6.00046055789
optimal value with GLPK: 6.0
optimal value with GLPK_MI: 6.0
optimal value with GUROBI: 6.0
optimal value with MOSEK: 6.0
optimal value with Elemental: 6.0000044085242727
optimal value with CBC: 6.0
//Use the installed_solvers utility function to get a list of the solvers your installation of CVXPY //supports.

print installed_solvers()
['CBC', 'CVXOPT', 'MOSEK', 'GLPK', 'GLPK_MI', 'ECOS_BB', 'ECOS', 'SCS'

直接用cvxopt求解的例子如下：

4. DPP

DPP是Disciplined Parametrized Programming (DPP)的缩写，即保持同样形状的问题。DPP中有一种新的数据格式叫parameter，要求固定变量variable后，对于parameters是一阶的（parameter-affine）。在这种情况下，用ECOS、SCS、MOSEK时可以加速。
下面是个例子：

import cvxpy as cp
m, n = 3, 2
x = cp.Variable((n, 1))
F = cp.Parameter((m, n))
G = cp.Parameter((m, n))
g = cp.Parameter((m, 1))
gamma = cp.Parameter(nonneg=True)
objective = cp.norm((F + G) @ x - g) + gamma * cp.norm(x)
print(objective.is_dcp(dpp=True))

开启dpp=Ture后，就可以给parameter输入不同的参数，反复求解问题了，下图是resolving的时间。