ABC338 A-E题解

A

题目

这个题就是看第一个字母是不是大写，其余的是不是小写就行了，挨个挨个判断就行了

AC Code：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
string s;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> s;
	bool flag = 1;
	if (!(s[0] >= 'A' && s[0] <= 'Z')) flag = 0;
	for (int i = 1; i < (int)s.size(); i ++) {
		if (!(s[i] >= 'a' && s[i] <= 'z')) flag = 0;
	}
	if (flag) cout << "Yes";
	else cout << "No";
	return 0;
}

B

题目

可以用一个数组记录每一个字母出现的次数，然后寻找最大值就行了。

AC Code：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
string s;
int cnt[120];

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> s;
	for (int i = 0; i < (int)s.size(); i ++) {
		cnt[(int)s[i] - 'a'] ++;
	}
	int maxx = 0, maxn;
	for (int i = 0; i < 26; i ++) {
		if (cnt[i] > maxx) {
			maxx = cnt[i];
			maxn = i;
		}
	}
	cout << char(maxn + 'a');
	return 0;
}

C

题目

这道题我们注意到 $N$ 特别的小。只有 $10$，所以我们可以枚举 A 菜品的个数，在判断冰箱里的配料是否足够，如果足够，在去判断最多能够制作多少个 B 菜品，然后寻找最大值就行了。

时间复杂度:$O(N)$，但是带一个 $10^6$ 的常数。

AC Code：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int n;
int q[20], a[20], b[20];
int ans;

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i ++) cin >> q[i];
	for (int i = 1; i <= n; i ++) cin >> a[i];
	for (int i = 1; i <= n; i ++) cin >> b[i];
	for (int i = 0; i <= 1000000; i ++) {
		int minn = 0x3f3f3f3f;
		int flag = 0;
		for (int j = 1; j <= n; j ++) {
			if (q[j] - a[j] * i < 0) flag = 1;
			if (b[j]) minn = min(minn, (q[j] - a[j] * i) / b[j]);
		}
		if (flag) break;
		ans = max(ans, minn + i);
	}
	cout << ans;
	return 0;
}

D

题目

对于从 $x$ 点到 $y$ 点一共就有两种走法，一种路径长度 $|x-y|$，另一种路径长度 $n-|x-y|$，我们选择短一点的那一条边走。

而如果较短路径上有一条边被破坏了，就只能走较长的那一条路径。

举个例子：

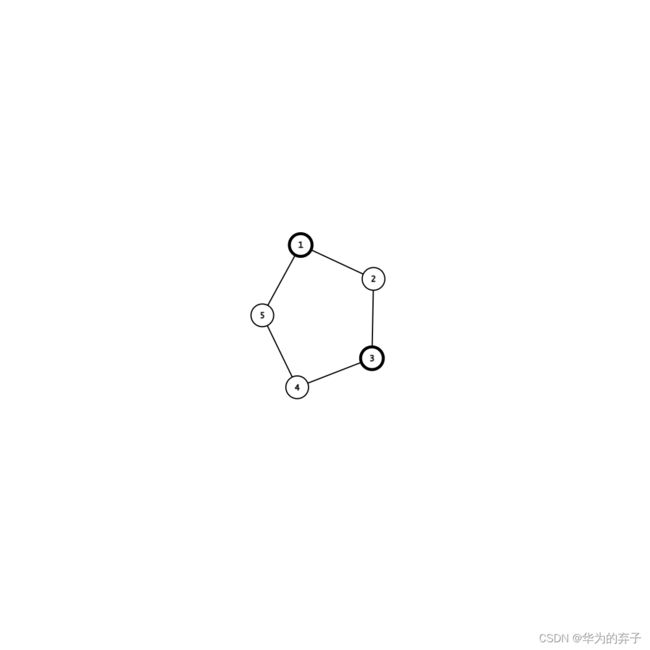
从 $1$ 走到 $3$ 的最短路径是从 $1$ 到 $2$ 再到 $3$。而如果第一条边，第二条边被破坏了，我们就只能走更长的那一条边，就要多走一条边。

所以我们可以枚举删了每一条边后，我们多走了多少条边，再加上原本我们应该走的那几条边，就是答案。

可以将所有的边都赋予一个权值，对于每一个起点和终点，他的路径上所有的边的权值都加上另外一条较长路径比较短路径多的边数。查询答案时，找权值最小的边加上本来的路径长度就行了。可以用差分维护边权数组，最后一并查询。

问题来了，图是一个环，而数组不是。如何处理环的问题？

这样如果较短路径是形如 $n-3,n-2,n-1,n,1,2,3$ 的路径时，就要特判一下，先标记从 起点 到 $n$，在从 $1$ 到终点。

时间复杂度 $O(n)$

AC Code：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int n, m;
int x[200100];
long long t[200100];
long long ans = 0x3f3f3f3f3f3f3f3f;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	for (int i = 1; i <= m; i ++) cin >> x[i];
	for (int i = 2; i <= m; i ++) {
		if (x[i] > x[i - 1]) {
			if (x[i] - x[i - 1] < n - (x[i] - x[i - 1])) {
				int k = n - (x[i] - x[i - 1]) - (x[i] - x[i - 1]);
				t[x[i - 1]] += k;
				t[x[i]] -= k;
			}
			else {
				int k = x[i] - x[i - 1] - (n - (x[i] - x[i - 1]));
				t[1] += k;
				t[x[i - 1]] -= k;
				t[x[i]] += k;
				t[n + 1] -= k;
			}
		}
		else {
			if (x[i - 1] - x[i] < n - (x[i - 1] - x[i])) {
				int k = n - (x[i - 1] - x[i]) - (x[i - 1] - x[i]);
				t[x[i]] += k;
				t[x[i - 1]] -= k;
			}
			else {
				int k = x[i - 1] - x[i] - (n - (x[i - 1] - x[i]));
				t[1] += k;
				t[x[i]] -= k;
				t[x[i - 1]] += k;
				t[n + 1] -= k;
			}
		}
	}
	long long tmp = 0;
	for (int i = 2; i <= m; i ++) tmp += min(n - abs(x[i] - x[i - 1]), abs(x[i] - x[i - 1]));
	long long sum = 0;
	for (int i = 1; i <= n; i ++) {
		sum += t[i];
		ans = min(ans, sum);
	}
	cout << ans + tmp;
	return 0;
}

E

题目

将这个问题抽象成区间问题，就是给定一些区间，求有没有两个区间，他们有部分交际但是各自都不被对方包含。

我们先将区间按左端点排序，然后倒着遍历区间，定义一个数组 $t$，第 $i$ 项代表它被其他区间包含的区间个数，设我们当前处理的区间右端点为 $x$，如果 $t_x\ge 1$，就代表右端点被某个区间包含，又因为是倒着处理，我们当前处理区间的左端点一定比相交的区间的左端点靠左，所以就代表我们找到了与当前区间相交的区间，输出 Yes走人，否则，我们就标记上这个区间，继续处理下一个区间。如果处理完所有区间都还没有找到的话，就输出 No。
$t$ 数组用差分维护，可以用线段树或树状数组维护差分，我选用了线段树。

时间复杂度：$O(n\times lo{g}_2(n))$

AC Code：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int n;
struct node1{
	int a, b;
};
node1 a[200100];
bool cmp(node1 a, node1 b) {
	if (a.a == b.a) return a.b < b.b;
	return a.a < b.a;
}
struct node{
	int l, r, sum;
};
node t[3200100];
void maketree(int l, int r, int p) {
	t[p].l = l;
	t[p].r = r;
	if (l < r) {
		maketree(l, (l + r) / 2, p * 2);
		maketree((l + r) / 2 + 1, r, p * 2 + 1);
	}
}
void add(int i, int k, int p) {
	if (t[p].l <= i && t[p].r >= i) t[p].sum += k;
	else return ;
	add(i, k, p * 2);
	add(i, k, p * 2 + 1);
}
int get(int l, int r, int p) {
	if (t[p].l >= l && t[p].r <= r) return t[p].sum;
	if (t[p].l > r || t[p].r < l) return 0;
	return get(l, r, p * 2) + get(l, r, p * 2 + 1);
}

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i ++) {
		cin >> a[i].a >> a[i].b;
		if (a[i].a > a[i].b) swap(a[i].a, a[i].b);
	}
	maketree(1, n * 2, 1);
	sort(a + 1, a + n + 1, cmp);
	for (int i = n; i >= 1; i --) {
		if (get(a[i].b, n * 2, 1)) {
			cout << "Yes";
			return 0;
		}
		add(a[i].b, 1, 1);
		add(a[i].a, -1, 1);
//		for (int j = 1; j <= n * 2; j ++) cout << get(j, j, 1) << ' ';
//		cout << '\n';
	}
	cout << "No";
	return 0;
}