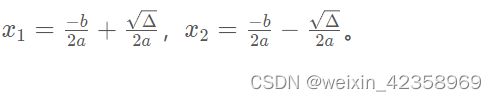2023年CSP-J复赛真题解析

2023年CSP-J-T1-小苹果（apple）

题目描述

小Y的桌子上放着n个苹果从左到右排成一列，编号为从1到n。

小苞是小Y的好朋友，每天她都会从中拿走一些苹果。

每天在拿的时候，小苞都是从左侧第1个苹果开始、每隔2个苹果拿走1个苹果。

随后小苞会将剩下的苹果按原先的顺序重新排成一列。

小苞想知道，多少天能拿完所有的苹果，而编号为n的苹果是在第几天被拿走的？

输入格式

从文件apple.in中读入数据。

输入的第一行包含一个正整数，表示苹果的总数。

输出格式

输出到文件apple.out中。

输出一行包含两个正整数，两个整数之间由一个空格隔开，分别表示小苞拿走所有苹果所需的天数以及拿走编号为n的苹果是在第几天。

输入输出样例

输入样例1：

8

输出样例1：

5 5

说明

样例1解释：

小苞的桌上一共放了8个苹果。

小苞第一天拿走了编号为1、4、7的苹果。

小苞第二天拿走了编号为2、6的苹果。

小苞第三天拿走了编号为3的苹果。

小苞第四天拿走了编号为5的苹果。

小苞第五天拿走了编号为8的苹果。

数据范围：

对于所有测试数据有：1 ≤ n ≤ 10^9。

特殊性质：小苞第一天就取走编号为n的苹果。

耗时限制1000ms   内存限制512MB

解析

考点：数学

90 分解法：

类似约瑟夫问题的模拟去标记处理，对于 90% 的测试数据，n≤10^6，开一个 10^6\数组即可做标记。然后循环处理标记数组，因为每一轮都会去掉 1/3 的苹果。因此最多循环 log3/2​10^6 次。

思路分析：

找规律的题。题目有两问：

1. 苹果什么时候拿完？
2. 编号为 n 的苹果是在第几轮被拿走的？

对于第一问，容易发现，按拿走的规则看，每三个苹果就会拿走一个苹果。因此，每一轮拿走的苹果数量是⌈n/3⌉。也就是每次都至少拿走三分之一的苹果。如此，我们可以直接循环修改 n 并计数，就可以在 O(log2/3​​n) 时间复杂度下求出第一问。

对于第二问，容易发现，编号为 n 的苹果只要在当前一轮中没有被拿走，那么在下一轮中，它仍旧是最后一个苹果。对于 n 号苹果，如果它所在的位置 mod3 为 1，那么就会被拿走。因此，我们在第一问的循环修改中直接判断 n 即可确定 n 号苹果是在第几轮被拿走的。

时间复杂度：O(log2/3​​n)

参考代码：

#include
using namespace std;

int n, day, ans;

int main(){
    cin >> n;
    int m = n;  // 当前苹果数量
    while(m) {  // n 号苹果在每一轮都是最后一个苹果，也就是第 m 个苹果
        day++;
        if(m%3==1 && !ans) ans = day; // n 号个苹果在这一天被拿走
        m -= (m+3-1)/3;  // 向上取整
    }
    cout << day << ' ' << ans;
    return 0;
}

2023年CSP-J-T2-J 公路（road）

题目描述

小苞准备开着车沿着公路自驾。

公路上一共有 n 个站点，编号为从 1 到 n。 其中站点i与站点 i + 1 的距离为vi公里。

公路上每个站点都可以加油，编号为 i 的站点一升油的价格为ai元，且每个站点只出售整数升的油。

小苞想从站点 1 开车到站点 n，一开始小苞在站点 1 且车的油箱是空的。已知车的油箱足够大，可以装下任意多的油，且每升油可以让车前进d公里。

问小苞从站点 1 开到站点 n，至少要花多少钱加油？

输入格式

从文件road.in中读入数据。

输入的第一行包含两个正整数 n 和 d, 分别表示公路上站点的数量和车每升油可以前进的距离。

输入的第二行包含 n - 1 个正整数v1, v2 . . . vn-1,分别表示站点间的距离。

输入的第三行包含n个正整数 a1, a2. ... an, 分别表示在不同站点加油的价格。

输出格式

输出到文件road.out中。

输出一行，仅包含一个正整数，表示从站点1开到站点，小苞至少要花多少钱加油。

输入输出样例

输入样例1：

5 4 
10 10 10 10 
9 8 9 6 5

输出样例1：

79

说明

【样例1解释】

最优方案下：小苞在站点1买了3升油，在站点2购买了5升油，在站点4购买

了2升油。

【数据范围】

对于所有测试数据保证：1 ≤ n ≤ 10^5，1 ≤ d ≤ 10^5，1 ≤ vi ≤ 10^5，1 ≤ ai ≤10^5。

特殊性质A: 站点1的油价最低。

特殊性质B: 对于所有 1 ≤ i < n, vi 为 d 的倍数。

耗时限制1000ms   内存限制512MB

解析

考点：贪心

由于油箱容量无限大，因此容易发现，从 i 号站点走到 i+1 号站点这一段路，我们需要的油可以从前 i 个站点去购买。其实就相当于在i 号站点买油需要花费的代价是前 i 个站点买油所需要的最小值。

接下来，我们就按照刚才这个性质进行模拟每次从当前站点买够刚好能走到下一个站点的油就可以了。

实现时，要注意，由于必须购买整数升的汽油，因此跑到一个新站点后汽油是可能有剩余的，因此要注意保存剩余能跑的里程数。

参考代码：

#include
using namespace std;

const int N = 1e5+5;
int n, d, a[N], v[N], mi = 1e9;
long long ans, dis, sum; // dis: 当前总共跑的里程，sum：当前加的油能跑的里程
int main(){
    cin >> n >> d;
    for(int i = 1; i < n; i++) cin >> v[i];
    for(int i = 1; i < n; i++) {
        cin >> a[i];
        mi = min(mi, a[i]);
        dis += v[i]; // 当前总里程
        if(dis < sum) continue; // 坑点，可能剩余的油够到下一个站点，不需加油
        long long oil = (dis-sum+d-1)/d;  // 需要再加的油
        sum += oil * d;   // 当前总共加的油能够走的里程数
        ans += oil * mi;  // 总花费
    }
    cout << ans;
    return 0;
}

2023年CSP-J-T3-一元二次方程（uqe）

题目描述

题目背景：

题目描述：

输入格式

从文件 uqe.in 中读入数据。

输入的第一行包含两个正整数T, M,分别表示方程数和系数绝对值的上界：

接下来T行，每行包含三个整数a, b, c。

输出格式

输出到文件uqe.out中。

输出T行，每行包含一个字符串，表示对应询问的答案，格式如题面所述。

每行输出的字符串中间不应包含任何空格。

输入输出样例

输入样例1：

9 1000
1 -1 0
-1 -1 -1
1 -2 1
1 5 4
4 4 1
1 0 -432
1 -3 1
2 -4 1
1 7 1

输出样例1：

1
NO
1
-1
-1/2
12*sqrt(3)
3/2+sqrt(5)/2
1+sqrt(2)/2
-7/2+3*sqrt(5)/2

说明

数据范围：

耗时限制1000ms  内存限制512MB

解析

考点：数学，数论

纯模拟题，按照题意实现即可，即使不懂二次方程求根公式也没事，反正该给的信息他都给了，只需认真读题。

实在理解不了求根公式的话，可以针对“特殊性质 C” 来骗分，代入所有 [−2000,2000] 的整数来判断是否有解，以及求最大的解，这样可以得到 50 分：

参考代码

#include
using namespace std;
int main() {
    int _;
    scanf("%d%*d", &_);
    while (_--) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        int ans, ok = 0;
        for (int i = -2000; i <= 2000; i++) {
            if (a * i * i + b * i + c == 0) ans = i, ok = 1;
        }
        if (ok)
            printf("%d\n", ans);
        else
            puts("NO");
    }
    return 0;
}

100分做法

根据题意，我们可以知道对于一元二次方程ax^2+bx+c=0，Δ=Δ=b2−4ac。

1. 当 Δ<0 时，方程无实数解直接输出 NO。
2. 当 Δ≥0 时,方程两个解分别为:
3. 当 a<0 时，我们会发现最大的实数解是 x2​。当 a>0 时，最大的实数解是x1​。 

然后我们按照上面部分分的思路分析讨论：

1. 当 Δ是整数时，只需带入计算，此时做法和讨论性质 B 一致。
2. 当 Δ​ 不是整数时，此时做法和讨论性质 A 类似，我们需要化简 Δ​，只需枚举 1^2∼(5 m)^2
3. 时间复杂度O(TM)
4. 参考代码：

#include
using namespace std;

int T, M, x[3005];
// p*sqrt(x)/q 转字符串输出
string expr(int p, int q, int x) {
    string res;
    if(p == 0) return "0";  // 特判 0
    bool f = (p*q<0);
    p = abs(p); q = abs(q);
    int g = __gcd(p, q);
    p /= g; q /= g;
    if(f) res += "-";
    if(x == 0) {  // 不带根号
        res += to_string(p);
    } else {
        if(p != 1) res += to_string(p) + "*";
        res += "sqrt(" + to_string(x) + ")";
    }
    if(q != 1) {
        res += "/" + to_string(q);
    } 
    return res;
}
int main(){
    
    cin >> T >> M;
    for(int i = 1; i < 3005; i++) x[i] = i*i;
    while(T--) {
        int a, b, c;
        cin >> a >> b >> c;
        int d = b*b - 4*a*c;  // delta
        if(b == 0 && c == 0) {
            cout << "0\n";
            continue;
        }
        int rt = sqrt(d);
        if(d < 0) {  // 无解
            cout << "NO\n";
        }  else if(d == 0) {
            cout << expr(-b, 2*a, 0) << '\n';  
        } else {  // 有实数解
            if(rt*rt == d) {  // 有有理数解
                if(a < 0)
                    cout << expr(-b-rt, 2*a, 0) << '\n';
                else
                    cout << expr(-b+rt, 2*a, 0) << '\n';
            } else {  // 无理数解
                string q1 = expr(-b, 2*a, 0);  // -b/(2*a)
                // 化简 + sqrt(d)/(2*|a|)
                int p = 1, q = 2*abs(a);
                // 不论 a正负，sqrt(d) / (2*a) 前一定是 + 号
                int g = 0;
                for(int i = 3000; i >= 1; i--) {
                    if(d % x[i] == 0) {
                        g = i;
                        break;
                    }
                }
                if(g) {  // d 可化简
                    p = g;
                    d /= x[g];
                }
                string q2 = expr(p, q, d);
                if(q1 != "0") cout << q1 << "+";
                cout << q2 << '\n';
            }
        }
    }
    return 0;
}

2023年CSP-J-T4-旅游巴士（bus）

题目描述

       小 Z 打算在国庆假期期间搭乘旅游巴士去一处他向往已久的景点旅游。

旅游景点的地图共有 n 处地点，在这些地点之间连有 m 条道路。其中1号地点为景区入口，n号地点为景区出口。我们把一天当中景区开门营业的时间记为 0 时刻，则从 0 时刻起，每间隔 k 单位时间便有一辆旅游巴士到达景区入口，同时有一辆旅游巴士从景区出口驶离景区。

       所有道路均只能单向通行。对于每条道路，游客步行通过的用时均为恰好 1 单位时间。

       小 Z 希望乘坐旅游巴士到达景区入口，并沿着自己选择的任意路径走到景区出口，再乘坐旅游巴士离开，这意味着他到达和离开景区的时间都必须是 k 的非负整数倍。由

于节假日客流众多，小 Z 在坐旅游巴士离开景区前只想一直沿着景区道路移动，而不想在任何地点（包括景区入口和出口）或者道路上逗留。

       出发前，小 Z 忽然得知：景区采取了限制客流的方法，对于每条道路均设置了一个“开放时间”，游客只有不早于 ai，时刻才能通过这条道路。

       请你帮助小 Z 设计一个旅游方案，使得他乘坐旅游巴士离开景区的时间尽量地早。

输入格式

从文件bus.in中读入数据。

输入的第一行包含3个正整数n,m,k, 表示旅游景点的地点数、道路数，以及旅游巴士的发车间隔。

输入的接下来m行，每行包含3个非负整数ui, vi, ai, 表示第 i 条道路从地点ui出发，到达地点vi，道路的“开放时间”为ai。

输出格式

输出到文件bus.out中。

输出一行，仅包含一个整数，表示小 Z 最早乘坐旅游巴士离开景区的时刻。如果不存在符合要求的旅游方案，输出 -1。

输入输出样例

输入样例1：

5 5 3
1 2 0
2 5 1
1 3 0
3 4 3
4 5 1

输出样例1：

6

说明

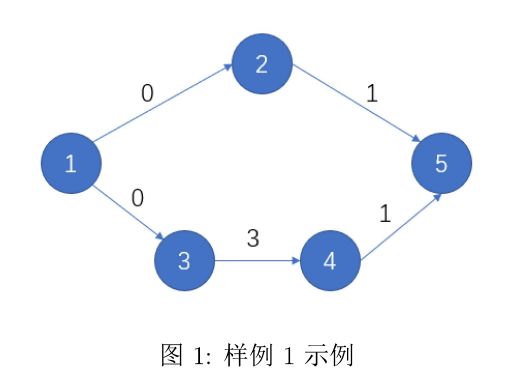
【样例1解释】

小 Z 可以在 3 时刻到达景区入口，沿1 -> 3 -> 4 -> 5的顺序走到景区出口，并在6时刻离开。

【数据范围】

对于所有测试数据有：2 ≤ n ≤ 10^4, 1 ≤ m ≤ 2 × 10^4, 1 ≤ k ≤ 100, 1 ≤ ui, vi ≤ n, 0 ≤ ai ≤10^6

耗时限制1000ms   内存限制512MB

解析

考点：分层图，最短路

题目大意：

给定一个有 n 个点，m 条边的有向图，点 1 为入口，点 n 为出口，从 0时刻起，可以到达入口进入图，也可以从出口离开。

你可以在图上花 1 个单位时间，从一条有向边的起点 ui​ 走到终点vi​，但不能在点和边上花时间逗留。且第 i 条边只有在当前时刻 ≥ai​ 时，才能够走过这条道路。

从入口进入图和从出口离开图的时刻都需要是 k 的倍数，求最早的离开图的时间，无解输出 −1。

10 分做法：

k≤1，ai​=0

第 6,76,7 两个数据点满足这一性质，此时即有 k=1。结合题意，这部分数据的特殊性质是: 任意时刻都可以进入或离开图且边的行走没有时刻限制。

我们可以将走过每条边所需的一个单位时间当做是这条边的长度，此时，问题就变成了从点 1 走到点 n，求最短路长度的经典问题，可以使用 BFS 解决。这是一个图上广搜，使用邻接表存图可以做到 O(n+m) 的时空复杂度。

25分做法:

k≤1

还有第 8∼10 组数据满足k=1 的条件，此时要考虑走过每条边的时刻限制了。是不是只需要对于上面 10 分做法的 BFS额外对比行走时的当前时间和每条边的时刻限制，就可以了呢？

上面的一个简单例子即可说明 BFS 做法的漏洞: 当k=2 时，从点 1 开始 BFS，则到达点 2 的最早时刻为 d2=1￥，此时从点2到点到点3的边要求时刻的边要求时刻≥ 5，所以普通的BFS只能终止，最终当做无解情形处理。但若在时刻，所以普通的BFS只能终止，最终当做无解情形处理。但若在时刻4从点从点1出发，则时刻出发，则时刻6即可到达点即可到达点3$，所以，我们需要考虑在边的行走出现限制时如何处理。

注意到 k=1，即任何时刻都可以进入/离开图，因此，对于有向边(ui​,vi​,ai​)，即使 dui​​

dvi​​=max(dui​​,ai​)+1

这一计算最短路的方式不能用 BFS 简单解决，可以使用 SPFA 等算法解决一般情形下 (即边长不固定为 11) 的图上最短路问题，但已经略微超过入门组的考纲范围。

35 分做法:

ai​=0

数据范围中的第 1∼2，6∼7，11∼13代表着另一块难以解决的部分ai​=0，但 k 未必为 1。当进入/离开图的时间必须为k 的倍数时，如何解决问题？

我们已经在学习 DP 时，面对过类似的问题，这些问题都要求某种元素之和要为 k 的倍数。

而一个数为 k 的倍数，等价于这个数除以 k 的余数为 0。所以，在处理之前的问题时，我们可以给 DP 数组增加一维表示元素之和除以 k 的余数。这样做需要将数组也开大对应 k 倍，因此这类问题的 k 都不会太大，而刚好在这一问题中 k≤100。

因此，对于ai​=0 时的普通 BFS 问题，我们可以对最短路数组稍作修改: 记 dj,j​ 表示到达了点u，且花费时间除以 k 的余数为 j 的最少时间花费，则对于有向边 (u,v) 有如下转移：

dv,(j+1)%k​=du,j​+1

我们可以基于下图更好地理解这一做法：走到一个点所用的最短时间，根据花费总时间模 k 的余数，有 0,1,2,...,k−1 这 k 种不同的情况，因此每个原图中的点可以按照时间模 k 的余数来分成 k 个不同的版本，得到一个共有 n×k 个点的新图。

设上图中 k=2，原图中的有向边 (1,3)，可以使得花费时间因此会从第 0 层的点 1 转移到第 1 层的点 3，但这并不是真正地在原图中到达了点 3，因为进入图和离开图的时刻都要是 k 的倍数，且只能一刻不停地在图中行走，所以在图上花费的时间也要是 k 的倍数，即在新图中，要从第 0 层的点 1 走到第 0 层的点 k。而原图中的有向边 (1,2)，可以使得第 0 层的点 1 转移到第 1 层的点 2，有向边 (1,2) 又可以使得第 1 层的点 2 转移到第 (1+1) 层的点 3，恰好是一条符合要求的路径。

这一种处理问题的方法，称为分层图，时空复杂度取决于分层图中的点数和边数。核心代码如下：

struct Edge{ int v, w; };
vector g[N];
int dis[N][105];  // dis[u][d]: 以 mod k=u 的时刻到达结点 u 的最小时间
void bfs(int s) {
    memset(dis, 0x3f, sizeof dis);
    queue q;
    dis[1][0] = 0;
    q.push({1, 0});
    while(!q.empty()) {
        int u = q.front().v, w = q.front().w;
        q.pop();
        for(auto e : g[u]) {
            int p = w + 1;  // 距离+1，不用考虑 a_i
            if(dis[e.v][p%k] != 0x3f3f3f3f) continue;
            dis[e.v][p%k] = dis[u][w%k]+1;
            q.push({e.v, p});
        }
    }
}

100 分做法：

要循序递进至满分做法，我们仍然需要使用分层图。假设问题考虑的情形有解，则我们可以想象: 时刻 0 时，大多数边还无法通行，不能从点 1 走到点 n，而时刻足够大后，所有边都可以通行，从点 1 到点 n 的花费时间不再随着时刻增加而改变这中间就存在一个“临界点”早于这个时刻出发则无法到达点 n。晚于这个时刻出发则可以让出发时间再提早 k，到达时间只会更早。

有解题经验的同学已经能够看出: 可以二分答案，也就是一分到达的时间，将求解性问题转化为判断性问题。代码实现上我们并非要二分到达的确切时刻，因为时刻只能是 k 的倍数在二分区间中是离散的，不便于二分，我们可以转而二分到达时刻除以 k 的商，也就是倍数，有解时，用二分得到的最小倍数乘以 k 即为答案。

二分到达时间除以k 的商 mid，则实际到达点 n 时间为 mid∗k，我们只需判断能否在时刻mid∗k 之前到达点 n，这仍然需要在分层图中进行 BFS，但多了一处细节要考虑：如何判断当前是否可以走过一条有向边? 这里不能再用 BFS 了，因为边的最早通过时间ai​ 破坏了 BFS 的最短路性质。但我们仍然可以使用 25 分中的改变最短路计算式的方法，但这需要引入 SPFA、Diikstra 等图上最短路算法，已经超出了入门组的考察范围【参考代码见最后】。

其实，我们可以将整个有向图反向，从终点反向 BFS，此时最短路数组表示的含义也有所不同：dv,j​ 改为表示从点 v 出发到达终点 n，路上花费时间除以 k 的余数为 j 的最少时间花费。初始时，dn,0​=mid∗k。则对于原图中的有向边(u,v) 有如下转移：

du,(j−1+k)%k​=dv,j​−1

请注意这一转移与 35 分做法中的转移的区别。BFS 后，可以根据 d1,0​ 的值判断能否在 mid∗k 时间内从点 11 走到点 n。

分层图的 BFS 与 35 分做法类似,只是将这一过程当做了二分内的处理，因此空间复杂度不变，时间复杂度需要乘上一个 log 因子。至于二分的答案区间起始值，可以从分层图 BFS 得到的最短路最大值来考虑：m 条边在分层图中会出现 m 次，则分层图的最长链长度不超过 mk，故二分区间的右端点取r=2×10^6 即可。

/*
二分+分层图bfs 的写法不可以二分最早的起始时刻。原因如下：

bfs 求的是最短路，但是二分的时候目标是从 mid*k 时刻从 1 点出发，**能否** 到达 n 点。

从 u -> v 的最短路受开放时间的限制，如果是不可行的，这条路就不会再走了，而确实可以”绕路“过去，但是绕路过去的最优方案就无法用bfs求解了，因为没法判断一个绕路的方案是否是最优的，只能继续接着找其他绕路的。

而二分到达时刻却可以，此时如果时间 >= a[i]，则意味对应的边可走，且一定是最优的。因为到达时间已经确定了。

*/
#include 
using namespace std;

const int N = 1e4+5;
int n, m, k;
struct Edge{ int v, w; };
vector g[N];
int dis[N][105];
bool bfs(int mid) {
    memset(dis, -1, sizeof dis);
    dis[n][0] = mid*k;
    queue q;
    q.push({n, 0});
    while(!q.empty()) {
        int u = q.front().v;
        int d = q.front().w;
        q.pop();
        if(dis[u][d] == 0) continue; // 时间不能早于 0
        for(auto e : g[u]) {
            if(e.w >= dis[u][d]) continue;  // 路径未到开放时间
            int t = (d - 1 + k) % k;
            if(dis[e.v][t] == -1) {
                dis[e.v][t] = dis[u][d] - 1;
                q.push({e.v, t});
            }
        }
    }
    return dis[1][0] != -1;
}
int main(){
    
    cin >> n >> m >> k;
    for(int i = 1, u,v,w; i <= m; i++) {
        cin >> u >> v >> w;
        g[v].push_back({u,w});
    }
    int l = 0, r = 2e6, mid, ans = -1;
    while(l <= r) {
        mid = (l+r) / 2;
        if(bfs(mid)) {
            ans = mid;
            r = mid-1;
        } else
            l = mid+1;
    }
    if(ans != -1) ans *= k;
    cout << ans;
    return 0;
}

另一种 100 分写法：

对于学过最短路的同学，可以不再使用二分法，而是把分层图和最短路结合起来，写法类似两种暴力算法 (ai​ 等于 0、k 等于 1) 的结合。由于最短路不是入门组的考纲，这里不再详细描述，请结合下方的代码理解。

#include 
using namespace std;

const int N = 1e4+5;
int n, m, k;
struct Edge{ int v, w; };
vector g[N];
int dis[N][105];  // dis[u][d]: 以 mod k=u 的时刻到达结点 u 的最小时间
bool vis[N][105];
void spfa(int s) {
    memset(dis, 0x3f, sizeof dis);
    dis[1][0] = 0; vis[1][0] = 1;
    queue q;
    q.push({1, 0});
    while(!q.empty()) {
        int u = q.front().v, w = q.front().w;
        q.pop();
        vis[u][w] = 0;
        for(auto e : g[u]) {
            int p = (w+1)%k;
            int tim = dis[u][w];  // 从 u 出发去 e.v 的最早时刻
            if(dis[u][w] < e.w) { // 无法通行
                // 只能通过在入口晚 k 倍时间出发使到达此结点时可通行
                //  tim += (e.w + k - 1 - tim)/k *k;
                tim += ceil((1.0*e.w-tim)/k) * k;
            }
            if(dis[e.v][p] <= tim + 1) continue;  // 不是最短路
            dis[e.v][p] = tim + 1;
            if(!vis[e.v][p]) {
                vis[e.v][p] = 1;
                q.push({e.v, p});
            }
        }
    }
}
void dij(int s) {
    memset(dis, 0x3f, sizeof dis);
    dis[1][0] = 0;
    priority_queue> q;
    q.push(make_pair(0, 1));
    while(!q.empty()) {
        int u = q.top().second, w = -q.top().first;
        int p = w%k;
        q.pop();
        if(vis[u][p]) continue;
        vis[u][p] = 1;
        for(auto e : g[u]) {
            int tim = dis[u][p] + 1;  // 从 u 出发到达 e.v 的最早时刻
            if(dis[u][p] < e.w) { // 无法通行
                // 只能通过在入口晚 k 倍时间出发使到达此结点时可通行
                tim += (e.w + k - 1 - dis[u][p])/k *k;
                //tim += ceil((1.0*e.w-tim)/k) * k;
            }
            if(dis[e.v][tim%k] <= tim) continue;
            dis[e.v][tim%k] = tim;
            q.push(make_pair(-tim, e.v));
        }
    }
}
int main(){
    cin >> n >> m >> k;
    for(int i = 1, u,v,w; i <= m; i++) {
        cin >> u >> v >> w;
        g[u].push_back({v,w});
    }
    dij(1);  // spfa(1);
    if(dis[n][0] == 0x3f3f3f3f) dis[n][0] = -1;
    cout << dis[n][0];
    return 0;
}