趣学贝叶斯统计:概率密度分布(probability density function)
目录
-
- 1. 分布:PDF与PMF
-
- PMF
- 2. 将概率密度函数应用于我们的问题
- 用积分量化连续分布
-
- 积分
- 度量变化率:导数
- 3. R语言实践
- 4. 小结
1. 分布:PDF与PMF
PDF定义在连续值上。在连续型随机变量的情况下,具体取某个数值的概率是0,因此PDF并不直接给出某个点的概率,而是给出了在某个区间内随机变量出现的概率密度。在数学上,PDF就是定义在连续值上的概率密度函数。
概率密度函数(probability density function,PDF): β \beta β 分布
B e t a ( p ; a , b ) = p a − 1 ⋅ ( 1 − p ) b − 1 B ( a , b ) Beta(p;a,b) = \frac{p^{a-1} \cdot (1-p)^{b-1}}{B(a, b)} Beta(p;a,b)=B(a,b)pa−1⋅(1−p)b−1
其中, 0 ≤ x ≤ 1 0\leq x \leq 1 0≤x≤1, a > b > 0 a \gt b \gt 0 a>b>0。
p: 事件概率。黑盒子吐出两枚硬币可能概率的不同假设。
a:观察到的时间次数。黑盒子吐出两枚硬币。
b:事件不发生的次数。黑盒子吞掉硬币的次数。
实验总次数:a+b。
PMF
PMF实验总次数是n, k是感兴趣的发生次数。
注意:分子不一样。
f ( k ∣ n , p ) = ( n k ) p k ( 1 − p ) n − k f(k|n,p) = \binom{n}{k} p^k (1-p)^{n-k} f(k∣n,p)=(kn)pk(1−p)n−k
PMF分子是 p k ( 1 − p ) n − k p^k (1-p)^{n-k} pk(1−p)n−k
PDF分子是 p a − 1 ⋅ ( 1 − p ) b − 1 p^{a-1} \cdot (1-p)^{b-1} pa−1⋅(1−p)b−1,指数项需要分别减1。我们从指数项中减去1,并使用beta函数归一化所得的值——这可以确保分布之和为1。
我们最后得到了这样一个函数:它描述的是每个可能假设的概率,这些假设是我们相信从盒子里得到两枚硬币的概率,前提是给定我们已经观察到一种结果出现a次、另一种结果出现b次。
β \beta β 分布代表了所有可能的二项分布对观察结果的最高描述程度。
2. 将概率密度函数应用于我们的问题
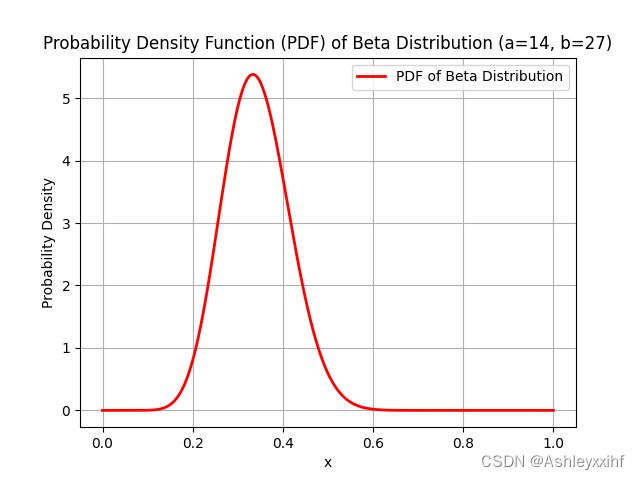
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
# 定义参数
a = 14
b = 27
# 生成 x 值的范围
x = np.linspace(0, 1, 1000)
# 计算 Beta 分布的概率密度函数(PDF)
pdf = beta.pdf(x, a, b)
# 绘制图形
plt.plot(x, pdf, 'r-', lw=2, label='PDF of Beta Distribution')
plt.title('Probability Density Function (PDF) of Beta Distribution (a=14, b=27)')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()
通过这个黑盒子赔钱的概率要比赢钱的概率大。虽然通过图5-3可以看出信念的分布,但我们还是希望能够准确地量化自己相信“黑盒子返回两枚硬币的概率小于0.5”的程度。要做到这一点,我们只需要懂一点微积分(和R语言)。
用积分量化连续分布
计算曲线下面积:积分
作者之前是不熟悉积分的,所以我们会从最基本的概念开始理解。依旧a=14; b=27, 我们想知道:吐出两枚硬币的可能性是 1 2 \frac {1}{2} 21 的概率是多少?
我们知道概率的基本规则是,所有概率的和必然等于1。但在连续分布里,每个单独的值都无穷小,这就意味着任何特定值的概率实际上都是0。
二项分布:想象一下,你把一块1千克重的巧克力(相当大!)平均分成了两份,那么每份就有 1 2 \frac {1}{2} 21 千克重。
连续分布:如果你把它平均分成了10份,那么每份将重 1 10 \frac {1}{10} 101千克。随着你将巧克力分成的份数越来越多,每一份就会变得越来越小,小到你甚至看不见它。当分成的份数无穷大时,每一份就会小得看不见,就好像消失了!
即使单独的每一份都消失了,我们仍然可以讨论一定范围内的情况。例如,即使将一块1千克重的巧克力分成了无限多块,我们仍然可以将其中一半块数的重量加起来。同样,当讨论连续分布中的概率时,我们也可以将某个范围内的值相加。但如果每个具体的值都接近于0,那么它们的和是不是仍然等于0呢?
积分
这就是微积分要解决的问题。在微积分中,有一种求无穷小值和的特殊方法,叫作积分(integral)。如果想知道黑盒子返回硬币的概率是否小于0.5(也就是值在0和0.5之间),那么我们可以这样求和:
∫ 0 0.5 f ( x ) d x \int_{0}^{0.5} f(x) \, dx ∫00.5f(x)dx
这里的∫只是一个拉伸后的S,意思是f(x)中所有矩形的面积之和。dx符号则提醒我们所谈论的是变量x很小的变化;d是表示这些矩形的一种数学方法。当然,在这个符号中只有一个变量x,所以我们不会混淆。而且,在本书中通常会删除dx(或变量中所使用的相应值),因为即使在示例中不写,我们也可以明白。
d i s t ( T ) = ∫ 0 T f ( t ) d t dist(T)= \int_{0}^{T} f(t) \, dt dist(T)=∫0Tf(t)dt
积分可以帮助我们把“某一时间的速度”,转化为函数即“某一段时间的跑步距离”。
度量变化率:导数
这里使用了类似于前面解释积分的方法:积分时把曲线下的区域分成越来越细的矩形,直到包含无数个细矩形,然后将它们的面积相加;只不过这里是把曲线分成无数个小线段。最终,我们得到了一个新的函数而不是单一的斜率m,来表示原始函数中每个点的变化率。这被称为导数(derivative).
d d x F ( x ) = f ( x ) \frac{d}{dx}F(x)=f(x) dxdF(x)=f(x)
F为f的原函数。
现在假设对函数f,我们想在10和50之间对其积分,也就是要计算:
∫ 10 50 f ( x ) d x = F ( 50 ) − F ( 10 ) \int_{10}^{50} f(x) \, dx=F(50)-F(10) ∫1050f(x)dx=F(50)−F(10)
积分和导数之间的关系被称为微积分基本定理(fundamental theorem of calculus)。这是一个相当神奇的工具,因为它允许用数学方法来解决积分问题,这往往要比求导数困难得多。
3. R语言实践
R语言中有一个名为dbeta()的函数,它就是beta分布的PDF。将它和integrate()函数一起使用就可以自动计算积分。
计算0-0.5之间的概率密度:
> integrate(function(p) dbeta(p,14,27),0,0.5)
结果:
0.9807613 with absolute error < 5.9e-06
之所以出现绝对误差(absolute error),是因为计算机不能完美地计算积分,而总会有一些误差。不过通常情况下误差很小,我们不用担心。R语言计算出的这个结果告诉我们,根据目前观察到的数据,从黑盒子中得到两枚硬币的真实概率小于0.5的概率高达0.98。这意味着往黑盒子里放更多的硬币不是好主意,因为你很有可能会输钱。
我们可以用收集到的数据去计算抽牌/抽奖时,是否应该去碰运气。
4. 小结
在本章中,我们学习了Beta分布,它与二项分布密切相关,其起作用的方式却大不相同。我们通过观察大量可能的二项分布对数据的解释程度建立了Beta分布。由于假设的数量无穷多,因此我们需要一个连续的概率分布来描述所有的假设。Beta分布让我们能够表示自己对所有可能结果的出现概率有多大信心。这使得我们能够对观察到的数据进行统计推理,其方式是通过确定将哪些概率分配给一个事件以及确定自己相信每个概率的程度,这就是表示概率范围的概率。
Beta分布与二项分布的主要区别在于,Beta分布是一个连续的概率分布。由于在分布中有无限多的值,因此我们不能像在离散概率分布中那样对结果进行求和,而是需要使用微积分对一定范围内的数值进行求和。幸运的是,我们可以使用R语言代替手动求解复杂的积分。