【Transformer】Transformer的简单了解:Positional Encoding、Self-attention、Batch 与 Layer Norm 等
自从2017年Transformer模型被提出以来,它已经从论文最初的机器翻译领域,转向语音,图像,视频等等方面的应用。最近的Segment Anything论文提出,阅读论文其中大量的transformer的在图像方面的应用。所以这里还是加紧记录下transformer相关内容。
- transformer初了解
- Positional Encoding(位置编码)
- Self-attention(自注意力机制)
- Batch & Layer Norm(批量归一化/层标准化)
- transformer的结构
- 补充:ResNet(残差网络)
一、Transformer的提出
在NLP中,RNN对文本的学习可以考虑词的先后顺序对预测的影响。
- 运行机制
- 在RNN当中,tokens是一个一个被喂给模型的。比如在a3的位置,模型要等a1和a2的信息都处理完成后,才可以生成a3。也是这样的机制,有了如下的特点和问题:
- 特点:
- 1 顺序处理:句子必须逐字处理
- 2 RNN指的是一个序列当前的输出与之前的输出也有关,具体的表现形式为网络会对前面的信息进行记忆。
记忆保存在网络的内部状态中,并应用于当前输出的计算中,即隐藏层之间的节点是有连接的,并且隐藏层的输入不仅包含输入层的输出还包含上一时刻隐藏层的输出- 3它采取线性序列结构不断从前往后收集输入信息
- 缺点:
- 1 无法支持长时间序列(容易梯度消失)
- RNN网络中,时间是串联关系,越远的隐藏层的输出 对当前隐藏层的输出的影响越小。
- 2 RNN网络对所有序列输入是平等对待,没有区分信息的重要性:有用、无用、辅助。
- 3 序列操作和最大路径长度的复杂度,随着序列长度的增加而增加。
后来提出RNN网络的升级版本, LSTM网络能够根据词的重要性有选择性的进行丢弃和记忆。
直到2017年,谷歌提出了transformer,当时主要应用于NLP领域的各个任务中。
其最大特点是抛弃了CNN和RNN,整个网络结构完全由attention机制组成。由于其出色的性能以及对下游任务的友好性,或者说对下游任务仅仅微调即可取得不错的效果,因此,在CV领域,不断有人尝试将transformer引入。比如典型的有目标检领域的dert和可变形dert,分类领域的vision transformer等。
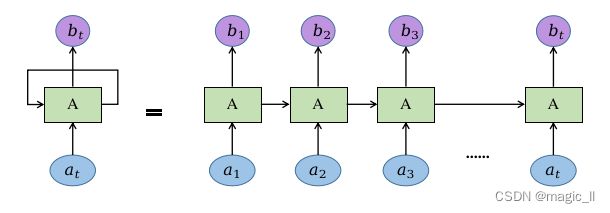
- 运行机制:如图,浅绿色方框为一个attention模型。

- 在每个位置,例如在a2处产生b2时,attention将会同时看过a1到a4的每个token。
- 每个token生成其对应的输出的过程是同时进行的,计算不需要等待。
- 特点:
- 可以直接计算每个词之间的相关性,不需要通过隐藏层传递
- 可以并行计算,可以充分利用GPU资源
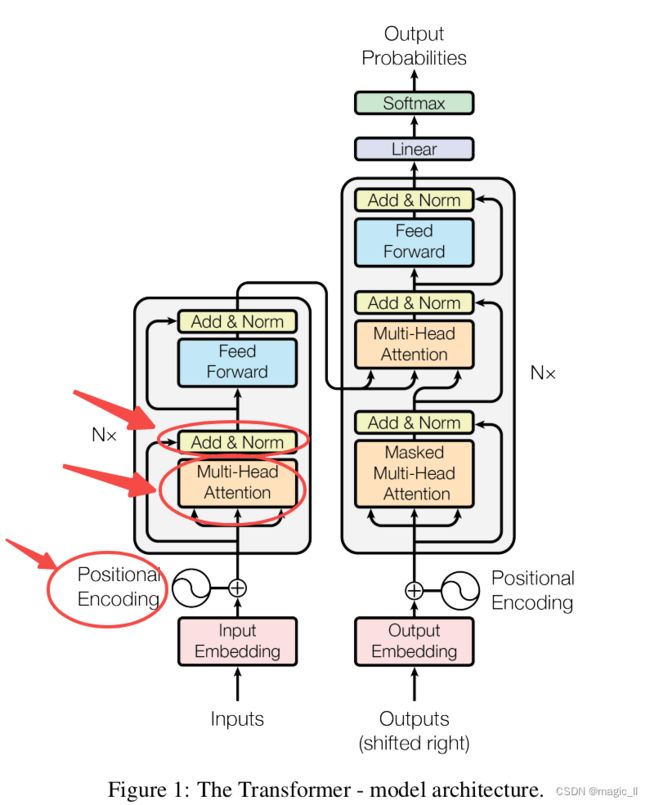
transformer论文中的一个重要的结构图:
接下来会记录的内容:
二、Positional Encoding(位置编码)
2.1 位置编码的必要性
positional_encoding的添加
在transformer中的encoder和decoder的输入层中,使用了Positional Encoding,使得输入包含了位置信息:
input = input_embedding+positional_encoding \text{input = input\_embedding+positional\_encoding} input = input_embedding+positional_encoding。
这里 input_embedding 为原本正常的输入的 token,是从单词长短转换成d_model维度;positional_encoding 表示词在文本序列的位置。
假设input_enbeddings 的维度为4,则实际的位置编码可如下所示:
positional_encoding的必要性
在原理上Transformer中的 self-attention 是无法隐式学到序列的位置信息的,不会区别输入的前后顺序,这样训练的结果对text中词组顺序的变化无感。比如:“小猫在小狗前面”和“小狗在小猫前面”是同意,显然这样是不行的。
为了可以处理序列问题,Transformer提出者的解决方案是使用位置编码(Position Encode/Embedding,PE),并且为了计算方便使用绝对位置编码,即序列中每个位置都有一个固定的位置向量。
2.2 位置编码的方法 /演变历程
我们想要一种位置表达方式,满足于:
(1)能用来表示一个token在序列中的绝对位置
(2)在序列长度不同的情况下,不同序列中token的相对位置/距离也要保持一致
(3)可以用来表示模型在训练过程中从来没有看到过的句子长度。
可以使用的位置编码形式
【用整型值】
最直接的想法:给第一个token标记1,给第二个token标记2…。但会存在问题:
- 不利于泛化:模型可能遇到比训练时所用的序列更长的序列
- 模型的位置无界,不利于收敛:随着序列的增加,位置值会越来越大,网络直接输入无界的数值无法得到很好的收敛。
【 用[0,1]范围的list】
为了解决整型值带来的问题,可以之间将值的范围限制在[0,1]之间。0代表第一个token,1代表最后一个token,n个token就用stride=1/(n-1)的list代表。
比如:共3个token对应位置信息为 [0,0.5,1];共4个token对应位置信息为 [0,0.33,0.69,1]。
依然存在问题:当序列长度不同时,token的相对距离是不一样的。长度的不一致会使得网络无法很好的获取到当前text中的位置信息【用二进制向量】
可以选择将位置信息添加到input embedding上。比起使用单一的值,使用一个positional encoding来表示,然后与input embedding相加,这样添加的信息更平稳些。 能够相加说明两者需要相同的维度,如此二进制编码则被考虑到。【使用正余弦函数】
在transformer中,位置编码选择了正余弦函数。实现了如下功能:
- 每个token的向量唯一
- 位置向量的值是有界的,且在连续的空间中。这样模型在处理位置编码向量时更容易泛化,也就是能够更好的处理长度和训练数据分布不一致的序列。
有公式如下:
P E ( p o s , 2 i ) = sin ( p o s 1000 0 2 i / d m o d e l ) P E ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i / d m o d e l ) PE(pos,2i)=\sin(\frac{pos}{10000^{2i/d_{model}}}) \\ PE(pos,2i+1)=\cos(\frac{pos}{10000^{2i/d_{model}}}) PE(pos,2i)=sin(100002i/dmodelpos)PE(pos,2i+1)=cos(100002i/dmodelpos)
- PE:位置编码。维度为(n, d m o d e l d_{model} dmodel),其中n为词的个数, d m o d e l d_{model} dmodel为位置编码的维度
- pos:当前词在n个词中的序列位置
- i:【2i 和 2i+1】 表示每个词在维度为 d m o d e l d_{model} dmodel的编码的第i个位置的数值, i = 0 , 1 , 2 , . . . , d m o d e l 2 − 1 i=0,1,2,...,\frac{d_{model}}{2}-1 i=0,1,2,...,2dmodel−1
2.3 正余弦函数
2.3.1 函数数值的变化
对于上面的公式,个人直接看并不能感受到其变化情况,所以这里做一个曲线的绘制。认知上面公式,我们先了解sin的曲线变化情况 P E ( p o s , i ) = sin ( p o s 1000 0 i / d m o d e l ) i = 0 , 1 , 2 , . . . , d m o d e l − 1 PE(pos,i)=\sin(\frac{pos}{10000^{i/d_{model}}})\,\,\,\,\,\,i=0,1,2,...,d_{model}-1 PE(pos,i)=sin(10000i/dmodelpos)i=0,1,2,...,dmodel−1
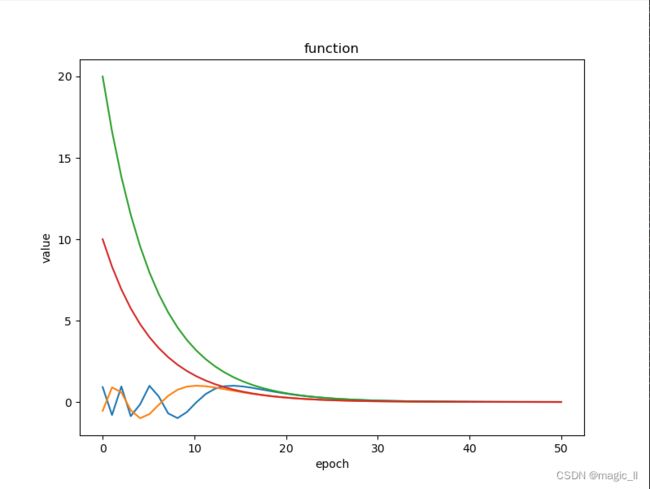
假设通过正余弦位置编码成维度为50的向量,当pos分别为10、20时,则有以下曲线
- 绿色曲线: y = 20 1000 0 i / 50 y=\frac{20}{10000^{i/50}} y=10000i/5020,也就是pos=20, d m o d e l d_{model} dmodel=50
- 红色曲线: y = 10 1000 0 i / 50 y=\frac{10}{10000^{i/50}} y=10000i/5010,也就是pos=10, d m o d e l d_{model} dmodel=50
- 蓝色曲线: y = sin ( 20 1000 0 i / 50 ) y=\sin(\frac{20}{10000^{i/50}}) y=sin(10000i/5020)
- 橙色曲线: y = sin ( 10 1000 0 i / 50 ) y=\sin(\frac{10}{10000^{i/50}}) y=sin(10000i/5010)
可以看到,对于 y = p o s 1000 0 i / 50 y=\frac{pos}{10000^{i/50}} y=10000i/50pos,当 i = 0 i=0 i=0时, y ≈ p o s y\approx pos y≈pos,当 i = 49 i=49 i=49, y ≈ 0 y\approx 0 y≈0,且在前期快速下降;对应的 y = sin ( p o s 1000 0 i / 50 ) y=\sin(\frac{pos}{10000^{i/50}}) y=sin(10000i/50pos)会在前期快速震荡,后期趋于稳定。
对于pos,越大时候, y = sin ( 10 1000 0 i / 50 ) y=\sin(\frac{10}{10000^{i/50}}) y=sin(10000i/5010)在初期震荡频率越高,越靠后越趋于稳定。
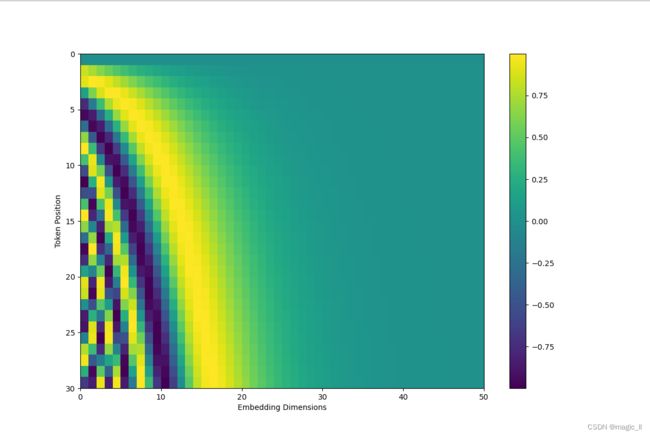
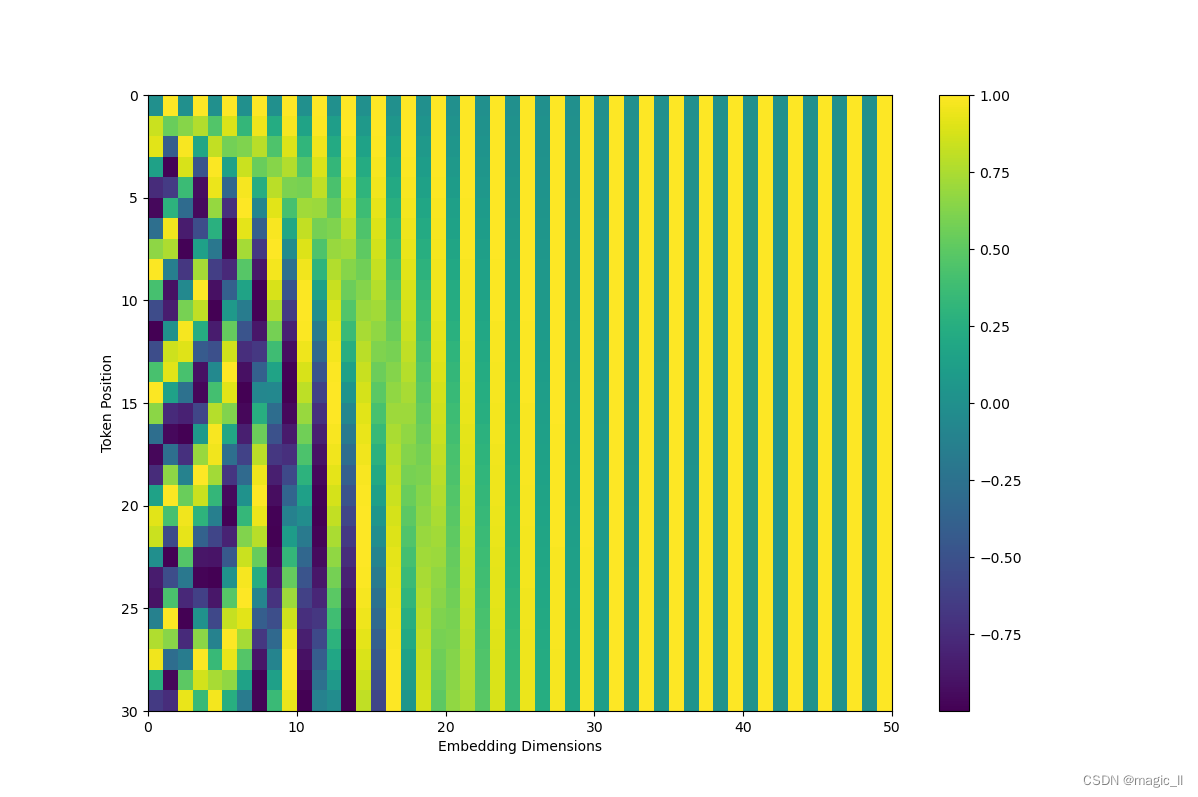
当有词数量为30时,将其每个词的位置编码绘制成图如下
当我们对位置编码的奇数位置使用cos,偶数位置使用sin,就有了正余弦编码函数 P E ( p o s , 2 i ) = sin ( p o s 1000 0 2 i / d m o d e l ) P E ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i / d m o d e l ) PE(pos,2i)=\sin(\frac{pos}{10000^{2i/d_{model}}}) \\ PE(pos,2i+1)=\cos(\frac{pos}{10000^{2i/d_{model}}}) PE(pos,2i)=sin(100002i/dmodelpos)PE(pos,2i+1)=cos(100002i/dmodelpos)类似的有:
2.3.2 正余弦函数的性质
正余弦编码具有如下性质:
- 1 两个位置编码的点积 (dot product) 仅取决于偏移量k,即 两个位置编码的点积可以反映出位置间的距离
- 2 位置编码的点积是无向的,即 P E t T ∗ P E t + k = P E t + k T ∗ P E t = ∑ j = 0 d 2 − 1 cos ( w j k ) PE^{T}_{t}*PE_{t+k}=PE^{T}_{t+k}* PE_{t}=\sum^{\frac{d}{2}-1}_{j=0}\cos(w_jk) PEtT∗PEt+k=PEt+kT∗PEt=∑j=02d−1cos(wjk)。
简单证明:
P E t + k = ( s i n ( w 0 ( t + k ) ) c o s ( w 0 ( t + k ) ) . . . s i n ( w d 2 − 1 ( t + k ) ) c o s ( w d 2 − 1 ( t + k ) ) ) P E t + k = ( s i n ( w 0 t ) ) c o s ( w 0 t ) . . . s i n ( w d 2 − 1 t ) c o s ( w d 2 − 1 t ) ) P E t T P E t + k = P E t + k T P E t = ∑ j = 0 d 2 − 1 [ sin ( w j t ) sin ( w j ( t + k ) ) + cos ( w j t ) cos ( w j ( t + k ) ) ] = ∑ j = 0 d 2 − 1 cos ( w j ( t − ( t + k ) ) ) = ∑ j = 0 d 2 − 1 cos ( w j k ) \begin{aligned} PE_{t+k}&=\left( \begin{matrix} sin(w_0(t+k) )\\ cos(w_0(t+k) )\\ ... \\ sin(w_{\frac{d}{2}-1}(t+k))\\ cos(w_{\frac{d}{2}-1}(t+k)) \\ \end{matrix} \right) \\ PE_{t+k}&=\left( \begin{matrix} sin(w_0t))\\ cos(w_0t )\\ ... \\ sin(w_{\frac{d}{2}-1}t)\\ cos(w_{\frac{d}{2}-1}t) \\ \end{matrix} \right) \\ PE^{T}_{t}PE_{t+k}&=PE^{T}_{t+k} PE_{t}\\ &=\sum^{\frac{d}{2}-1}_{j=0}[\sin(w_jt)\sin(w_j(t+k))+\cos(w_jt)\cos(w_j(t+k))] \\ &=\sum^{\frac{d}{2}-1}_{j=0}\cos(w_j(t-(t+k))) \\ &=\sum^{\frac{d}{2}-1}_{j=0}\cos(w_jk) \end{aligned} PEt+kPEt+kPEtTPEt+k= sin(w0(t+k))cos(w0(t+k))...sin(w2d−1(t+k))cos(w2d−1(t+k)) = sin(w0t))cos(w0t)...sin(w2d−1t)cos(w2d−1t) =PEt+kTPEt=j=0∑2d−1[sin(wjt)sin(wj(t+k))+cos(wjt)cos(wj(t+k))]=j=0∑2d−1cos(wj(t−(t+k)))=j=0∑2d−1cos(wjk)
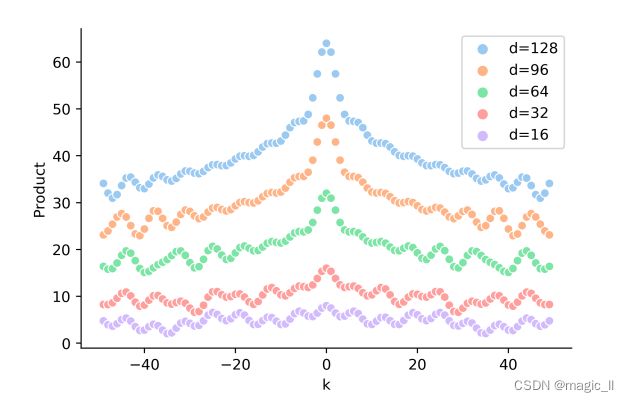
以某个位置编码 P E t PE_t PEt为基准,去计算它左右距离k的位置编码的点积,可得到如下图。可以发现,当距离k越大时内越小,反之越大。且点积能表示距离,无法表示方向。
2.3.3 正余弦编码在transformer中
对于一个句子中,我们能够很容易的知道词的位置信息,比如“小猫 在 小狗 前面 趴着”:
1) 绝对位置信息:"小猫"是在第一个位置,"在"是在第二个位置,"小狗"是在第三个位置…
2) 相对位置信息:"小狗"在"小猫"后面2位,"趴着"在"小猫"后面4位…
在输入上添加了位置编码,对于self-attention模块我们希望网络在理解绝对位置信息的同时,也能理解词与词之间的相对位置信息,那么这里探究下正余弦位置编码包含相对位置信息吗?通过正余弦函数的性质,我们直到点积能够反映距离但无法反映方向,那经过self-attention模块后,位置编码信息会发生怎样的情况呢?
- 在self-attention模块中,
W q 、 W k W_q、W_k Wq、Wk分别为multi-head attention给每个head的query和key参数(这部分后续会讲)
E x i 、 E x j E_{xi}、E_{xj} Exi、Exj是 x j xj xj和 x i xi xi的词嵌入
U i 、 U j U_i、U_j Ui、Uj是第i个位置和第j个位置的位置向量
可得表达式为:
A i , i a b s = ( W q ( E x i + U i ) ) T ( W w ( E x j + U j ) ) = E x i T W q T W k E x j + E x i T W q T W k U j + U i T W q T W k E x j + U i T W q T W k U j \begin{aligned} A^{abs}_{i,i}&=(W_q(E_{x_i}+U_i))^T(W_w(E_{x_j}+U_j))\\ &=E^T_{x_i}W^{T}_{q}W_kE_{x_j} + E^T_{x_i}W^{T}_{q}W_kU_{j}+ U^T_iW^{T}_{q}W_kE_{x_j} + U^T_iW^{T}_{q}W_kU_{j} \end{aligned} Ai,iabs=(Wq(Exi+Ui))T(Ww(Exj+Uj))=ExiTWqTWkExj+ExiTWqTWkUj+UiTWqTWkExj+UiTWqTWkUj
其中,第一项中没有位置编码信息,第二三项只包含一个位置编码信息,所以前三者都不包含相对位置信息。第四项同时包含两个位置编码,是最有可能包含相对位置信息。
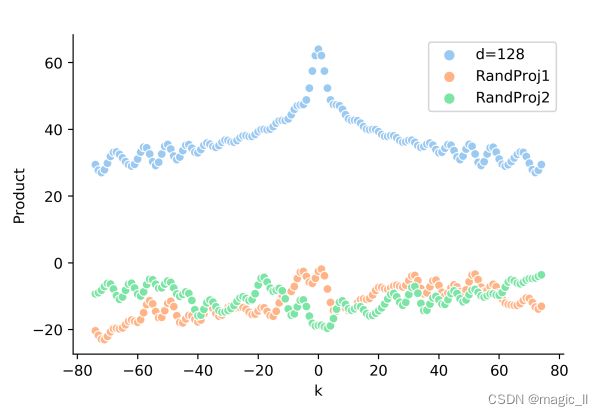
对于第四项, U i T W q T W k U j U^T_iW^{T}_{q}W_kU_{j} UiTWqTWkUj,随机初始化 W q 、 W k W_q、W_k Wq、Wk,然后将 U i T U j U_i^TU_j UiTUj, U i T W q T U j U_i^TW^{T}_{q}U_j UiTWqTUj, U i T W k U j U_i^TW_{k}U_j UiTWkUj这三个点积进行比较的下图。可以发现,中间随机的矩阵会破坏点积的相对位置信息,也就是位置编码进入attention中后,相对位置信息会丢失。
后续:
即然相对位置信息在经过attention模块中丢失了,那就在attention模块计算后将相对位置信息添加回来。Transformer改进之相对位置编码这个链接的作者介绍了后续三篇针对该问题改进的论文,这里只做记录链接,不做过多讨论
三、自注意力机制
Attention机制:它使得模型在学会将注意力集中在输入序列的特定部分。
硬性注意力机制:关注某一个输入向量。
软性注意力机制:所有输入向量在注意力分布下的期望。3.1 硬性注意力(Hard Attention)
有两种实现方式:
- 选取高概率的一个输入向量 a t t ( X , q ) = x n ^ att(X,q)=x_{\hat{n}} att(X,q)=xn^,其中 n ^ = arg max n = 1 N α n \hat{n}=\argmax^N_{n=1}\alpha_n n^=argmaxn=1Nαn为概率最大的输入向量的下标
- 通过在注意力分布上 随机采样的方式(投掷子)
缺点:
- 最终的损失函数与注意力分布之间的函数关系不可导,不能反向传播,需要使用强化学习训练。
3.2 软性注意力机制
计算方式:1 在所有输入信息上计算注意力分布;2 根据注意力分布计算输入信息的加权平均
计算注意力分布
用 X = [ x 1 , x 2 , . . . , x n ] ∈ R X=[x_1, x_2,...,x_n]\in R X=[x1,x2,...,xn]∈R 表示N组输入信息,其中 x n ∈ R , n ∈ [ 1 , N ] x_n ∈R, n ∈ [1, N] xn∈R,n∈[1,N]表示一组输入信息。
加权的通用表达式 X ′ = α 1 x 1 + α 2 x 2 + . . . + α n x n X^{'}=\alpha_1x_1+\alpha_2x_2+...+\alpha_nx_n X′=α1x1+α2x2+...+αnxn,这里注意力分布就是 α = [ α i , . . α n ] \alpha=[\alpha_i,..\alpha_n] α=[αi,..αn],那我们的重点就是计算这个注意力分布 α \alpha α
- 引入一个和任务相关的查询向量 q,然后用一个打分函数 S ( x n , q ) S(x_n,q) S(xn,q) 来计算每个输入向量 x n x_n xn 和查询向量之间的相关性(相似度) s n s_n sn , s n = S ( x n , q ) s_n=S(x_n,q) sn=S(xn,q):
- 加性模型: S ( x , q ) = v T tanh ( W x + U q ) S(x,q)=v^T\tanh(Wx+Uq) S(x,q)=vTtanh(Wx+Uq)
- 点积模型: S ( x , q ) = x T q S(x,q)=x^Tq S(x,q)=xTq
- 缩放点积模型: S ( x , q ) = x T q D S(x,q)=\frac{x^Tq}{\sqrt{D}} S(x,q)=DxTq
当输入向量的维度比较高的时候点积模型容易方差太大,从而导致Softmax函数梯度较小,使用缩放点积模型来解决这个问题;双线性模型是一种泛化的点积模型。也是transformer采用的方式- 双线性模型: S ( x , q ) = x T W q S(x,q)=x^TWq S(x,q)=xTWq
其中 W、U、v为可学习的参数,D为输入向量的维度- 我们将相似度作为权重,来提取每个 x n x_n xn的信息。这样就需要对该权重进行归一化,这里使用 softmax,则最终的权重为 α n = s o f t m a x ( S ( x n , q ) ) = exp ( S ( x n , q ) ) ∑ j = 1 N exp ( S ( x j , q ) ) \alpha_n=softmax(S(x_n,q))=\frac{\exp(S(x_n,q))}{\sum^N_{j=1}\exp(S(x_j,q))} αn=softmax(S(xn,q))=∑j=1Nexp(S(xj,q))exp(S(xn,q))
加权平均
前面我们得到注意力分布 α n \alpha_n αn:对给定任务 进行相关查询 q 时, α n \alpha_n αn为 第 n 个输入向量受关注的程度。
然后就可以根据注意力分布,获取对应的关注信息,然后进行加权得到,对于查询Q在整个输入X中提取的信息。
a t t ( X , q ) = ∑ n = 1 N α n x n = ∑ n = 1 N s o f t m a x ( S ( x n , q ) ) x n = ∑ n = 1 N exp ( S ( x n , q ) ) ∑ j = 1 N exp ( S ( x j , q ) ) x n (1) \begin{aligned} att(X,q) &= \sum^N_{n=1}\alpha_nx_n \\ &= \sum^N_{n=1} softmax(S(x_n,q))x_n \\ &=\sum^N_{n=1} \frac{\exp(S(x_n,q))}{\sum^N_{j=1}\exp(S(x_j,q))}x_n \end{aligned} \tag{1} att(X,q)=n=1∑Nαnxn=n=1∑Nsoftmax(S(xn,q))xn=n=1∑N∑j=1Nexp(S(xj,q))exp(S(xn,q))xn(1)
3.3 键值对注意力(key-calue Attention)
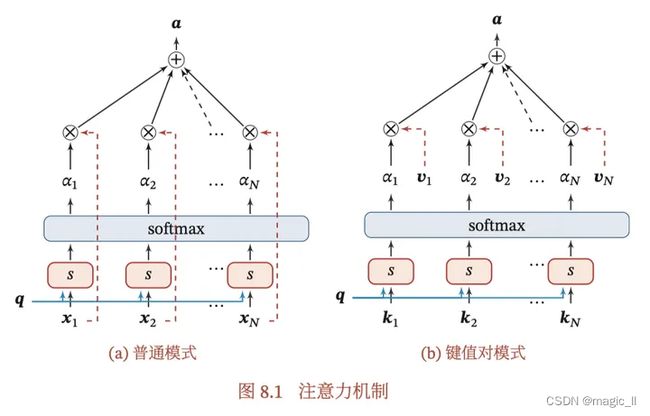
是软注意力机制的延伸体。键 用来计算注意力分布 attention(X,q),值 用来计算聚合信息。
用 ( K , V ) = [ ( k 1 , v 1 ) , . . . , ( k N , v n ) ] (K,V)=[(k_1,v_1),...,(k_N,v_n)] (K,V)=[(k1,v1),...,(kN,vn)] 表示N组输入信息,给定任务相关的查询向量q时,注意力函数为
a t t ( ( K , V ) , q ) = ∑ n = 1 N α n v n = ∑ n = 1 N s o f t m a x ( S ( k n , q ) ) v n = ∑ n = 1 N exp ( S ( k n , q ) ) ∑ j = 1 N exp ( S ( k j , q ) ) v n (2) \begin{aligned} att((K,V),q) &= \sum^N_{n=1}\alpha_nv_n \\ &= \sum^N_{n=1} softmax(S(k_n,q))v_n \\ &=\sum^N_{n=1} \frac{\exp(S(k_n,q))}{\sum^N_{j=1}\exp(S(k_j,q))}v_n \end{aligned} \tag{2} att((K,V),q)=n=1∑Nαnvn=n=1∑Nsoftmax(S(kn,q))vn=n=1∑N∑j=1Nexp(S(kj,q))exp(S(kn,q))vn(2)对比公式(1)(2),可以看到键值对注意力机制中,K代替了原本注意力机制中 计算注意力分布阶段的X;V 代替了原本注意力机制中 加权阶段的X。 我们将其画成图进行对比如下:
3.3 transformer中的自注意力机制
- 循环神经网络由于信息传递的容量以及梯度消失问题,实际上也只能建立短距离依赖关系。
- 为了建立长距离的依赖关系,可以增加网络的层数或者使用全连接网络。但全连接网络无法处理边长的出入序列。另外,不同的输入长度,其连接权重的大小也是不同的。
transformer提出了的自注意力模型,可以输入不同的长度数据。
自注意模型的结构经常采用QKV (Query-Key-Value)模式。对于已有的特征矩阵X,要通过 s e l f _ a t t e n t i o n ( ( K , V ) , Q ) self\_attention((K,V),Q) self_attention((K,V),Q)提取特征H,其中 QKV 皆来自于X。计算过程如下图所示:
假设输入序列 X = [ x 1 , . . . , x n ] ∈ R d m o d e l ∗ N X=[x_1,...,x_n]\in R^{d_{model}*N} X=[x1,...,xn]∈Rdmodel∗N,输出序列为 H = [ h 1 , . . . , h N ] ∈ R d v ∗ N H=[h_1,...,h_N]\in R^{d_v*N} H=[h1,...,hN]∈Rdv∗N,则计算过程如下:
- 通过 X 获取 QKV
对于每个输入,首先将其映射到三个不同的空间,得到三个向量:查询向量 q i ∈ R d k q_i\in R^{d_k} qi∈Rdk、键向量 k i ∈ R d k k_i\in R^{d_k} ki∈Rdk、值向量 v i ∈ R d v v_i \in R^{d_v} vi∈Rdv。生成方法为当前词的词嵌入表示分别乘以三个矩阵,这些矩阵在训练过程中需要学习。(注意:不是每个词向量独享3个matrix,而是所有输入共享3个转换矩阵)
Q = W q X ∈ R d k ∗ N K = W k X ∈ R d k ∗ N V = W v X ∈ R d v ∗ N Q=W_qX\in R^{d_k*N} \\ K=W_kX\in R^{d_k*N} \\ V=W_vX\in R^{d_v*N} Q=WqX∈Rdk∗NK=WkX∈Rdk∗NV=WvX∈Rdv∗N其中, W q ∈ R d k ∗ d m o d e l W_q\in R^{d_k*d_{model}} Wq∈Rdk∗dmodel, W k ∈ R d k ∗ d m o d e l W_k\in R^{d_k*d_{model}} Wk∈Rdk∗dmodel, W v ∈ R d v ∗ d m o d e l W_v\in R^{d_v*d_{model}} Wv∈Rdv∗dmodel 分别为现行映射的参数矩阵
Q = [ q 1 , . . . , q N ] Q=[q_1,...,q_N] Q=[q1,...,qN], K = [ k 1 , . . . , k N ] K=[k_1,...,k_N] K=[k1,...,kN], V = [ v 1 , . . . , v N ] V=[v_1,...,v_N] V=[v1,...,vN],分别为查询向量、键向量、值向量构成的矩阵。
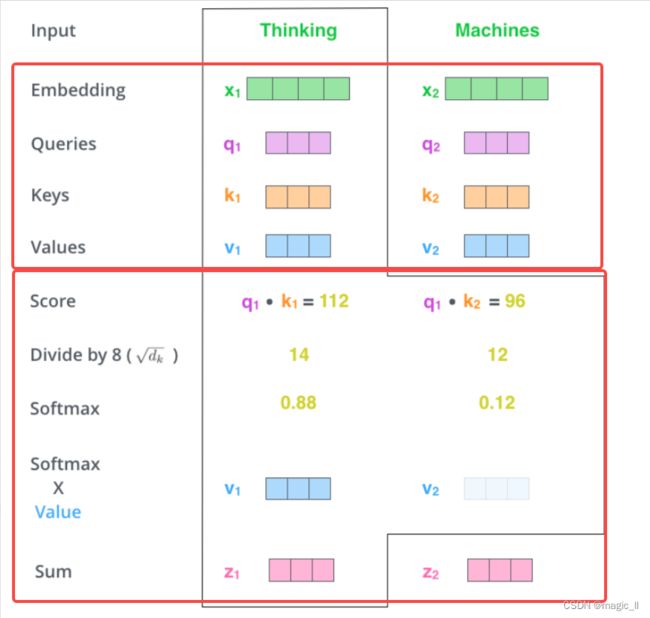
- 利用键值对注意力机制(公式(2)),对每个查询向量 q n q_n qn,计算对应的输出向量 h n h_n hn。 h n = a t t ( ( K , V ) , q n ) = ∑ j = 1 N α n j v j = ∑ j = 1 N s o f t m a x ( S ( k j , q n ) ) v j (2) \begin{aligned} h_n&=att((K,V),q_n) \\ &= \sum^N_{j=1}\alpha_{nj}v_j \\ &= \sum^N_{j=1} softmax(S(k_j,q_n))v_j \\ \end{aligned} \tag{2} hn=att((K,V),qn)=j=1∑Nαnjvj=j=1∑Nsoftmax(S(kj,qn))vj(2)其中, n , j ∈ [ 1 , N ] n,j\in [1,N] n,j∈[1,N]为输出和输入向量序列的位置, α n \alpha_n αn表示第n个输出关注到第 j 个输入的权重。
如果使用缩放点积作为注意力打分函数,则输出矩阵可以简写为 H = s o f t m a x ( K T Q D k ) V H=softmax(\frac{K^TQ}{\sqrt{D_k}})V H=softmax(DkKTQ)V
在transformer论文中,自注意机制还有额外的两个处理:mask的使用、多头的使用- 添加mask
矩阵可以简写为 H = s o f t m a x ( K T Q D k × m a s k ) V H=softmax(\frac{K^TQ}{\sqrt{D_k}}×mask)V H=softmax(DkKTQ×mask)V
- multi-headed的机制
- 在CNN中:卷积层具体的参数为 k ∗ k ∗ C i n ∗ C o u t k*k*C_{in}*C_{out} k∗k∗Cin∗Cout,每一个 C o u t C_{out} Cout 关注和转换一种特征信息。在transformer中等同的理解,one-head的self-attention相当于使用一个 k ∗ k ∗ C i n k*k*C_{in} k∗k∗Cin,multi-head 相当于 C o u t C_{out} Cout 个 k ∗ k ∗ C i n k*k*C_{in} k∗k∗Cin。
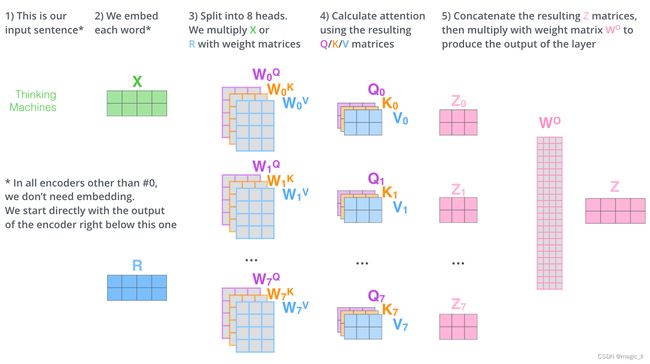
- 操作过程:设头的数量为 num \text{num} num 。(1)训练 n u m num num 个 W q 、 W k 、 W v W^q、W^k、W^v Wq、Wk、Wv 个矩阵, 用于生成 num \text{num} num 个 Q/K/V,然后计算 num \text{num} num 个H。(2) 将 num \text{num} num 个H 进行concat后,使用 W o W^o Wo整合下信息,得到最终的H。
- QKV的shape:在transformer的工作中,设置了 num = 8 \text{num}=8 num=8,对每一个模型都使用了 d k = d v = d m o d e l / num = 64 d_k=d_v=d_{model}/\text{num}=64 dk=dv=dmodel/num=64。这种设置与单头的 d k = d v = d m o d e l = 512 d_k=d_v=d_{model}=512 dk=dv=dmodel=512时的总计算量是相似的。
- 公式为: MultiHead(Q,K,V) = Concat(Attention ( Q W i Q , K W i K , V W i V ) , . . . ) W O \text{MultiHead(Q,K,V)}=\text{Concat(Attention}(QW^Q_i,KW^K_i,VW^V_i),...) W^O MultiHead(Q,K,V)=Concat(Attention(QWiQ,KWiK,VWiV),...)WO
四、Batch Normalization 与 Layer Normalization
4.1 Batch Normalization
4.1.1 Internal Covariate Shift 与 BN的提出
1【Internal Covariate Shift 】
Batch Normalization(简称BN)在2015年被提出,主要用于解决深度学习中的Internal Covariate Shift 的问题
- Covariate shift:若模型输入层数据发生变化,则模型在该批变化数据上的表现将有所波动,输入层分布的变化成为 Covariate Shift
- Internal Covariate Shift(ICS):在深度学习中,第L+1层的输入,也可以随着第L层参数的变动而引起分布的变动。这样每一层在训练时,都要去适应这样的分布变化,是的训练变得困难。这种层间输入分布变动的情况,就是Internal Covariate Shift。
对应公式有:
Z [ L ] = W [ L ] ∗ A [ L − 1 ] + b [ L ] A [ L ] = g [ L ] ( Z [ L ] ) Z^{[L]} = W^{[L]}*A^{[L-1]}+b^[L] \\ A^{[L]}=g^{[L]}(Z^{[L]}) Z[L]=W[L]∗A[L−1]+b[L]A[L]=g[L](Z[L])第一行是线性变化层;第二行是非线性变化层,也是激活函数层。
随着梯度下降, W [ L ] W^{[L]} W[L]和 b [ L ] b^{[L]} b[L] 都会被更新,则 Z [ L ] Z^{[L]} Z[L] 的分布会改变,然后影响L+1层的输出 A [ L ] A^{[L]} A[L] 的分布2【ICS带来的问题】
3【解决ICS的常规方法】
ICS产生的原因是由于参数更新带来的网络中每一层输入值分布的改变,并且随着网络层数的加深而变得更加严重,因此我们可以通过固定每一层网络输入值的分布来对减缓ICS问题。
网络设置上
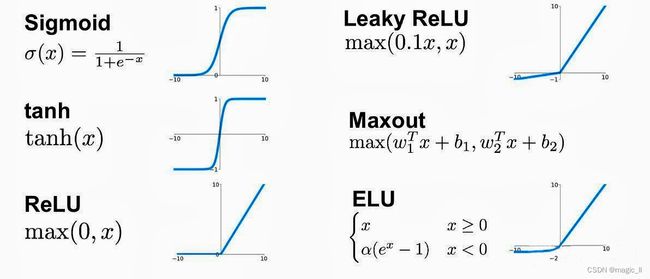
- 采用非饱和激活函数
- 采用更小的学习率
- 更加细致的参数初始化方法
数据白化
白化(Whitening)是机器学习里面常用的一种规范化数据分布的方法,主要是PCA白化与ZCA白化。白化是对输入数据分布进行线性变换,进而达到以下两个目的
- 使得输入的特征具有相同的均值和方差。其中PCA白化保证了所有特征分布均值为0,方差为1;而ZCA白化则保证了所有特征分布均值为0,方差相同
- 去除特征之间的相关性
问题:
- 白化过程计算成本太高,并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作;
- 白化过程由于改变了网络每一层的分布,因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
Batch Normalization
- 能够简化计算过程
- 经过规范化处理后 让数据尽可能保留原始的表达能力
4.1.2 Batch Normalization在训练时
BN是在mini-batch对的基础上进行计算的。先摆公式,在讲原理
Z [ l ] = W [ l ] A [ l − 1 ] + b [ l ] μ = 1 m ∑ i = 1 m Z [ l ] ( i ) σ 2 = 1 m ∑ i = 1 m ( Z [ l ] ( i ) − μ ) 2 Z ~ l = γ ∗ Z [ l ] − μ σ 2 + ϵ + β A [ l ] = g [ l ] ( Z ~ [ l ] ) \begin{aligned} Z^{[l]}&=W^{[l]}A^{[l-1]}+b^{[l]} \\ \mu &= \frac{1}{m}\sum ^{m}_{i=1}Z^{[l](i)} \\ \sigma ^{2}&=\frac{1}{m}\sum^{m}_{i=1}(Z^{[l](i)}-\mu)^2 \\ \widetilde{Z}^{l}&=\gamma*\frac{Z^{[l]-\mu}}{\sqrt{\sigma^2+\epsilon }}+\beta \\ A^{[l]}&=g^{[l]}(\widetilde{Z}^{[l]}) \end{aligned} Z[l]μσ2Z lA[l]=W[l]A[l−1]+b[l]=m1i=1∑mZ[l](i)=m1i=1∑m(Z[l](i)−μ)2=γ∗σ2+ϵZ[l]−μ+β=g[l](Z [l])
- 第一行:第 l l l 层的输出特征矩阵的计算
- 第二三行:对输出矩阵进行归一化。
针对 卷积输出特征的channel通道,计算其均值方差 μ \mu μ、 σ \sigma σ(非学习参数);用于后面的减均值除方差。通过这种变换,完成了第一个任务:使用更简的方式对数据规范化,使得第 l l l 层的输入每个特征的分布均值为0,方差为1。
注意均值方差的计算是针对channel通道的。比如输出的维度为 (N,H,M,C),那么计算的 μ \mu μ、 σ \sigma σ 的维度为(1,1,1,C)- 第四行:引入两个可学习参数 γ \gamma γ、 β \beta β,恢复数据本身的表达能力
γ \gamma γ、 β \beta β为可学习的、维度为C的向量。特别的当 γ 2 = σ 2 \gamma^2=\sigma^2 γ2=σ2、 β = μ \beta=\mu β=μ 时,可以实现等价变换,并保留了原始特征的分布信息- 第五行:BN的输出送入到激活层
4.1.3 Batch Normalization在测试时
已知训练时的BN在每一层时, μ \mu μ 和 σ \sigma σ 基于当前batch中的数据。当测试时,batch为1 或者很小,此时少量或单个数据计算的 μ \mu μ、 σ \sigma σ一定是有偏差的,测试的计算应当如何?
- 使用训练集中的均值和方差做测试集中的均值和方差的无偏估计
保留训练模型中 每一组batch的数据在每一层的 μ b a t c h \mu_{batch} μbatch、 σ b a t c h 2 \sigma^2_{batch} σbatch2,如此可得到测试数据均值和方差的无偏估计:
μ t e s t = E ( μ b a t c h ) σ t e s t 2 = m m − 1 E ( σ t e s t 2 ) B N ( X t e s t ) = γ X t e s t − μ t e s t σ t e s t 2 + β \begin{aligned} \mu_{test} &= \mathbb{E}(\mu_{batch}) \\ \sigma^2_{test} &= \frac{m}{m-1}\mathbb{E}(\sigma^2_{test})\\ BN(X_{test}) &=\gamma \frac{X_{test}-\mu_{test}}{\sqrt{\sigma^2_{test}}}+\beta \end{aligned} μtestσtest2BN(Xtest)=E(μbatch)=m−1mE(σtest2)=γσtest2Xtest−μtest+β 其中m 表示batch_size。
缺点:需要消耗较大的存储空间,用来保存训练过程中所有的均值和方差。- Momentum:移动平均法
移动平均法其实比较常见。在这里具体的为:设 μ t \mu_t μt 为当前步骤计算的均值, μ ^ \hat{\mu} μ^为上一步训练时累计求得的均值,则有 μ ^ = p ∗ μ + ( 1 − p ) μ t \hat{\mu}=p*\mu+(1-p)\mu_t μ^=p∗μ+(1−p)μt其中 p 为momentum超参,表示模型在多大程度上依赖与过去的均值和方差。
同理,对于方差 σ ^ \hat{\sigma} σ^的计算公式有 σ 2 ^ = p ∗ σ 2 + ( 1 − p ) σ t 2 \hat{\sigma^2}=p*\sigma^2+(1-p)\sigma^2_t σ2^=p∗σ2+(1−p)σt2
优势:
1)节省了存储空间,无需保存所有的均值和方差,继续更新 滑动均值和滑动方差
2)方便在训练模型阶段监督模型的测试效果。一般的,在训练过程中,会使用验证集对模型训练的效果进行追踪。使用移动平均法,无需在模型训练结束后再对统计参数做无偏估计,可直接使用滑动均值滑动方差,对验证集进行模型评估。4.1.4 Batch Normalization 优势
- 加速模型学习速度:BN使得网络每层输入数据分布相对稳定,且输出在一定范围内。
- 缓解梯度消失:BN允许网络使用饱和型激活函数(sigmoid、tanh等)
- 简化调参过程:使用BN可以设置更大的学习率,可以不用谨慎调整模型初始化参数
- 具有一定正则性:实验发现,BN可以代替dropout,对网络起到正则效果
4.1.5 后来
在MIT的Santurkar How Does Batch Normalization Help Optimization?指出:
- ICS问题并没有使模型的表现更差
- BN对解决ICS问题的能力是有限的,起作用的原因是它让optimization 更平滑
在这之后也有其他论文对于这观点进行了不同论证与试验。
但目前而言,在图像上的模型,BN的使用依然是基本操作,BN的增加的确会简化我们的训练。
4.2 Layer Normalization
在RNN中,文本数据存在长短不一的问题。比如文本1:“天气/预报/今天/下大雨”,文本2:“小明/正在/吃饭”,这两个文本的词的数量是不一致,也就是长短不一的问题。
在图像中对应的问题是什么呢?是:训练时输入的图片长宽不一(对应文本长短不一),这样是无法在同一个batch中有效的进行BN操作的。当然图片是可以进行缩放的,使得同一个batch的图片的尺寸保持一致进而使用BN。但文本是不能进行缩放的。如果强行对文本进行BN,会有问题:
- 文本中后侧位置没有足够的batch_size的数据,前段数据可以正常的累计 μ \mu μ、 σ 2 \sigma^2 σ2,后段计算出来的 μ \mu μ、 σ 2 \sigma^2 σ2会产生偏差的。
- 当测试集中出现比训练集中更长的数据,多出去的部分是没有对应的 μ \mu μ、 σ 2 \sigma^2 σ2,对预测带来了极大的问题。
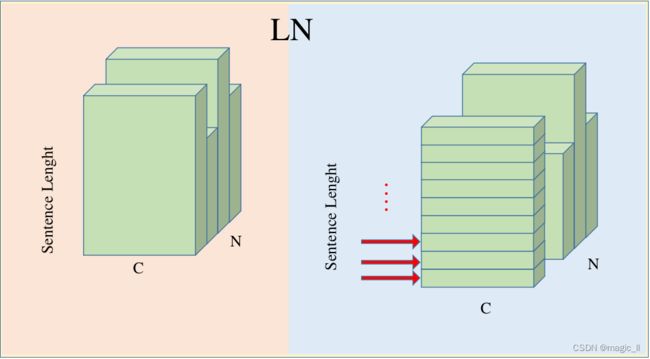
针对文本任务,Ba et al. 2016 提出在RNN上使用Layer Normalization(以下简称LN)的方法。接下来对比下两者的差异(以图片举例):
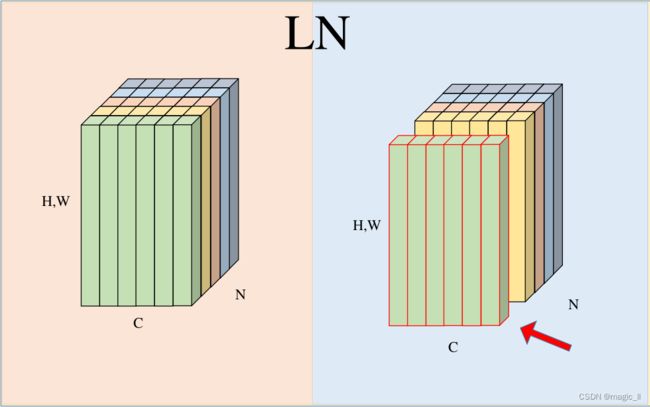
假设输入为(N,H,W,C),如下图左侧,一个颜色表示一个完整的数据(H,W,C);高度上表示为 H*W,可以理解为将 (H,W)的featuremap 进行reshape为(H*W,)。
- BN:对N个数据在C维度上对进行数据的归一化,使用的均值方差 μ \mu μ、 σ \sigma σ 的shape为(1,1,1,C)。这样归一化时,batch内每个数据会互相影响,并在训练的过程中需要记录使用的 μ \mu μ 和 σ \sigma σ。
- LN:对N个数据,分别对每个数据的独立的进行归一化,使用的均值方差为batch内每个数据全部数值的均值方差。LN解耦了数据归一化时 batch间的影响,让每个数据的归一化独立起来,这样训练时无需统计均值方差,预测时单个数据独立归一化。公式为 μ n ( x ) = 1 C H W ∑ c = 1 C ∑ h = 1 H ∑ w = 1 W x n , h , w , c σ 2 ( x ) = 1 C H W ∑ c = 1 C ∑ h = 1 H ∑ w = 1 W ( x n , h , w , c − μ n ( x ) ) 2 \mu_n(x)=\frac{1}{CHW}\sum^{C}_{c=1}\sum^{H}_{h=1}\sum^{W}_{w=1}x_{n,h,w,c} \\ \sigma^2(x)=\frac{1}{CHW}\sum^{C}_{c=1}\sum^{H}_{h=1}\sum^{W}_{w=1}(x_{n,h,w,c}-\mu_n(x))^2 μn(x)=CHW1c=1∑Ch=1∑Hw=1∑Wxn,h,w,cσ2(x)=CHW1c=1∑Ch=1∑Hw=1∑W(xn,h,w,c−μn(x))2
在论文Group Normalization中提供了图片示意如下
在文本中,当文本的长短不一时,如何使用LN呢?
如下图,文本的长短不一,使得其不能在channel上做归一化,只能batch内对一个完整的句子独立的进行归一化,具体的为:一个句子中每个词在输入时特征向量长度为C,下图红颜色箭头为归一化的方向。
再次说明:LN使得各条数据间在进行标准化的时候相互独立。不需要保留训练过程中均值方差,推理时对单个句子进行归一化即可。
五、transformer的结构
5.1 ENCODER
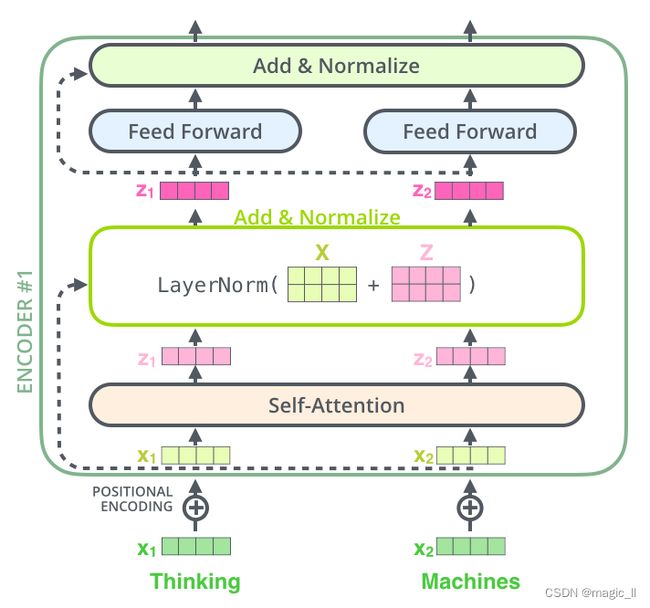
输入时token与positional encoding相加,送入到编码器结构中,会经过【self-attention】 --> 【残差】 -->【normalization】 --> 【feed forward】 --> 【normalization】。
将上面的结构进一步可视化:
这样的模块也是用与解码器。
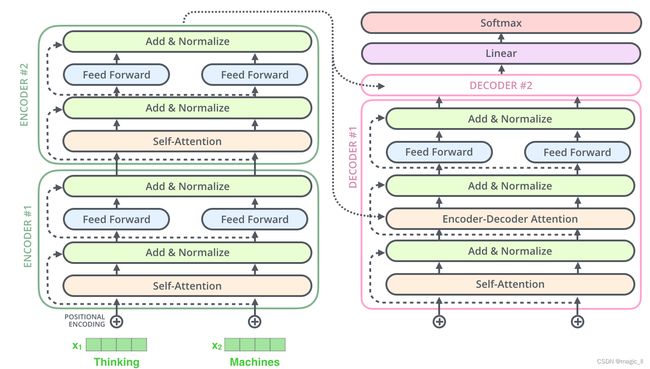
如果是由2个堆叠编码器和解码器组成的transformer,它的结构为:
5.2 DECODER
结构详细介绍:
- 【encoder】
【关键结构】self-attention。
【输入】 input_embedding+positional_encoding \text{input\_embedding+positional\_encoding} input_embedding+positional_encoding。
【输出】一组 KV。
【其他】在一个句子预测中,encoder仅执行一次即可。且与CNN不同的是,这里encoder的输出不是decoder模块的输入,而是作为decoder结构中的一个元素- 【decoder】
【self-attention】 --> 【残差】 -->【normalization】 --> 【cross-attention】 --> 【normalization】–>【feed forward】 --> 【normalization】。
【关键结构】self-attention、cross-attetion。
self-attention 的QKV与encoder中的一致,由上一层的输出计算而来。
cross-attention 中的Q来源于上一层,但KV来源于encoder模块的输出。具体的k/v是在 顶部编码器的输出转换为一组注意力向量K和V与一个可学习的矩阵相乘,而q是上一层的输出与可学习矩阵相乘。
【输入输出】预测第n个词时,输入为 (1,…n-1)个词的预测结果的 embedding+positional_encoding \text{embedding+positional\_encoding} embedding+positional_encoding作为decoder的输入。特别的,在预测第1个词时,将encoder中的输出为decoder的输入来源(因为此时没有实际的词输入,但该模块需要输入开启预测)。
【其他】decoder需要执行多次,本次之前的几次输出作为本次的输入。
具体的运行机制:
- 先将输入与position encoding 相加,然后送入encoder,得到一组KV 用于decoder中cross-attention模块中的KV的计算。
由于预测第一个词时,使用encoder的输出作为输入,送入decoder、linear+softmax,得到第一个词的outputs。
- 预测第二个词:将第一个预测结果的转化(embedding+position embedding)作为decoder的输入,预测第二个词。
- 预测第三个词:将第一二个预测结果的转化作为decoder的输入,预测第三个词。
- …
5.3 输出端的linear和softmax
这两层的作用,与CNN中的使用是一致的。
transformer在任务端侧,将单词的预测处理成了分类任务。假设模型知道10000个独立的英语单词(模型的"输出词汇表"),linear(全连接层)的输出为10000个维的logits向量,为在每个单词上的得分;然后再经过softmax层,将得分转换为概率,将概率最高的单词作为此次的输出。
五、补充:ResNet
resnet该篇论文个人也没有专门写一篇博客整理,就顺带在这里简单记录下。
在transformer中,每个模块都会使用残差连接residual connection。残差连接最开始是在2015年的ResNet中提出,用于解决深层网络训练问题。一开始是在图像任务中使用,现已经成为一种通用性的深度学习方法。5. 1 深的网络的使用
深度学习使用中,网络层数的增加面临问题:
- 计算资源的消耗
可通过GPU集群解决- 梯度消失和爆炸
因为网络层数太深,梯度反向传播中梯度累乘影响,容易导致浅层网络的参数发生 微弱的变化 或 较大的震荡,网络模型不收敛。可以用:
【数据标准初始化】统一输入数据的分布
【激活函数的更换】sigmoid让输出容易落在0~1区间的两端,从而引发梯度消失和爆炸,替换为relu可缓解
【BN的使用】使得每个网络层的输出在每个batch训练时,具有相对稳定的分布
【loss正则项】L1、L2等正则项都可改善梯度消失或爆炸的问题
【梯度裁剪】、【这里的残差结构】。- 网络过拟合
模型A比模型B在训练数据集上,性能更优,但A在验证集上性能更差。这是训练过拟合,最直接的办法就是丰富数据集、减小网络层数、增加BN。- 网络退化
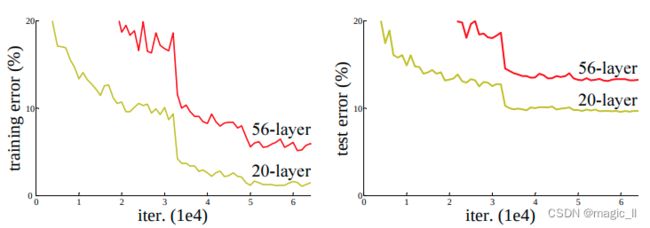
在模型能够收敛的情况下,网络越深,模型的准确率越低。这个情况我们称之为网络退化(Degradation)。如下图,网络结构56层的要比20层的在训练集和验证集上,都具有更高的错误率。
解决方法:ResNet能够有效的训练出更深的网络模型,同时深网络的表现不差于浅网络。
深度学习使用中,使用更深网络时的正确操作:
- 【使用深的网络的原因】模型越深,通常具有更强的表达能力。当模型训练时,数据集特征丰富,需和网络的表达能力相匹配。表达能力不够,会欠拟合;表达能力过强,同时数据特征相对简单,又容易过拟合,也会网络退化等问题。
- 【恒等映射的提出】我们想要增加网络的表达能力的同时,又要避免网络退化、网络过拟合。那么如何操作呢?
当我们实验了在CIFAR-10数据集上,56层网络比20层网络的表达能力更差时,只需要将56层中的多的36层网络置为恒等映射,这样就与20层网络具有相同的表现。
自适应层数数量的恒等映射,使得深的网络能够适应不同程度丰富度的数据集,从而得到相对应的表达能力。
5. 2 残差网络
残差结构
作者提出一个残差结构:一条支路用于恒等映射,一条支路用于正常的参数学习。 H(X)=F(x)+X \text{H(X)=F(x)+X} H(X)=F(x)+X。
- 当浅层网络时, F(X) \text{F(X)} F(X)只需学习输出与输入的偏移量的分布(偏移的数值一般小于输出的数据),这样可以得到一个更加精确的表达。
- 当深层网络时, F(X) \text{F(X)} F(X)会在优化目标的约束下,逼近于0(很难等于0),深层网络依然能学习到特征的同时,不会发生网络退化的问题。
残差网络
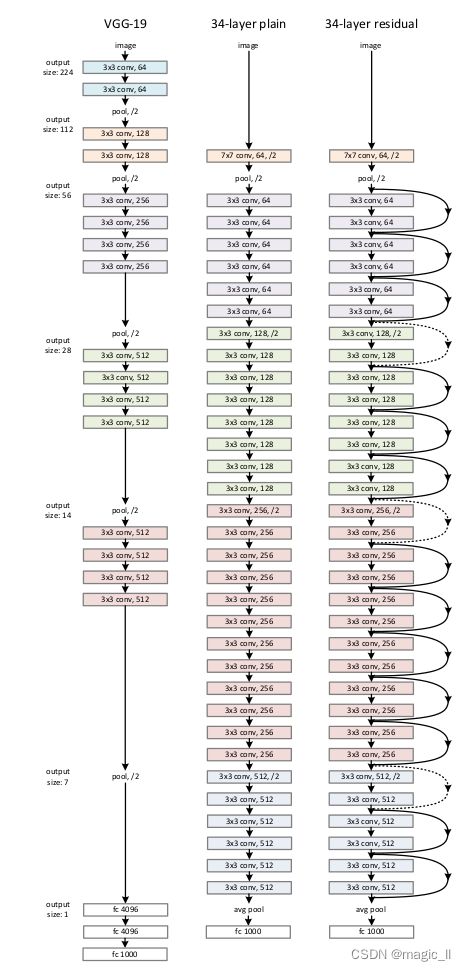
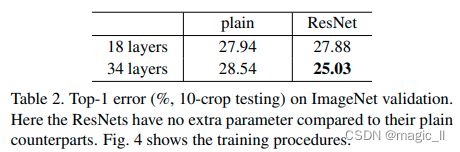
论文中做了较多的实验,其中34-layer plain和34-layer residule DNN。前者是一个标准的深层网络,后者是增加残差处理的深层网络。
实验结果如下图:
左图是18层和34层的plain DNN,右是18层和34层的residule DNN。粗线表示训练集上的错误率,细线表示验证集上的错误率。可以发现plain中,34层的错误率高于18层的,但在residule中,34层的错误率低于18层。说明残差结构起到了较好的效果。
链接记录:
https://jalammar.github.io/illustrated-transformer/
https://zhuanlan.zhihu.com/p/454482273
Batch Normalization原理与实战
深度学习基础 之 ---- BN、LN、IN、GN、SN