冒泡排序，选择排序，插入排序，快速排序的核心思想和代码实现

目录

1. 冒泡排序

1.1 冒泡排序的核心思想

1.2 冒泡排序代码展示

2. 选择排序

2.1 选择排序的核心思想

2.2 选择排序代码展示

3. 插入排序

3.1 插入排序的核心思想

3.2 插入排序代码展示

4. 快速排序

4.1 快速排序的核心思想

4.2 快速排序代码展示

---

1. 冒泡排序

1.1 冒泡排序的核心思想

如下图所示，是一个乱序的数组，冒泡排序的解题思路就是，让两个相邻数据作比较，把大的数据放在后边，小的数据放在前面，经过循环之后，最大的一个数据就已经在数组的最后了

过程如下：

（1）3和5作比较，后面的5大，不需要做交换；

（2）5和2作比较，前面的5大，5和2交换位置；

（3）5和1作比较，前面的5大，5和1交换位置；

 （4）5和4作比较，前面的5大，5和4交换位置； 

经过4次循环之后，最大的数据5已经确定并放在了数组的最后，我们也可以发现，5个数据，需要比较四次，那么类比推理，数组中如果有 n 个数据，则需要比较 n-1 次。

经过了第一次循环之后，最大的数据5此时在数组的最后，但是现在数组还不是完全有序的，我们只确定了最大的一个，其余的数据还需要继续使用冒泡排序，现在我们除去刚才的数据5，那么就剩下了4个数据需要进行排序，就需要进行 4 - 1 = 3 次，经过排序之后，我们又能确定数据4。

但是前面三个数据还是无序的，我们还要对前面三个数据再进行排序，进行3 - 1 = 2次排序，确定数据3；

确定了数据3的位置之后，还有两个数据需要排序，进行 2 - 1 = 1次排序，此时，整个数组才算是完全有序的；

1.2 冒泡排序代码展示

// 将冒泡排序定义为一个方法，方便调用，方法参数为待排序的乱序数组
    public static int[] bubbleSort(int[] arr) {
        // 定义一个第三方变量 temp 用于存储数组的值
        int temp;
        // 数组长度就是变量个数，一共要经历(数组长度 - 1)次循环
        // -1 另一方面是防止索引越界
        for (int i = 0; i < arr.length - 1; i++) {
            // 外层每循环一次，内层循环也可以少循环一次
            for (int j = 0; j < arr.length -1 - i; j++) {
                // 判断相邻两个数的大小
                if (arr[j] > arr[j+1]){
                    // 如果前面的数大于后面的书，交换两个数
                    temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
        // 经过两层循环之后，已经是有序数组，将数组进行返回
        return arr;
    }

2. 选择排序

2.1 选择排序的核心思想

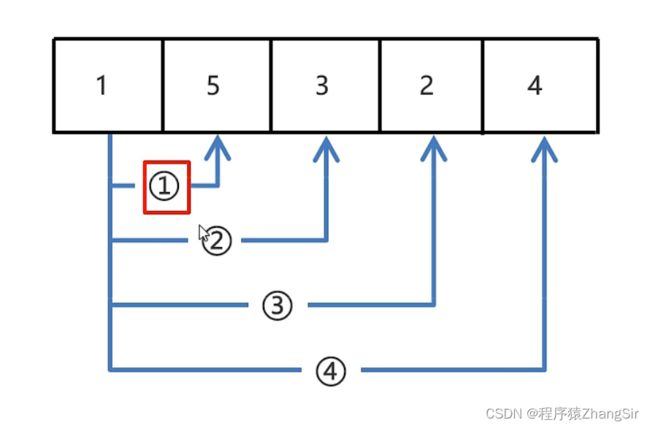
选择排序的思路也不难理解，例如下面的一个数组，选择排序是将0索引处的位置与后面的数据挨个进行比较，若小于后面的元素，则进行交换，经过一侧循环之后，数组中最小的元素就已经确定并且放在了数组的0索引处。

（1）第一次循环：0索引处的1分别于后面的4个数据进行比较，最后确定数字1最小，并放在0索引处；

（2）第二次循环：1索引处的5分别与后面的3个数据进行比较，最后确定2较小，并放在1索引处的位置；

（3）第三次循环：2索引处的数据3分别与后面的两个数据作比较，最后确定3最小并放在2索引处的位置；

（4）第四次循环：3索引处的数据5与后面的数据4作比较，确定4较小并放在3索引处的位置；

经过 n - 1次循环之后，整个无序的数组就变成了有序，达到了排序的目的。

2.2 选择排序代码展示

// 将选择排序定义为方法，方法参数为待排序数组，返回值为排好序的数组
    public static int[] selectSort(int[] arr) {
        // 定义一个第三方变量作为中转记录数组中的值
        int temp = 0;
        // 第一次循环，i = 0 取0索引处的值
        for (int i = 0; i < arr.length; i++) {
            // 内存循环第一次取1索引处的值与之作比较，比较后+1再取后面的值作比较
            // j = j + 1，说明外层循环每循环一次，内存循环就减少一次
            for (int j = i+1; j < arr.length; j++) {
                // 如果后面的值比前面的小，则进行交换
                if (arr[i] > arr[j]){
                    temp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = temp;
                }
            }
        }
        // 返回排好序的数组
        return arr;
    }

3. 插入排序

3.1 插入排序的核心思想

插入排序有点类似于我们平时打扑克整理牌，会把牌从小到大或者从大到小排列，会看起来更清爽更利于我们的出牌思路。

在插入排序中，我们可以把0索引的数或者0~N索引的数认为是有序的，把N+1到数组最后的数认定为无序的，然后依次遍历无序的数，把无序的每一个数插入到有序地数组中，当我们完整遍历一边数组之后，得到的数组就已经是有序数组了。

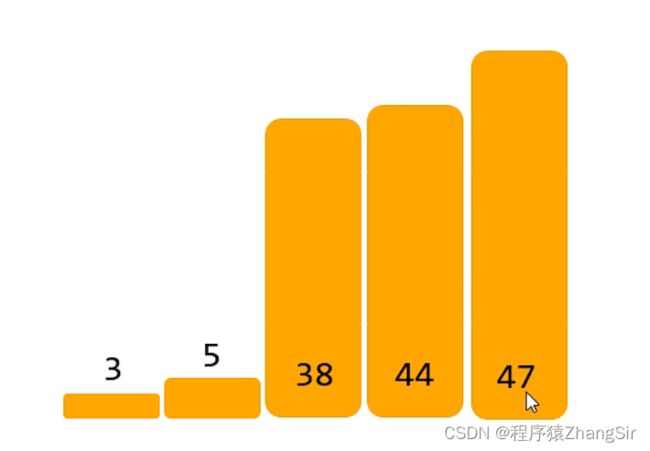
如下所示，有个五个随机数组，现在使用插入排序的思想对它们做排序。

（1）因为这里44本来就是有序的了，所以我就没有标记，44和3比较是第一步，这里我没有画；

（2）遍历得到38，拿38和 [3，44] 数组中的44作比较，比44小，再和3作比较，比3大，所以插入到3和44中间；

（3）遍历得到5，拿5和 [3，38，44] 数组后面的树比较，以此往前比，和上一步一样，直到确定5插入在3和38的中间，此时数组为 [3，5，38，44]；

（4）遍历的到47，拿47和 [3，5，38，44] 的44作比较，比44大，插入在最后，就可以得到一个有序数组了

3.2 插入排序代码展示

public static int[] selectSort(int[] arr){
        // 定义 i 为 1，直接从1索引处的值开始往后遍历
        for (int i = 1; i < arr.length; i++) {
            // 因为 i 一会还要用不能变，所以另外定义变量 j 记录 i 的值
            int j = i;
            // 定义一个临时变量 temp
            int temp;
            // 进入while循环，只要j不小于0或者arr[j]的值不小于arr[j-1] 的值，就一直向前比较
            while (j > 0 && arr[j] < arr[j-1]){
                temp = arr[j];
                arr[j] = arr[j-1];
                arr[j-1] = temp;
                j--;
            }
        }
        return arr;
    }

4. 快速排序

4.1 快速排序的核心思想

快速排序每次都可以确定一个数组中一个数的确定位置，我们首先遍历数组的0索引处的数，将它作为基准数，然后从数组两端开始遍历数组，比基准数小的全部放到左边，比基准数大的全部放到右边。

我来用一幅图展示这个过程，如下，是一个乱序的数组

 第一步：取出0索引的数字6，作为基准数

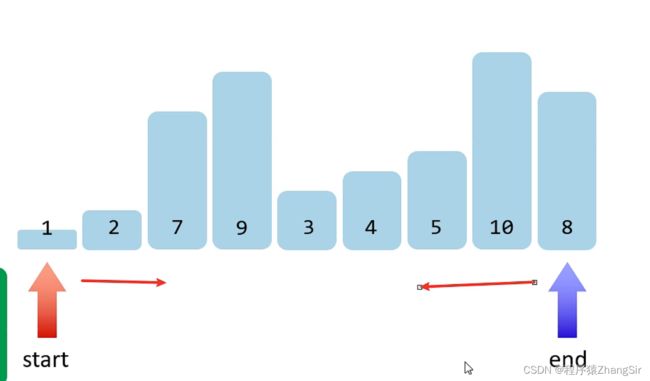
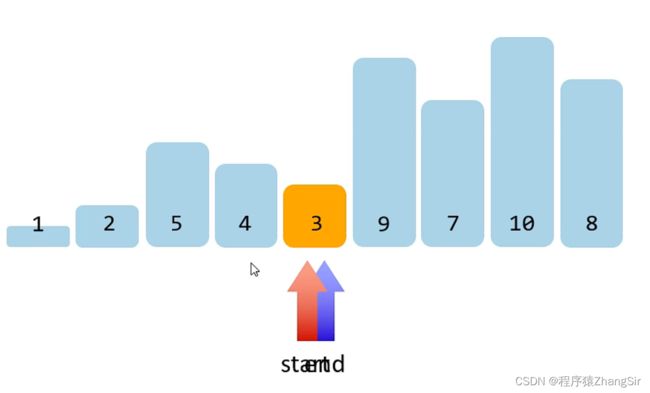
第二步：定义两个变量start和end，(也可以类比理解为指针)，start 从前往后遍历，end 从后往前便利；

第三步：start 负责找比基准数大的数，end 负责找比基准数小的数，如果不满足，就将指针向后移动一位，直到start与end相等；

 

第四步： start 经过三次循环，来到7，比6大，end 来到5，比6小；

 第五步：交换 start 和 end 处的值，如下；

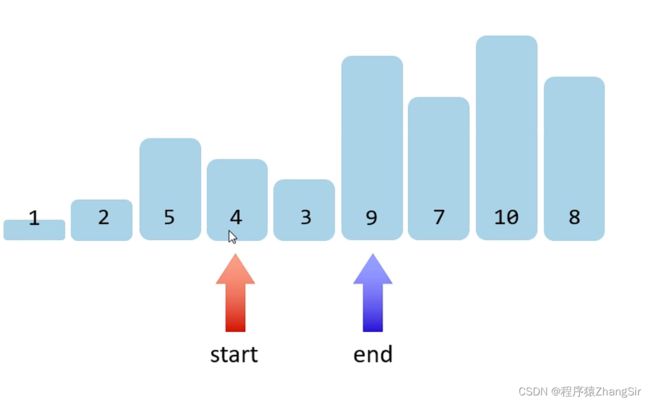
第六步：交换完毕5和7之后，因为 start 和 end 还没有碰面，继续找，再一次循环，start来到9，end 来到4，

 

第七步：将9和4做交换

 

 第八步：end 和 start 继续移动，在3的位置相遇，判断3 比6小；

第九步：交换我基准数6和3的位置；

第十步：此时我们再来观察，会发现基准数6前面的数都比6小，基准数6后面的数都比6大，所以此时6所处的位置就是有序数组中它应该待的位置；

然后我们以此类推，使用递归，就可以得到到最终的有序数组了；

4.2 快速排序代码展示

public static void main(String[] args) {
        // 定义一个数组
        int[] arr = {3,44,38,5,47};
        // 调用快速排序方法 
        quickSort(arr,0,arr.length-1);
        // for 循环输出排好序的数组结果
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+ ",");
        }
    }

    public static void quickSort(int[] arr,int i,int j){
        // 定义两个指针 start 和 end
        int start = i;
        int end = j;
        // 确定递归出口，不能无限递归，当 start 指针大于end 时，就要可以退出递归了
        if (start > end){
            return;
        }
        // 定义一个变量接收基准数
        int baseNumber = arr[i];
        // 定义一个变量作为中转变量
        int temp;
        // 开始循环，只要两个指针没有碰面，就一直循环
        while (start != end){
//  这里有一个点需要重点说明，必须让end指针先移动，start指针后移动，
// 否则会出现大于基准数的数据仍然在左边

            // end 指针开始从后往前遍历，进入while循环，
            while (true){
                // 每当有一个数小于基准数，就退出循环
                if (end <= start || arr[end] < baseNumber){
                    break;
                }
                // 如果不满足 if，end 指针向前移动一位
                end--;
            }
            // start 指针开始从前往后遍历，进入while循环，
            while (true){
                if (end <= start || arr[start] > baseNumber){
                    // 每当有一个数大于基准数，就退出循环
                    break;
                }
                // 如果不满足 if 条件，start 指针向后的移动一位
                start++;
            }
            // 两层while循环结束后，就会各自的到一个比基准数大的数和一个比基准数小的数，
            // 然后到 把 end 和 start 位置的数进行交换
            temp = arr[start];
            arr[start] = arr[end];
            arr[end] = temp;
        }
        // 大的while循环结束后，start和end相遇，
        temp = arr[i];
        arr[i] = arr[start];
        arr[start] = temp;
        // 递归调用自己，以确定位置的基准数分割点，将数组分为两半,
        // 此时start 代表基准数，所以stat-1就是数组左半边的最大值
        quickSort(arr,i,start - 1);
        // start + 1 就是数组右半边最小值
        quickSort(arr,start + 1,j);
    }

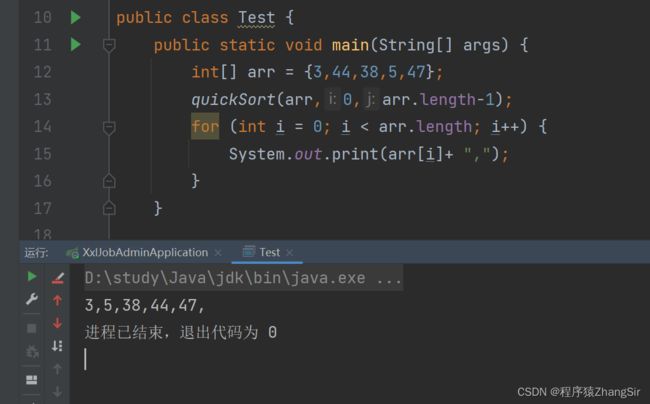
运行代码，就可以得到如下结果了，此时数组已经是有序的了。