leetcode:257. 二叉树的所有路径、104. 二叉树的最大深度、111. 二叉树的最小深度（JavaScript）

257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

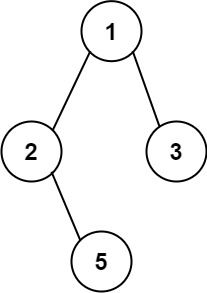
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

• 树中节点的数目在范围 [1, 100] 内
• -100 <= Node.val <= 100

思路：

递归遍历还用到了回溯的思想，每遍历到一个叶子节点就是一条路径，所以我们需要一个数组path来记录遍历的每个节点，当遇到叶子节点时，path中记录的就是到当前叶子结点的路径。当前路径遍历完，递归回溯的时候需要将path中最后一个元素弹出更新路径即可。

要点：

什么时候找到叶子结点？

当节点的左孩子和右孩子都为空时，当前节点为叶子结点，同时他也是递归终止条件。

if (!root.left && !root.right) {
        
        return;
}

为什么不判断当前节点是否为空？

因为在控制进入递归循环的时候会判断，所以能进入下一层递归的结点一定不为空。

// 若左子树不为空则进入递归
if (root.left) {
     path.push(root.val);
     dfs(root.left, res, path);
     path.pop();
}
// 若右子树不为空则进入递归
if (root.right) {
	path.push(root.val);
	dfs(root.right, res, path);
	path.pop();
}

完整代码

var binaryTreePaths = function(root) {
    const res = [], path = [];
    dfs(root, res, path);
    return res;
};
var dfs = function(root, res, path) {
     // 如果是叶子结点就记录路径
    if (!root.left && !root.right) {
        let s = '';
        for (const c of path) {
            s += c + '->';
        }
        // 因为叶子结点并没有进入path，所以要将叶子节点添加到路径上
        s += root.val;
        // 记录路径
        res.push(s);
        return;
    }
    // 处理左子树
    if (root.left) {
        path.push(root.val);
        dfs(root.left, res, path);
        path.pop();
    }
    // 处理右子树
    if (root.right) {
        path.push(root.val);
        dfs(root.right, res, path);
        path.pop();
    }
}

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

迭代

思路：采用层序遍历，每遍历一层深度就加一，这样一定回取到最大深度。

var maxDepth = function(root) {
    let deep = 0;
    if (!root) return 0;
    const que = [root];
    // 遍历每层元素
    while (que.length) {
        let len = que.length;
        // 记录每层元素的子元素
        while (len) {
            const tem = que.shift();
            tem.left && que.push(tem.left);
            tem.right && que.push(tem.right);
            len--;
        }
        // 遍历一层深度加一
        deep++;
    }
    return deep;
};

递归

思路：

在考虑使用哪一种递归顺序的时候，我发现前序和中序并不好统计深度，而后序遍历非常适合做本题。若当前节点为空，说明当前这一枝走到了最下面一层，则返回个父节点深度0，此时父节点取左右子树深度大的加一返回给自己的父节点，最后根节点就会收到其左右子树的深度，取更大的返回就能得到正确结果了。

var maxDepth = function(root) {
    if (!root) return 0;
    // 统计左子树深度
    const leftDeep = maxDepth(root.left);
    // 统计右子树深度
    const rightDeep = maxDepth(root.right);
    // 取深度更深的
    const deep = Math.max(leftDeep, rightDeep);
    // 将深度返回个当前元素的父元素
    return deep + 1;
};

如果不懂可以好好想一下。

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明： 叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

首先要明白什么是最小深度？最小深度是从根节点到最近叶子节点的最短路径上的节点数量。，注意是叶子节点。

迭代

思路：

采用层序遍历，在遍历每一层节点的时候判断它是否为叶子结点，如果是叶子结点就返回深度加一，为什么要加一呢？因为如下代码，深度加一是在遍历完当前一层节点后再进行的操作，所以在返回深度时需要在原来的基础上加上当前这一层。

var minDepth = function(root) {
    let deep = 0;
    if (!root) return 0;
    const que = [root];
    // 遍历每层元素
    while (que.length) {
        let len = que.length;
        // 记录每层元素的子元素
        while (len) {
            const tem = que.shift();
            tem.left && que.push(tem.left);
            tem.right && que.push(tem.right);
            // 若左右子节点都为空说明本节点是叶子结点
            if (!tem.left && !tem.right) return deep + 1;
            len--;
        }
        // 遍历一层深度加一
        deep++;
    }
    return deep;
};

递归

思路：

递归的思路与二叉树最大深度基本一致，只是将每次取更大深度变成了取更小的深度，还有当左子树为空时要返回右子树深度，右子树为空时要返回左子树深度，否则当根节点左子树为空右子树不为空时，就会返回1，也就是把根节点当成了叶子节点。

var minDepth = function(root) {
    if (!root) return 0;
    // 统计左子树深度
    const leftDeep = minDepth(root.left);
    // 统计右子树深度
    const rightDeep = minDepth(root.right);
    // 若根节点左子树为空，则返回右子树深度
    if (leftDeep === 0) return rightDeep + 1;
    // 若根节点左子树为空，则返回右子树深度
    if (rightDeep === 0) return leftDeep + 1;
    // 取深度更深的
    const deep = Math.min(leftDeep, rightDeep);
    // 将深度返回个当前元素的父元素
    return deep + 1;
};