hdu 1541 Stars poj 1195 Mobile phones(二维) poj 2155 Matrix(二维) hdu 3584 Cube(三维) 树状数组

 

/*
 * hdu1541.c
 *
 *  Created on: 2011-9-7
 *      Author: bjfuwangzhu
 */

#include<stdio.h>
#include<string.h>
#define nmax 32002
#define nnum 15002
int flag[nmax], count[nmax];
typedef struct point {
    int x, y;
} point;
point Point[nnum];
int lowbit(int x) {
    return x & (-x);
}
void modify(int pos) {
    while (pos < nmax) {
        flag[pos]++;
        pos += lowbit(pos);
    }
}
int query(int pos) {
    int sum;
    sum = 0;
    while (pos > 0) {
        sum += flag[pos];
        pos -= lowbit(pos);
    }
    return sum;
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("data.in", "r", stdin);
#endif
    int N, i;
    while (scanf("%d", &N) != EOF) {
        for (i = 0; i < N; i++) {
            scanf("%d %d", &Point[i].x, &Point[i].y);
        }
        memset(count, 0, sizeof(count));
        memset(flag, 0, sizeof(flag));
        for (i = 0; i < N; i++) {
            count[query(Point[i].x + 1)]++;
            modify(Point[i].x + 1);
        }
        for (i = 0; i < N; i++) {
            printf("%d\n", count[i]);
        }
    }
    return 0;
}

 

 

/*
 * poj1195.c
 *
 *  Created on: 2011-9-7
 *      Author: bjfuwangzhu
 */

#include<stdio.h>
#define nmax 1030
int num[nmax][nmax];
int lowbit(int x){
    return (x&(-x));
}
void  modefy(int x,int y,int value){
    int i,j;
    for(i=x;i<nmax;i+=lowbit(i)){
        for(j=y;j<nmax;j+=lowbit(j)){
            num[i][j]+=value;
        }
    }
}
int query(int x,int y){
    int i,j,res;
    for(i=x,res=0;i>0;i-=lowbit(i)){
        for(j=y;j>0;j-=lowbit(j)){
            res+=num[i][j];
        }
    }
    return res;
}
int main(){
#ifndef ONLINE_JUDGE
    freopen("data.in","r",stdin);
#endif
    int cas,N,value,i,j,x1,y1,x2,y2;
    while(scanf("%d",&cas)!=EOF&&(cas!=3)){
        switch(cas){
        case 0:
            scanf("%d",&N);
            for(i=0;i<nmax;i++){
                for(j=0;j<nmax;j++){
                    num[i][j]=0;
                }
            }
            break;
        case 1:
            scanf("%d %d %d",&x1,&y1,&value);
            x1++,y1++;
            modefy(x1,y1,value);
            break;
        case 2:
            scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
            x1++,y1++,x2++,y2++;
            printf("%d\n",query(x2,y2)-query(x1-1,y2)-query(x2,y1-1)+query(x1-1,y1-1));
            break;
        }
    }
    return 0;
}

引用于：http://hi.baidu.com/%BA%A3%CF%E0%C1%AC/blog/item/662a1ad19ef5c098a1ec9c78.html

原理很简单，就是三维树状数组模型。理解了三维树状数组，就可以直接秒杀。但是，三维的不好理解。只能由二维的去推广咯。

二维的如下（采自某大牛，感谢，膜拜v）：

模式二：随时修改数组 a[] 中某个区间的值(O(1))，查询某个元素的值(O(logn))

在这种模式下，a[i] 已经不再表示真实的值了，只不过是一个没有意义的、用来辅助的数组。这时我们真正需要的是另一个假想的数组 b[]，b[i] 才表示真实的元素值。但 c[] 数组却始终是为 a[] 数组服务的，这一点大家要明确。此时 Getsum(i) 虽然也是求 a[i] 之前的元素和，但它现在表示的是实际我要的值，也就是 b[i]。
比如现在我要对图1 中 a[] 数组中红色区域的值全部加1。当然你可以用模式一的 Modify(i) 对该区间内的每一个元素都修改一次，但如果这个区间很大，那么每次修改的复杂度就都是 O(nlogn)，m 次修改就是 O(mnlogn)，这在 m 和 n 很大的时候仍是不满足要求的。这时模式二便派上了用场。我只要将该区域的第一个元素 +1，最后一个元素的下一位置 -1，对每个位置 Getsum(i) 以后的值见图2：

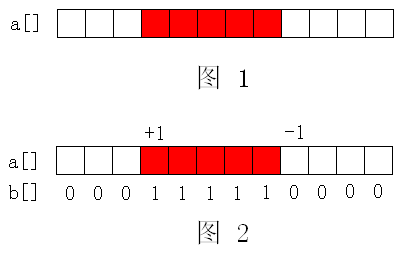
相信大家已经看得很清楚了，数组 b[] 正是我们想要的结果。模式二难理解主要在于 a[] 数组的意义。这时请不要再管 a[i] 表示什么，a[i] 已经没有意义了，我们需要的是 b[i]！但模式二同样存在一个缺陷，如果要对某个区间内的元素求和，就必须对该区间内的每个位置都作一次 Getsum(i)，求出所有位置的真实元素值然后累加，这样复杂度又变成 O(nlogn) 了。所以要分清两种模式的优缺点，根据题目的条件选择合适的模式，灵活应变！

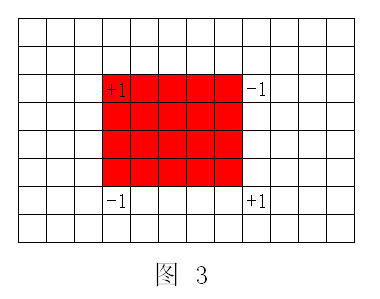
顺便给出二维树状数组模式二的修改方法：

 

/*
 * hdu3584.c
 *
 *  Created on: 2011-9-7
 *      Author: bjfuwangzhu
 */

#include<stdio.h>
#include<string.h>
#define nmax 110
int num[nmax][nmax][nmax];
int lowbit(int x) {
    return (x & (-x));
}
void update(int x,int y,int z,int value){
    int i,j,k;
    for(i=x;i<nmax;i+=lowbit(i)){
        for(j=y;j<nmax;j+=lowbit(j)){
            for(k=z;k<nmax;k+=lowbit(k)){
                num[i][j][k]+=value;
                }
            }
    }
}
int query(int x,int y,int z){
    int i,j,k,res;
    for(i=x,res=0;i>0;i-=lowbit(i)){
        for(j=y;j>0;j-=lowbit(j)){
            for(k=z;k>0;k-=lowbit(k)){
                res+=num[i][j][k];
            }
        }
    }
    return res;
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("data.in", "r", stdin);
#endif
    int N,M, i, j,k,x1,y1,z1,x2,y2,z2;
    while (scanf("%d %d", &N, &M) != EOF) {
        for(i=0;i<nmax;i++){
            for(j=0;j<nmax;j++){
                for(k=0;k<nmax;k++){
                    num[i][j][k]=0;
                }
            }
        }
        for (i = 0; i < M; i++) {
            scanf("%d", &j);
            if (j == 1) {
                scanf("%d %d %d %d %d %d",&x1,&y1,&z1,&x2,&y2,&z2);
                update(x1,y1,z1,1);
                update(x2+1,y1,z1,-1);
                update(x1,y2+1,z1,-1);
                update(x1,y1,z2+1,-1);
                update(x2+1,y2+1,z1,1);
                update(x1,y2+1,z2+1,1);
                update(x2+1,y1,z2+1,1);
                update(x2+1,y2+1,z2+1,-1);
            } else {
                scanf("%d %d %d",&x1,&y1,&z1);
                printf("%d\n",query(x1,y1,z1)&1);
            }
        }
    }
    return 0;
}

 

/*
 * poj2155.c
 *
 *  Created on: 2011-9-7
 *      Author: bjfuwangzhu
 */

#include<stdio.h>
#include<string.h>
#define nmax 1001
int num[nmax][nmax];
int lowbit(int x) {
    return (x & (-x));
}
void modefy(int x, int y, int value) {
    int i, j;
    for (i = x; i < nmax; i += lowbit(i)) {
        for (j = y; j < nmax; j += lowbit(j)) {
            num[i][j] += value;
        }
    }
}
int query(int x, int y) {
    int i, j, res;
    for (i = x, res = 0; i > 0; i -= lowbit(i)) {
        for (j = y; j > 0; j -= lowbit(j)) {
            res += num[i][j];
        }
    }
    return res;
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("data.in", "r", stdin);
#endif
    int T, N, M, i, j, x1, y1, x2, y2;
    char c;
    while (scanf("%d", &T) != EOF) {
        while (T--) {
            scanf("%d %d", &N, &M);
            for (i = 0; i < nmax; i++) {
                for (j = 0; j < nmax; j++) {
                    num[i][j] = 0;
                }
            }
            for (i = 0; i < M; i++) {
                scanf(" %c", &c);
                if (c == 'Q') {
                    scanf("%d %d", &x1, &y1);
                    printf("%d\n", query(x1, y1) & 1);
                } else {
                    scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
                    modefy(x1, y1, 1);
                    modefy(x2 + 1, y1, -1);
                    modefy(x1, y2 + 1, -1);
                    modefy(x2 + 1, y2 + 1, -1);
                }
            }
            if(T>0){
                printf("\n");
            }
        }
    }
    return 0;
}