图与遍历算法（1）——无向图

　　这是《计算机算法分析与设计》课件第二章“图与遍历算法”内容的总结。

　　一、关于无向图

　　1.无向图，简称图。图是一个三元组 G=( V, E, I ), 其中，V是顶点的集合，E是边的集合，而I是关联关系，它指明了 E 中的每条边与 V 中的每个顶点之间的关联关 系：每条边必定连接两个而且只有两个顶点，它们称为该边的端点。有边相连的 两个顶点称为相邻的。连接顶点v的边的条数称为v的度，记做 d(v). 图 G=( V, E, I )中顶点的度与边数有如下的 Euler 公式：

　　所有顶点的度数=2*边数

　　2.简单图：没有重复边的图。n 阶完全图是指具有 n 个顶点而且每两个顶点 之间都有边连接的简单图。

　　另一类特殊的图是偶图（也叫二部图），它的顶点集分成两部分V1，V2，每部分中的顶点之间不相连（没有边连接）

　　　　　　

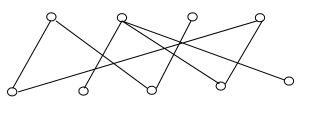
　　 k-部图，是指图的顶点集被分成 个部分，每部分中的顶点之间没有边相连。

　　3.邻接矩阵和关联矩阵。前者用来表示顶点与顶点之间的邻接关系，后者用来表示顶点与边之间的关联关系。

　　 4.图的另一个重要概念是路径，区分为途径、迹和路（重点掌握、区分） 

　　途径：顶点与边交叉出现的序列。迹是指边不重复的途径，而顶点不重复的途径称为路。 起点和终点重合的途径称为闭途径，起点和终点重合的迹称为闭迹，顶点不重复的闭迹称为圈。没有圈的图称为森林。

　　5. 如果 G 是具有 n 个顶点、m 条边的图，则下列结论成立：（注意前三和后二的等价关系）

　　① 若 G 是树， 则 m = n-1；

　　② 若 G 是连通图，而且满足 m = n-1，则 G 是树；

　　③ 若 G 不包含圈，而且满足 m = n-1，则 G 是树；

　　④若 G 是由 k 棵树构成的森林，则 m = n-k ；

　　⑤若G有k个连通分支，而且满足m = n-k，则G是森林。