### EM算法
EM算法学习。
#@author: gr
#@date: 2014-101-21
#@email: [email protected]一、 Jensen不等式
convex function:
外国的凸函数(convex)和同济大学的教程正好相反,$x^2$在国外是凸函数。
$$convex ~~ function => \left\{ \begin{array}{c} 若 ~f 是函数,则f''(x)\ge 0 \\ 若x是向量时,hessian矩阵H是半正定的 \end{array} \right.$$
Jesen不等式:
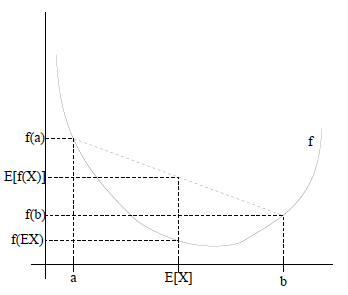
若 $f$ 是凸函数(convex function), $x$ 是随机变量,则有不等式 $E[f(x)] \ge f(E[x])$ 成立。
同理,若 $f$ 是凹函数, $x$ 是随机变量,则有不等式 $E[f(x)] \le f(E[x])$ 成立。
如下图所示, 凸函数满足 $E[f(x)] \ge f(E[x])$ :
二、 EM算法
引入:
最常见的例子就是男女生身高问题。假设男女生身高符合高斯分布,实际上单独测量男生或女生身高可以用高斯分布很好地得出结果。
但现在的问题时,给你一堆数据,你并不知道这个数据是男还是女的,所以你无法推断这个分布,因为男女生是符合两个不同的分布,这也就是混合高斯模型了。这里就需要引入是男是女这个隐藏变量,如果知道这个隐藏变量的值,那下面的求解过程就很简单了。
推导:
假设有样本集 ${x_1, x_2, \cdots , x_m }$共 $m$ 个样本,但每个样本对应的类别 $z_i$ 是未知的,也即隐变量。现在要求估计参数 $\theta$,如果没有隐变量 $z$,可以使用极大似然估计参数,如下:
$$ \arg \max_\theta \Pi_i p(x_i;\theta ) = \arg \max_\theta \sum_i \log p(x_i;\theta)$$
现在的问题是,包含一个隐变量 $z$,如下:
$$\sum_i \log p(x_i; \theta) = \sum_i \log \sum_{z_i} p(x_i, z_i ; \theta)$$
怎么做呢,直接对这个似然函数求导,因为含有隐变量,计算十分困难。这时,前人想出了用上面讲的Jensen不等式,分子分母同乘$Q(z_i)$,$Q(z_i)$是隐变量$z$满足的分布,凑出了Jensen不等式形式,如下:
$$\begin{align*} \sum_i \log \sum_{x_i} p(x_i, z_i; \theta) = & \sum_i \log \sum_{z_i} Q(z_i) \dfrac{p(x_i, z_i; \theta)}{Q(z_i)} ~~~~~~~~(1)\\ \ge & \sum_i \sum_{z_i} Q(z_i) \log \dfrac{p(x_i, z_i ; \theta)}{Q(z_i)} ~~~~~~~~(2)\end{align*}$$
这是面, 函数 $f$ 是一个$log$,它是一个凹函数,有 $f(E[x]) \ge E[f(x)]$。
优化问题:
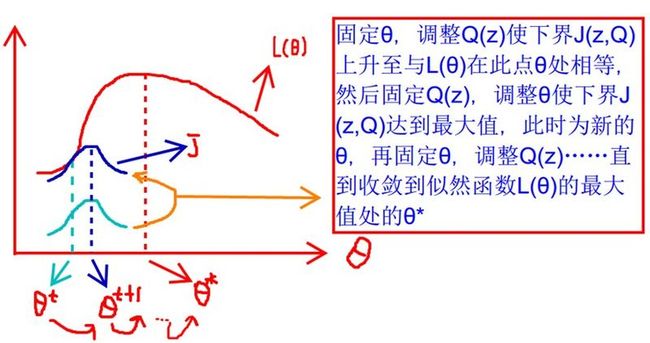
上式的关系可以写为 $L(\theta) \ge J(z, \theta)$ 。我们要求式(1)的最大值,但式(2)的最大值并不等于它的最大值。
那么如何求解呢,我们通过不断提升$J(z, \theta)$的上界来逼近$L(\theta)$。
下图来自博客 。首先,固定 $\theta$, 使 $J$ 提升到与 $L(\theta)$ 相同的高度。然后调整 $\theta$,最大化 $J$ 后,得到一个新的 $\theta$,再固定这个 $\theta$,提升 $J$,如此反复,最终就得到最优化解 $\theta^*$。
现在还有个问题是如何提升 $J(z, \theta)$ 与 $L(\theta)$ 相同的高度。我们考虑 Jensen不等式在固定点$\theta$取等号时,要让随机变量变成常数值,需要满足如下式子:
$$\dfrac{p(x_i, z_i ; \theta)}{Q_i(z_i)} = c$$
因为$\sum_z Q_i(z_i) = 1$,那么有 $\sum_z p(x_i, z_i; \theta) = c$,那么有下式:
$$\begin{align*} Q_i(z_i) = & \dfrac{p(x_i, z_i; \theta)}{c} \\ = & \dfrac{p(x_i, z_i; \theta)}{\sum_z p(x_i, z; \theta)} \\ = & \dfrac{p(x_i, z_i; \theta)}{p(x_i; \theta)} \\ = & p(z_i \mid x_i; \theta)\end{align*}$$
这样在固定 $\theta$ 后,我们知道使下界提升的 $Q(z)$ 的计算公式就是后验概率。这也就是E步求期望。
那么总结一下,EM算法的一般分两步:
E步:
根据初始参数或上一次迭代的参数计算出隐性变量的后验概率,也就是隐性变量的期望。作为隐藏变量的现估计值:
$$Q_i(z_i) := p(z_i \mid x_i; \theta)$$
M步:
将似然函数最大化以获得新的参数值:
$$\theta := \arg \max_\theta \sum_i \sum_{z_i} Q_i(z_i)\log\dfrac{p(x_i, z_i; \theta)}{Q_i(z_i)}$$
不断迭代上面两个步骤,就可以得到最大似然估计。那么,为什么能保证以上的两个步骤一定收敛呢?
因为估计是单调增加的,最终会收敛到最大似然估计的估计值。
$$\begin{align*} l(\theta^{t + 1}) \ge & \sum_i \sum_{z_i} Q_i^t(z_i) \log \dfrac{p(x_i, z_i; \theta^{t+1})}{Q_i^t(z_i)} \\ \ge & \sum_i \sum_{z_i}Q_i^t(z_i)\log \dfrac{p(x_i, z_i;\theta^t)}{Q_i^t(z_i)} \\ = & l(\theta^t)\end{align*}$$