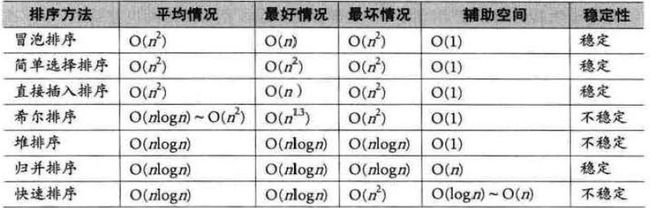
冒泡排序、简单选择排序、直接插入排序、希尔排序

 

冒泡排序（Bubble Sort）的基本思想：两两比较相邻记录的关键字，如果反序则交换，直到没有反序的记录为止。时间复杂度为O（n²）.

简单选择排序（Simple Selection Sort）的基本思想：通过n-i次关键字之间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i个记录交换。应该说，尽管与冒泡排序同为O(n²)， 但简单选择排序的性能上还是要略优于冒泡排序。

直接插入排序（Straight Insertion Sort）的基本思想：将一个记录插入到前面已经排序好的有序表中，从而得到一个新的、记录数不断加1的有序表。直接插入排序法的时间复杂度为O(n2) 。从这里也看出，同样的O(n²)时间复杂度，直接插入排序法比冒炮和简单选择排序的性能要好一些。

希尔排序（Shell Sort）的基本思想：将相隔某个增量的记录组成一个子序列，在这些子序列内分别进行直接插入排序，得到基本有序的序列，最后在将增量为1的记录（即整个序列）的进行一次直接插入排序。其实希尔排序就是直接插入排序的改进。大量的研究表明，当增量序列为dlta[k]=2^t-k+1-1 ( 0 <=k<=t <= [log₂ (n+l)])时，可以获得不错的效率， 其时间复杂度为O(n^3/2，要好于直接排序的o(n²)。需要注意的是， 增量序列的最后一个增量值必须等于1 才行。另外由于记录是跳跃式的移动，使得排序的效率提高，但也使得希尔排序并不是一种稳定的排序算法。

堆排序(Heap Sort) 的基本思想是：将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根结点。将官移走(其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值) .然后将剩余的n - 1 个序列重新构造成一个堆，这样就刽寻到n 个元素中的次小值。如此反复执行， 便能得到一个有序序列了。其实，堆排序就是对简单选择排序进行的一种改进，这种改进效果是非常明显的。堆排序的时间复杂度是O（nlogn）。由于堆排序对原始记录的排序状态并不敏感，因此它无论是最好、最坏和平均时间复杂度均为O(nlogn) 。这在性能上显然要远远好过于冒泡、简单选择、直接插入的O(n²)的时间复杂度了。

快速排序（Quick Sort）的基本思想是：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行同样的排序，依次递归达到整个序列有序的目的。对于枢轴pivot的选取可以采用三数取中（median of three）法，即取三个关键字先进行排序，将中间作为枢轴，一般是取左端、右端和中间三个数，也可以随机选取。对于待排序列较长的，可采用九数取中的方法。此外，还可以优化一些不必要的交换。优化小数组的排序，即当序列较长时采用快排，较短时采用直接插入排序，设置一个阈值就可以了。快速排序算法经过多次的优化之后，在整体性能上，依旧是排序算法的王者。

归并排序( Merging Sort) 的基本思想是：假设初始序列含有n 个记录， 则可以看成是n 个有序的子序列，每个子序列的长度为1 ，然后两两归并，得到[n/2] <[x]表示不小于x 的最小整数)个长度为2 或1 的有序子序列;再两两归并，……，如此重复， 直至得到一个长度为n 的有序序列为止，这种排序方法称为2 路归并排序.

 

 

  1 //冒泡排序、简单选择排序、直接插入排序
  2 #include "stdafx.h"
  3 
  4 #include "stdio.h" 
  5 #define TRUE 1 
  6 #define FALSE 0
  7 #define MAX_LENGTH_INSERT_SORT 5
  8 
  9 void bubblesort(int *list, int index);
 10 void selectsort(int *list, int index);
 11 void insertsort(int *list, int index);
 12 void shellsort(int *list, int index);
 13 void heapsort(int *list, int index);
 14 void heapadjust(int *list, int s, int m);
 15 void quicksort(int *list, int index);
 16 void Qsort(int *list, int low, int high);
 17 int partition(int *list, int low, int high);
 18 
 19 typedef int status;
 20 int list[20];    //默认最大长度为20
 21 int temp;
 22 int i, j;
 23 int node;
 24 status change = TRUE;
 25 
 26 void swap(int *list, int i, int j)//交换元素
 27 {
 28     temp = list[i];
 29     list[i] = list[j];
 30     list[j] = temp;
 31 }
 32 
 33 void main(void)
 34 {
 35     int index = 0;
 36     printf("Please input the value you want to sort(exit for 0):\n");
 37     scanf_s("%d", &node);
 38     while (node != 0)
 39     {
 40         list[index] = node;
 41         index += 1;
 42         scanf_s("%d", &node);
 43     }
 44     bubblesort(list, index);
 45     selectsort(list, index);
 46     insertsort(list, index);
 47     shellsort(list, index);
 48     heapsort(list, index);
 49     quicksort(list, index);
 50 }
 51 
 52 void bubblesort(int *list, int index) //冒泡排序 时间复杂度O（n2）
 53 {
 54     for (j = 0; j<index && change; j++)
 55     {
 56         change = FALSE;
 57         for (i = 1; i<index - j; i++)
 58         {
 59             if (list[i - 1]>list[i])
 60             {
 61                 swap(list, i - 1, i);
 62                 change = TRUE;
 63             }
 64         }
 65     }
 66     printf("\n冒泡排序后为：    ");
 67     for (i = 0; i < index; i++)
 68     {
 69         printf("%d ", list[i]);
 70     }
 71 
 72 }
 73 
 74 void selectsort(int *list, int index)//简单选择排序  时间复杂度O（n2）
 75 {
 76     int min;
 77     for (i = 0; i < index - 1; i++)
 78     {
 79         min = i;
 80         for (j = i + 1; j < index; j++)
 81         {
 82             if (list[i]>list[j])
 83             {
 84                 min = j;
 85             }
 86             if (min != i)
 87             {
 88                 swap(list, min, i);
 89             }
 90         }
 91     }
 92     printf("\n简单选择排序后为：");
 93     for (i = 0; i < index; i++)
 94     {
 95         printf("%d ", list[i]);
 96     }
 97 }
 98 
 99 void insertsort(int *list, int index)//直接插入排序  时间复杂度O（n2）
100 {
101     for (i = 1; i < index; i++)
102     {
103         if (list[i - 1]>list[i])
104         {
105             temp = list[i];
106             for (j = i; j >= 1 && list[j-1] > temp ;j--)
107             {
108                 list[j] = list[j - 1];
109             }
110             list[j] = temp;
111         }
112     }
113     printf("\n直接插入排序后为：");
114     for (i = 0; i < index; i++)
115     {
116         printf("%d ", list[i]);
117     }
118 }
119 void shellsort(int *list, int index)   //希尔排序  时间复杂度为O（nr），（1<r<2）
120 {
121     int length = index;
122     while (length>1)
123     {
124         length = length / 3 + 1;       //间隔长度
125         for (i = length; i < length; i++)
126         {
127             if (list[i] < list[i - length])
128             {
129                 temp = list[i];
130                 for (j = i - length; j >= 0 && list[j]>temp; j -= length)
131                 {
132                     list[j + length] = list[j];      //这一行的j比下一行的j大length
133                 }
134                 list[j + length] = temp;            //这一行的j比上一行的j小length
135             }
136         }
137     }
138     printf("\n希尔排序后为：    ");
139     for (i = 0; i < index; i++)
140     {
141         printf("%d ", list[i]);
142     }
143 }
144 
145 void heapsort(int *list, int index)//堆排序  时间复杂度为O（nlogn）  不稳定排序
146 {
147     for (i = index / 2; i>0; i--)
148     {
149         heapadjust(list, i , index);
150     }
151     for (i = index; i > 1; i--)
152     {
153         swap(list, 0, i-1);
154         heapadjust(list, 1, i - 1);
155     }
156     printf("\n堆排序后为：      ");
157     for (i = 0; i < index; i++)
158     {
159         printf("%d ", list[i]);
160     }
161 }
162 
163 void heapadjust(int *list, int s, int m)   //生成大顶堆
164 {
165     temp = list[s-1];                     //数组list是从0开始，而堆是从1开始，所以要减1；
166     for (j = 2 * s; j <= m; j *= 2)
167     {
168         if (j < m && list[j - 1] < list[j])  //比较结点左孩子和右孩子的大小
169             ++j;
170         if (temp >= list[j - 1])     //比较孩子中的较大者和结点的大小
171             break;
172         list[s - 1] = list[j - 1];    //交换
173         s = j;
174     }
175     list[s - 1] = temp;//插入；
176 }
177 
178 void quicksort(int *list, int index)//快速排序，冒泡排序的升级版 时间复杂度O(nlogn)
179 {
180     Qsort(list, 0, index - 1);
181     printf("\n快速排序后为：    ");
182     for (i = 0; i < index; i++)
183     {
184         printf("%d ", list[i]);
185     }
186 }
187 void Qsort(int *list, int low, int high)
188 {
189     int pivot;
190     if (low < high)//if((high-low)>MAX_LENGTH_INSERT_SORT),优化，当high-low大于某个常数时用快速排序
191     {
192         pivot = partition(list, low, high);
193 
194         Qsort(list, low, pivot - 1);
195         Qsort(list, pivot + 1, high);
196     }
197     //else
198         //insertsort(list, high-low);
199 }
200 int partition(int *list, int low, int high)
201 {
202     int pivotkey;
203 
204     int m = low + (high - low) / 2;//三数取中法  ，对于较大的待排序列可使用九数取中
205     if (list[low] > list[high])
206     {
207         swap(list, low, high);
208     }
209     if (list[m] > list[high])//交换中间和右端，保证中间较小
210     {
211         swap(list, m, high);
212     }
213     if (list[m] > list[low])//交换中间和左端，保证中间值放在low位置
214     {
215         swap(list, m, low);
216     }
217 
218     pivotkey = list[low];
219     //temp=pivotkey;
220     while (low < high)
221     {
222         while (low < high&&list[high] >= pivotkey)
223         {
224             high--;
225         }
226         swap(list, low, high);
227         //list[low]=list[high];   //采用替换而不交换，减少不必要的交换
228         while (low < high&&list[low] <= pivotkey)
229         {
230             low++;
231         }
232         swap(list, low, high);
233         //list[high]=list[low];  //采用替换而不交换，减少不必要的交换
234 
235     }
236     //list[low]=temp;
237     return low;
238 
239 }