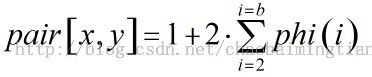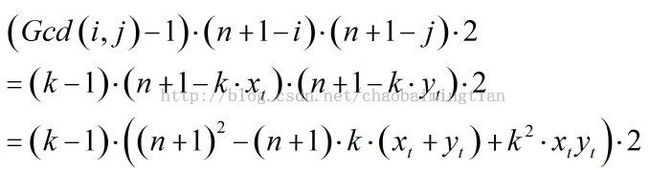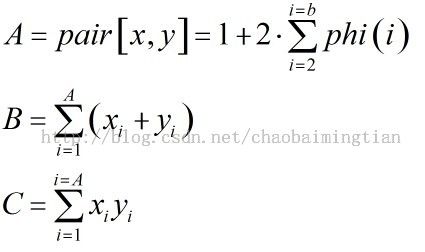HDU 4483 Lattice triangle(欧拉函数)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4483
题意:给出一个(n+1)*(n+1)的格子。在这个格子中存在多少个三角形?
思路:反着想,所有情况减去不是三角形的。下面计算不是三角形的。
(1)我们用C(n,m)表示组合数。考虑共线,一共有C((n+1)*(n+1),3)种情况。然后,要减去共线的情况。首先,三个点在同一行或者同一列,这种情况有2*(n+1)*C(n+1,3);最后就是斜着共线的情况;
(2)对于斜着共线的情况,我们可以枚举两个端点,然后看这两个端点之间有多少个点。我们发现,我们枚举两个端点时其实就是枚举一个小矩形的两个相对的顶点,我们知道,设矩形长宽为x,y,那么矩形对角线上有Gcd(x,y)+1个点,除去两个端点,中间有Gcd(x,y)-1个点。所以此次枚举需要减去的三角形个数为(Gcd(x,y)-1)*2。为啥乘以2呢?因为矩形的另外一个对角线也是相同的。接着,我们发现,这样的三角形一共有(n+1-x)*(n+1-y)个,所以枚举x、y时需要减去的总数为:(Gcd(x,y)-1)*(n+1-x)*(n+1-y)*2,因此,我们可以这样计算斜线共线的个数:
这个复杂度是O(n^2)的。下面我们优化这个计算过程。我们现在直接枚举i和j的Gcd值,设为k,即Gcd(i,j)=k,那么Gcd(i/k,j/k)=1,令a=i/k,b=j/k,那么对于当前的k我们首先看有多少组(x,y)满足Gcd(x,y)=k,也就是多少组 (x,y)满足gcd(x,y)=1,x<=a,y<=b,由于对称性,我们不妨设a<=b,那么此时(x,y)的对数就是:
其中,那个1表示(x,y)=(1,1),后面的phi表示欧拉函数,乘以2是因为x和y的对称性,我们此时是假设的a<=b,也即x<y(注意除了开始的(1,1)后面不会有x=y 的,因为Gcd(x,y)=1),x和y是可以交换位置的。这样对于某个k我们就求出了有多少对(x,y)满足Gcd(x,y)=k。接着,我们看上面那个式子:
因为满足Gcd(x,y)=k的(x,y)的对数已经计算出来。而上面的式子中是指对于其中的某一对(x,y)计算的,我们令式子中(n+1)^2、(n+1)*K、k^2的系数分别为A、B、C,那么有:
其中phi容易计算。那么B和C怎么计算呢?对于n,若Gcd(n,m)=1,那么Gcd(n,n-m)=1。也就是与n互质的数字是成对出现的,而且和为n。所以[1,n]中与n互质的数字之和为:phi[n]/2*n。这样,就能使用phi计算出B和C了。
i64 A[N],B[N],C[N],phi[N];
void init()
{
A[1]=C[1]=1; B[1]=2;
int i,j;
phi[1]=1;
for(i=2;i<N;i++) if(!phi[i])
{
for(j=i;j<N;j+=i)
{
if(!phi[j]) phi[j]=j;
phi[j]-=phi[j]/i;
}
}
for(i=2;i<N;i++)
{
A[i]=(A[i-1]+phi[i]*2)%mod;
B[i]=(B[i-1]+phi[i]*i*3)%mod;
C[i]=(C[i-1]+phi[i]*i%mod*i)%mod;
}
}
i64 n;
int C3(i64 x)
{
if(x<=2) return 0;
i64 a=(x-1)%mod,b=(x-2)%mod,c=166666668;
return x%mod*a%mod*b%mod*c%mod;
}
i64 M(i64 x,i64 y,i64 z)
{
return x*y%mod*z%mod;
}
int main()
{
init();
rush()
{
RD(n);
i64 ans=C3((n+1)*(n+1))-2*(n+1)*C3(n+1)%mod;
i64 temp=0;
i64 i,k;
for(i=2;i<=n;i++)
{
k=n/i;
temp+=(i-1)*(M(n+1,n+1,A[k])-M(n+1,i,B[k])+M(i,i,C[k]))%mod;
temp%=mod;
}
ans-=temp*2;
ans=(ans%mod+mod)%mod;
PR(ans);
}
return 0;
}