Why one-norm is an agreeable alternative for zero-norm?

 

【转载请注明出处】http://www.cnblogs.com/mashiqi

 

Today I try to give a brief inspection on why we always choose one-norm as the approximation of zero-norm, which is a sparsity indicator. This blog is not rigorous in theory, but I just want give a intuitive explanation. It may be extended to be more comprehensive in the future.

I begin to know something about zero-norm totally from the emergence of the so-called Compressive Sensing theory. While CS brings us a bunch of encouraging tools to handle some problems, such as image denoising, we also know that it is hard to operate directly on the zero-norm (in fact it is NP-hard). Therefore many scholars regard one-norm as an agreeable alternative for zero-norm! But why one-norm, why isn't two-norm or other?

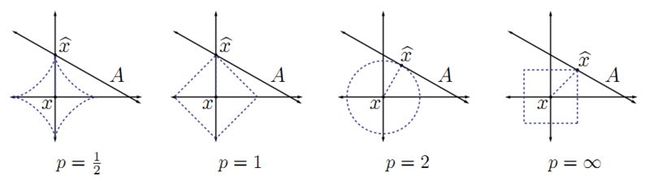
There is a picture (with some small modefication for my own usage) from [Davenport et al. 2011] that gives a illustrative explanation of what I want to express.

We see that the intersection $\hat{x}$ when $p=1/2$ is equivalent to $\hat{x}$ when $p=1$--both are the intersection of solid line and y-axis. But the corresponding intersection of $p=2$ and $p=\infty$ is not so--they are in somewhere out of any axis. Further, for the first two intersections each is only have one coordinate that is non-zero, and $0 \leq p \leq 1$. Then I give my intuitive explanation of the main question of this blog: the shape of the contour of some critical points, such as intersections of unit circle and axes, of the $l_p$ space attributes a lot to the sparsity of the solution of an algorithm performed in this $l_p$ space, and these intersections is like a sharp vertex when $0 \leq p \leq 1$, while they are dull when $p > 1$. I'll show this a simple mathematical example.

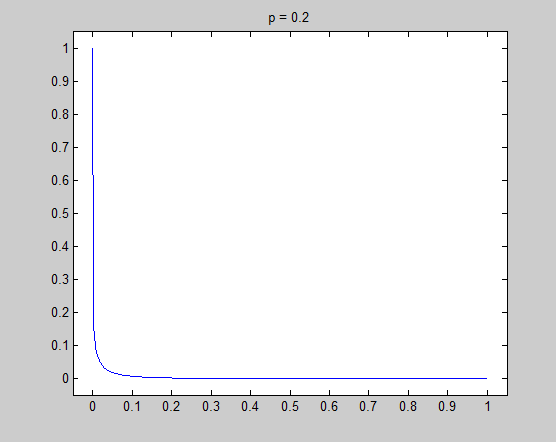
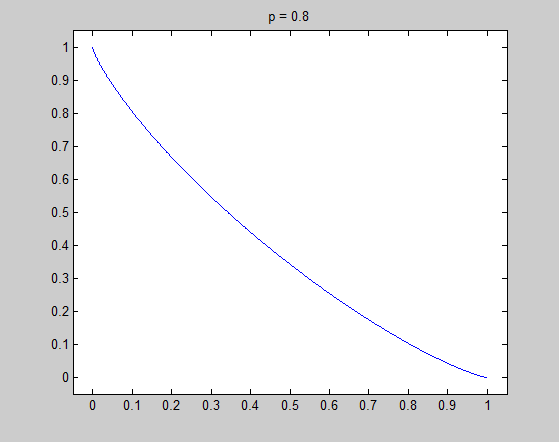
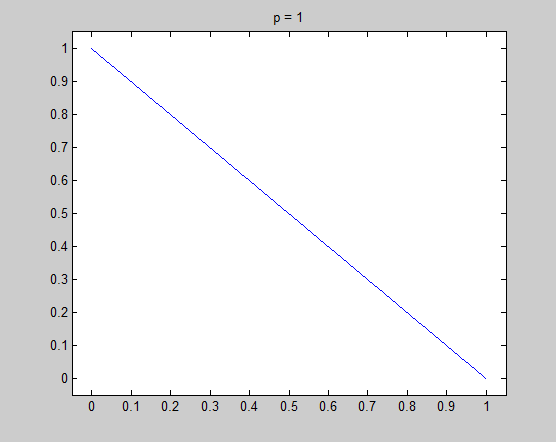
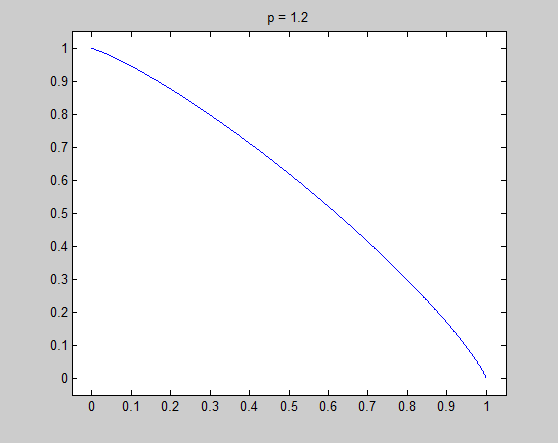
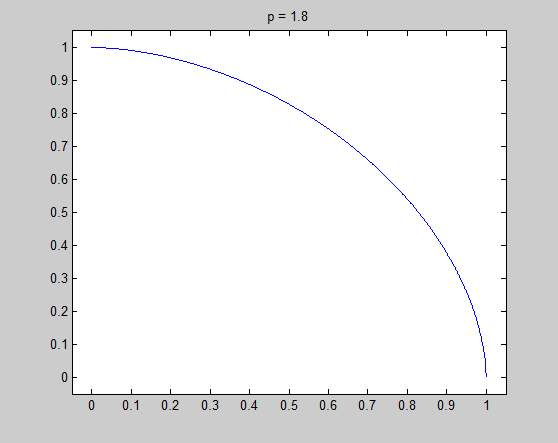
Let's consider the $l_p$ unit cirle in two-dimensional space: $$\|(x,y)\|_p = (x^p + y^p)^{1/p} = x^p + y^p = 1,~(p \geq 0)$$ For simplicity, I only plot the unit cirle in the first quadrant ($y = (1 - x^p)^{1/p},~(x \geq 0, y \geq 0)$):

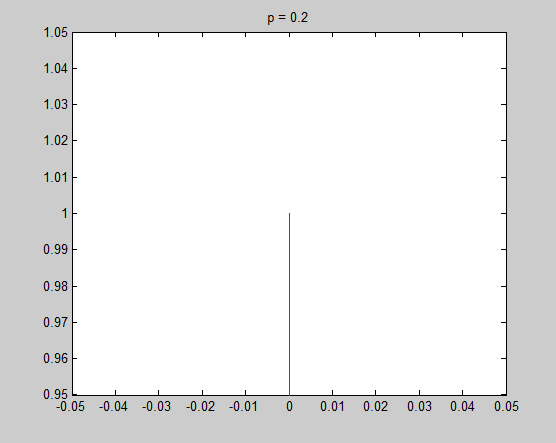
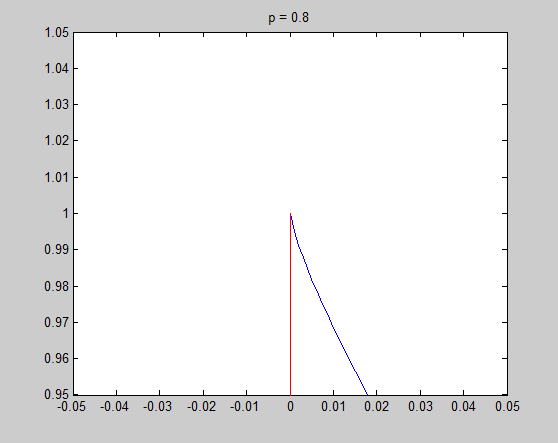
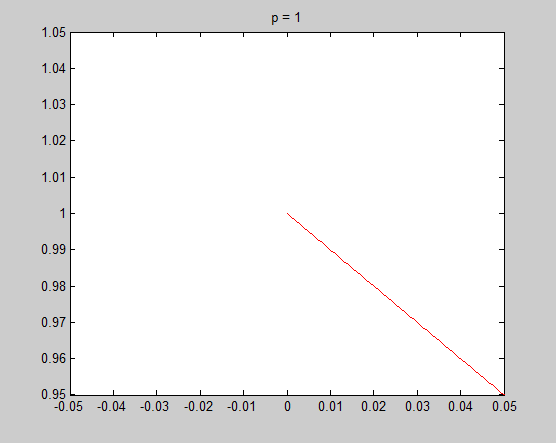
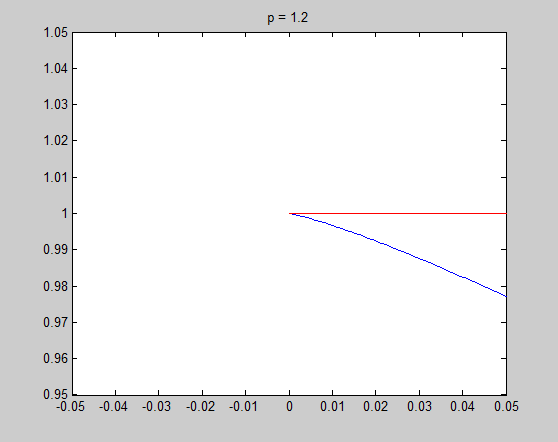
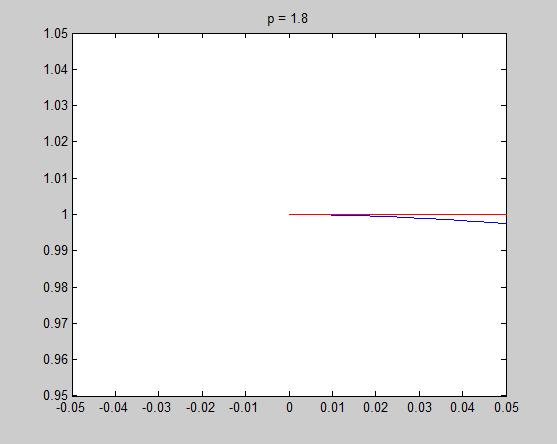
It is very necessary to investigate the detail around $x=0$, and the tangential of the unit circle in that point is the key point to understand my intuitive explanation. Now let's see the detail and the tangential in $x=0$ to see what happened there.

In these figure, blue lines are unit circle and red lines is the tangential line of the point $(0,1)$. We see that the tangential line is vertial when $p = 0.2$ and $p = 0.8$, and is horizontal when $p = 1.2$ and $p = 1.8$. $p = 1$ is the cut-off point. In fact we can do some simple mathematics to prove that the tangential is vertial when $0 \leq p < 1$ and horizontal when $p > 1$, and only when $p = 1$ the tangential is on an angle of 45 degree. Therefore when $0 \leq p < 1$, there is a sharp vertex in $(1,0)$.

Reference:

Davenport, Mark A., et al. "Introduction to compressed sensing." Preprint 93 (2011).