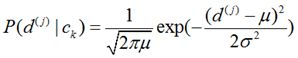朴素贝叶斯与文本分类

0、由乘法公式引出

P(AB) = P(B|A) P(A)

P(B|A) = P(AB) / P(A)

P(B|A) = P(A|B) P(B) / P(A)

 

1、提出问题

对于指定文档从属于某一类别的问题从概率的角度可以理解为 求P(B|A) 意思为给定A的条件，求B发生的概率。那么对于多个类别集合Classify和指定的文档Document，  则有结果类别 Cr = argmax P(Classify | Document)， 求文档Document出现在每一个Classify的概率

 

2、具体化到贝叶斯公式

由P(Document)表示文档, P(Classify)表示分类, 则P(Classify|Document)表示给定Document属于Classify的概率

P(Classify | Document) = P(Document | Classify) P(Classify) / P(Document)

 

P(Classify) ：先验概率

P(Classify | Document) ：后验概率

P(Document | Classify) ：似然函数

P(Document) ：边缘概率

 

3、服从多项式分布的朴素贝叶斯模型

    贝叶斯模型假设文档中的所有特征集合服从二项分布，P(Document | Classify)不能直接求得。一篇文档是由若干个二值特征组成，如果假设每个特征出现的概率是互相独立的。那么一篇文档出现的概率可以认为是所有特征的出现的概率之积。所以把计算P(Document | Classify)转换成计算P(Feature | Classify)

   

    实际是比较任意的文档d_i在每个类别c_j的概率最大，所以P(Document)的概率可以不求出，最终原式变为

   

    朴素贝叶斯模型做文本分类，可以用一袋子词来理解——所有特征集合服从二项分布这个前置约束，既在训练模型时，要知道一篇文档中出现了哪些词（而不是统计每个词在一篇文档出现的次数），特征取值为0或者1(而不是取n)，然后统计该特征(词)在所有样本(文档)出现的计数(而不是次数求和)。

 

4、服从高斯分布的经验贝叶斯估计

使用朴素贝叶斯的前置条件是特征相互独立，但现实往往是数据中的特征与特征之间具有相关性，这需要引入更复杂的模型去估计来表示似然概率 P(Document | Classify)。

根据中心极限定理 —— 同分布或不同分布的随机变量和近似服从高斯正态分布，我们可假设似然函数P(Document | Classify)等于该式

   

其中为期望值，为标准差

实际上我们训练的数据样本集的维数并不为1，假设我们有1000篇已经归类的文档，统计这些文档中出现的词汇数量总计约有10000个，那么就有我们就有1000个样本和10000维度的特征向量所构成的稀疏矩阵，矩阵大小为1000 * 10000。所以上述公式中的d_i需要展开变为{f_1, f_2, ..., f10000}的特征向量，将多个非独立的特征组成的特征向量作为训练模型的输入，会引入协方差矩阵来解决多元问题

 

 

(未完待续)