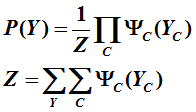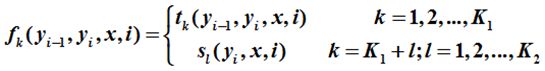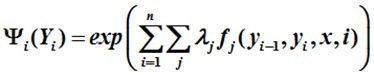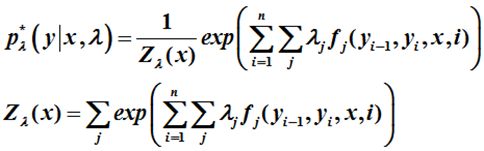条件随机场

1、随机场(RF)

    在概率论中，由样本空间Ω任意取样构成的随机变量X_i的集合S = {X_1,X_2, ..., X_n}，对所有的ω∈Ω式子π(ω) > 0均成立，则称π为一个随机场。

 

2、马尔可夫随机场(MRF)

    当随机变量具有依赖关系时，我们研究随机场才有实际的意义，具有马尔可夫性质的随机变量X_i的全联合概率分布模型，构成马尔可夫随机场。

    马尔可夫随机场对应一个无向图 G = (V, E)。无向图上的每一个节点v ∈ V对应一个随机变量y，俩节点构成的边{u, v} ∈ E 表示节点对应的随机变量y_u, y_v之间有概率依赖关系 P(y_u|y_v)，并且依赖关系服从马尔可夫性——离当前因素比较遥远(这个遥远要根据具体情况自己定义）的因素对当前因素的性质影响不大。因此，MRF的结构本质上反应了我们的先验知识——哪些变量之间有依赖关系需要考虑，而哪些可以忽略。

 

    这样我们可以引入团的概念来定义一组具有依赖关系的随机变量(Y_c)。若无向图G一个节点集合中任意两个结点{u,v}均有连接，则该集合称为团C，若团C不能加入任意节点且同时满足均有连接的约束，则该团称为最大团。

    那么无向图上的联合概率分布P(Y)可写作图中所有最大团C上的函数Y_c的乘积形式，即：

   

其中psai_c(Y_c)称为势函数，它的定义为

   

 

3、条件随机场(CRF)

    如果给定的MRF中每个随机变量y下面还有观察值x，我们要确定的是给定观察集合X下，这个MRF的分布，也就是条件分布，那么这个MRF就称为CRF。它的条件分布形式完全类似于MRF的分布形式，只不过多了一个观察集合X。CRF本质上是给定了观察值 (observations)集合的MRF。

    设G=(V,E)是一个无向图，是以G中节点v为索引的随机变量Y_v构成的集合，在给定X 的条件下，如果每个随机变量Y_v服从马尔可夫属性，即, 则(X,Y)就构成一个条件随机场。注意，定义中并不要求X和Y具有相同结构

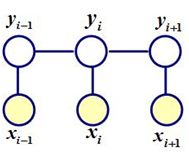
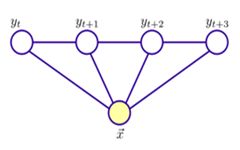
    解决序列标注问题我们可以将条件随机场具体化为线性链结构的条件随机场(Linear-chain CRFs)，其中X表示输入的观测序列，Y表示对应输出的状态序列。

   

   

 

4、形式化

    同最大熵模型相似，我们需要先引入特征函数，其中t_k是定义在边上的转移特征，依赖于当前位置y_i和前一位置y_{i-1}，s_l是定义在节点上的状态特征，只依赖于当前位置。

   

   

    我们可以将转移特征和状态特征用统一的符号表示，则特征函数f(x,y)的数量等于K+L

   

    那么对于每个团Y_i上的势函数psai_i(Y_i)有

   

    带入P(Y|X)与Z(X)最终得到，其中n是随机序列X的个数

   

 

5、与最大熵马尔可夫模型的比较

    对比CRF, MEMM模型公式，可以看出，条件随机场需要计算全局特征向量归一化特征函数的参数向量lambda_i，用以解决MEMM中的标记偏置问题，但很明显这样也会带来的巨大的计算量。