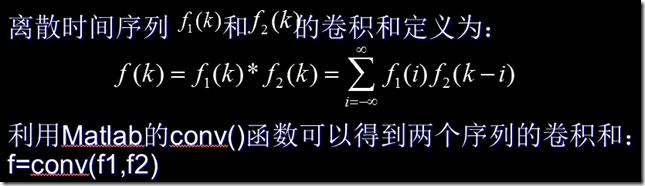MATLAB信号与系统分析（二）——离散时间信号与系统的时域分析

一、离散信号的表示

1、一个离散信号需要用两个向量来表示：

（1）离散信号的幅值

（2）离散信号的位置信息

 

2、用MATLAB实现离散信号的可视化

（1）不能利用符号运算来表示

（2）绘制离散信号一般采用stem命令。

（3）x(n)——stem(n,x)

 

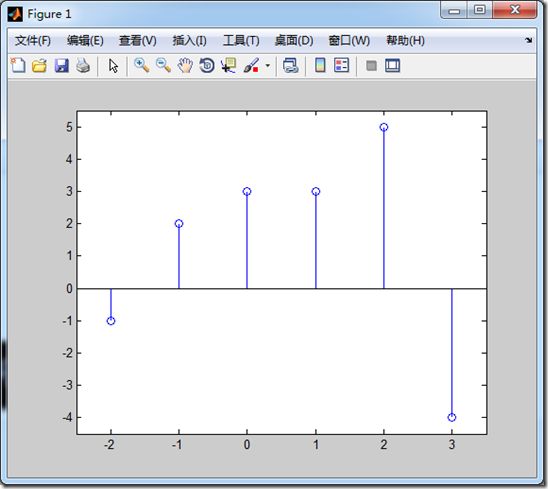
3、一个demo：

clear all;
x=[-1,2,3,3,5,-4];
n=[-2,-1,0,1,2,3];
figure(1)
stem(n,x),axis([-2.5,3.5,-4.5,5.5])

 

二、一些常用的离散信号

1、单位冲激序列的表示

function [x,n] = impseq(k1,k2,k0)

%k1,k2表示序列的起点和终点（只能表示有限序列）

%k0表示冲激点。
n = [k1:k2];
x = [(n-k0) == 0];

 

2、单位阶跃序列的表示：

function [x,n] = stepseq(n1,n2,n0)

%n1,n2表示序列的起点和终点（只能表示有限序列）

n = [n1:n2];
x = [(n-n0) >= 0]

 

三、离散信号的时域运算、时域变换

1、离散序列的相加：

function [y,n] = sigadd(x1,n1,x2,n2)
% implements y(n) = x1(n)+x2(n)
% -----------------------------
% [y,n] = sigadd(x1,n1,x2,n2)
%  y = sum sequence over n, which includes n1 and n2
%  x1 = first sequence over n1
%  x2 = second sequence over n2 (n2 can be different from n1)
%
n = min(min(n1),min(n2)):max(max(n1),max(n2)); % duration of y(n)
y1 = zeros(1,length(n)); y2 = y1;              % initialization
y1(find((n>=min(n1))&(n<=max(n1))==1))=x1;     % x1 with duration of y
y2(find((n>=min(n2))&(n<=max(n2))==1))=x2;     % x2 with duration of y
y = y1+y2;                                     % sequence addition

 

2.离散序列的相乘：

function [y,n] = sigmult(x1,n1,x2,n2)
n = min(min(n1),min(n2)):max(max(n1),max(n2)); 
y1 = zeros(1,length(n)); y2 = y1;            
y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; 
y = y1 .* y2;

 

3、离散序列的反折

function [y,n] = sigfold(x,n)
% implements y(n) = x(-n)
% -----------------------
% [y,n] = sigfold(x,n)
%
y = fliplr(x); n = -fliplr(n);

 

4、离散序列的平移

function [y,n] = sigshift(x,m,n0)
% implements y(n) = x(n-n0)
% -------------------------
% [y,n] = sigshift(x,m,n0)
%
n = m+n0; y = x;

 

5、离散序列的倒相

function [y,n] = sigrev(x,m)
n = m; y =-x;

 

四、离散系统的响应求解

1、零状态、零输入、全响应

 

2、冲激响应、阶跃响应

 

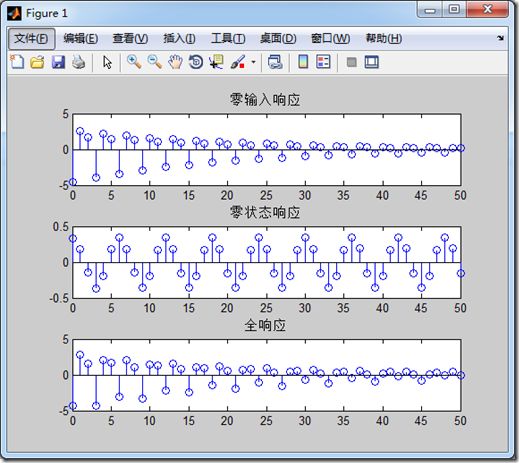
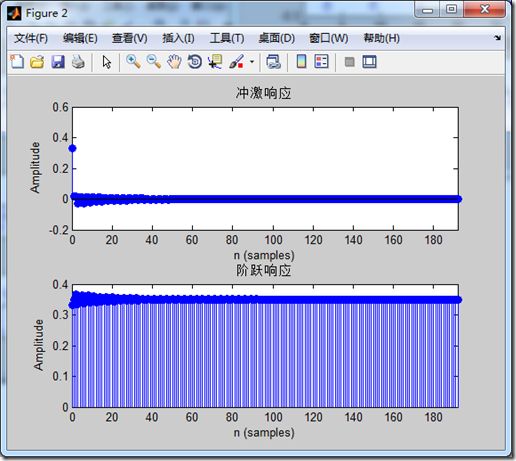
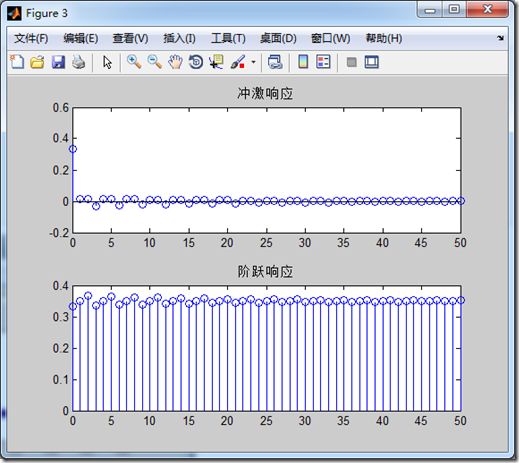
3、一个demo

%ex_6
clear all;
n=0:50;
x=cos(n*pi/3);
a=[1,0.95,0.9025];
b=[1/3,1/3,1/3];
yi=[2,3];
xi=0;
xic=filtic(b,a,yi,xi);
%
y1=filter(b,a,zeros(1,length(n)),xic);
y2=filter(b,a,x);
y3=filter(b,a,x,xic);
figure(1)
subplot(3,1,1),stem(n,y1),title('零输入响应')
subplot(3,1,2),stem(n,y2),title('零状态响应')
subplot(3,1,3),stem(n,y3),title('全响应')
figure(2)
subplot(2,1,1),impz(b,a),title('冲激响应')
subplot(2,1,2),stepz(b,a),title('阶跃响应')
%
u1=impseq(0,50,0);
u2=stepseq(0,50,0);
y4=filter(b,a,u1);
y5=filter(b,a,u2);
n=0:50;
figure(3)
subplot(2,1,1),stem(n,y4),title('冲激响应');
subplot(2,1,2),stem(n,y5),title('阶跃响应');

 

五、离散系统的卷积

function [f,k] = dconv(f1,f2,k1,k2)
    k0= k1(1)+k2(1); 
    k3=length(f1)+length(f2)-2+k0;
    k=k0:k3;
    f = conv(f1,f2);