旋转卡壳算法及应用 (参考论文）
多看论文开眼界！
转自：http://blog.csdn.net/acmaker/article/details/3188177
一、目录
一些历史：
1978年， M.I. Shamos's Ph.D. 的论文"Computational Geometry"标志着计算机科学的这一领域的诞生。 当时他发表成果的是一个寻找凸多边形直径的一个非常简单的算法， 即根据多边形的一对点距离的最大值来确定。后来直径演化为由一对对踵点对来确定。 Shamos提出了一个简单的 O(n) 时间的算法来确定一个凸 n 角形的对踵点对。 因为他们最多只有 3n/2 对， 直径可以在 O(n) 时间内算出。
如同Toussaint后来提出的， Shamos的算法就像绕着多边形旋转一对卡壳。 因此就有了术语“旋转卡壳”。 1983年， Toussaint发表了一篇论文， 其中用同样的技术来解决许多问题。 从此， 基于此模型的新算法就确立了， 解决了许多问题。
他们包括：
- 计算距离
- 凸多边形直径
- 凸多边形宽
- 凸多边形间最大距离
- 凸多边形间最小距离
- 外接矩形
- 最小面积外接矩形
- 最小周长外接矩形
- 三角剖分
- 洋葱三角剖分
- 螺旋三角剖分
- 四边形剖分
- 凸多边形属性
- 合并凸包
- 找共切线
- 凸多边形交
- 临界切线
- 凸多边形矢量和
- 最薄截面
- 最薄横截带
二、计算距离
1.凸多边形直径
我们将一个多边形上任意两点间的距离的最大值定义为多边形的直径。 确定这个直径的点对数可能多于一对。 事实上， 对于拥有 n 个顶点的多边形， 就可能有 n 对“直径点对”存在。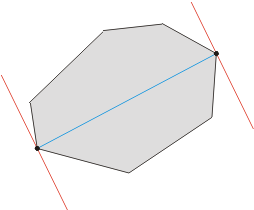
一个多边形直径的简单例子如左图所示。 直径点对在图中显示为被平行线穿过的黑点 （红色的一对平行线）. 直径用浅蓝色高亮显示。
显然， 确定一个凸多边形 P 直径的点对不可能在多边形 P 内部。 故搜索应该在边界上进行。 事实上， 由于直径是由多边形的平行切线的最远距离决定的， 所以我们只需要查询对踵点。 Shamos (1978) 提供了一个 O(n) 时间复杂度计算n点凸包对踵点对的算法。直径通过遍历顶点列表， 得到最大距离即可。 如下是1985年发表于 Preparata 和 Shamos 文章中的 Shamos 算法的伪代码。
输入是一个多边形 P={p1,...,pn}.
begin
p0:=pn;
q:=NEXT[p];
while (Area(p,NEXT[p],NEXT[q]) > Area(p,NEXT[p],q)) do
q:=NEXT[q];
q0:=q;
while (q != p0) do
begin
p:=NEXT[p];
Print(p,q);
while (Area(p,NEXT[p],NEXT[q]) > Area(p,NEXT[p],q) do
begin
q:=NEXT[q];
if ((p,q) != (q0,p0)) then Print(p,q)
else return
end;
if (Area(p,NEXT[p],NEXT[q]) = Area(p,NEXT[p],q)) then
if ((p,q) != (q0,p0)) then Print(p,NEXT[q])
else Print(NEXT[p],q)
end
end.
此处
Print(p,q) 表示将 (p,q) 作为一个对踵点对输出，
Area(p,q,r) 表示三角形 pqr 的有向面积。
虽然直观上看这个过程与常规旋转卡壳算法不同， 但他们在本质上是相同的， 并且避免了所有角度的计算。
如下是一个更直观的算法：
- 计算多边形 y 方向上的端点。 我们称之为 ymin 和 ymax 。
- 通过 ymin 和 ymax 构造两条水平切线。 由于他们已经是一对对踵点， 计算他们之间的距离并维护为一个当前最大值。
- 同时旋转两条线直到其中一条与多边形的一条边重合。
- 一个新的对踵点对此时产生。 计算新的距离， 并和当前最大值比较， 大于当前最大值则更新。
- 重复步骤3和步骤4的过程直到再次产生对踵点对 (ymin,ymax) 。
- 输出确定最大直径的对踵点对。
2. 凸多边形的宽度
我们假设存在一个线段 [a,b]， 以及两条通过 a 和 b 的平行线。 通过绕着这两个点旋转这两条线， 使他们之间的距离递增或递减。 特别的， 总存在一个 特定旋转方向 使得两条线之间的距离通过旋转变小。
这个简单的结论可以被应用于宽度的问题中： 不是所有的方向都需要考虑。 假设给定一个多边形， 同时还有两条平行切线。 如果他们都未与边重合， 那么我们总能通过旋转来减小他们之间的距离。 因此， 两条平行切线只有在其中至少一条与边重合的情况下才可能确定多边形的宽度。
这就意味着“对踵点 点-边”以及“边-边”对需要在计算宽度过程中被考虑。
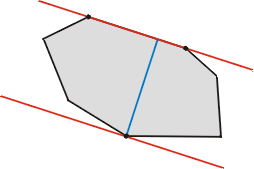
一个凸多边形宽度的示意图。 直径对如图由平行切线（红线）穿过的黑点所示。 直径如高亮的淡蓝色线所示。
一个与计算直径问题非常相似的算法可以通过遍历多边形对踵点对列表得到， 确定顶点-边以及边-边对来计算宽度。 选择过程如下:
- 计算多边形 y 方向上的端点。 我们称之为 ymin 和 ymax。
- 通过 ymin 和 ymax 构造两条水平切线。如果一条（或者两条）线与边重合， 那么一个“对踵点 点-边”对或者“边-边”对已经确立了。 此时， 计算两线间的距离， 并且存为当前最小距离。
- 同时旋转两条线直到其中一条与多边形的一条边重合。
- 一个新的“对踵点 点-边”对（或者当两条线都与边重合，“边-边”对）此时产生。 计算新的距离， 并和当前最小值比较， 小于当前最小值则更新。
- 重复步骤3和步骤4（卡壳）的过程直到再次达到最初平行边的位置。
- 将获得的最小值的对作为确定宽度的对输出。
更为直观的算法再次因为需要引进角度的计算而体现出其不足。 然而， 就如在凸多边形间最大距离问题中一样， 有时候更为简单、直观的旋转卡壳算法必须被引入计算。
3.凸多边形间最大距离
给定两个凸多边形 P 和 Q， 目标是需要找到点对 (p,q) （p 属于 P 且 q 属于 Q） 使得他们之间的距离最大。
很直观地，这些点不可能属于他们各自多边形的内部。 这个条件事实上与直径问题非常相似：
两凸多边形 P 和 Q 间最大距离由多边形间的对踵点对确定。
虽然说法一样， 但是这个定义与给定凸多边形的对踵点对的不同。
与凸多边形间的对踵点对本质上的区别在于切线是有向且反向的。 下图展示了一个例子：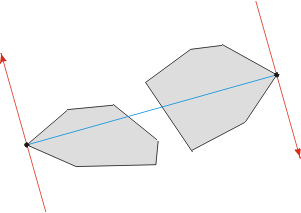 
上述结论暗示不单纯只是顶点对需要检测， 而仅仅是特定的顶点对需要被考虑到。 事实上他们只检测一个基于旋转卡壳模式的算法确立的平行切线。
考虑如下的算法， 算法的输入是两个分别有 m 和 n 个顺时针给定顶点的凸多边形 P 和 Q。
- 计算 P 上 y 坐标值最小的顶点（称为 yminP ） 和 Q 上 y 坐标值最大的顶点（称为 ymaxQ）。
- 为多边形在 yminP 和 ymaxQ 处构造两条切线 LP 和 LQ 使得他们对应的多边形位于他们的右侧。 此时 LP和 LQ 拥有不同的方向， 并且 yminP 和 ymaxQ 成为了多边形间的一个对踵点对。
- 计算距离(yminP,ymaxQ) 并且将其维护为当前最大值。
- 顺时针同时旋转平行线直到其中一个与其所在的多边形的边重合。
- 一个新的对踵点对产生了。 计算新距离， 与当前最大值比较， 如果大于当前最大值则更新。 如果两条线同时与边发生重合， 此时总共三个对踵点对（先前顶点和新顶点的组合）需要考虑在内。
- 重复执行步骤4和步骤5， 直到新的点对为(yminP,ymaxQ)。
- 输出最大距离。
旋转卡壳模式确保了所有的对踵点对都被考虑到。 此外， 整个算法拥有线性的时间复杂度， 因为（除了初始化）， 执行步数与顶点数相同。
类似的算法可以被用于凸多边形间最小距离问题中。
4.凸多边形间最小距离
给定两个非连接（比如不相交）的凸多边形 P 和 Q， 目标是找到拥有最小距离的点对 (p,q) （p 属于 P 且 q 属于Q）。事实上， 多边形非连接十分重要， 因为我们所说的多边形包含其内部。 如果多边形相交， 那么最小距离就变得没有意义了。 然而， 这个问题的另一个版本， 凸多边形顶点对间最小距离对于相交和非相交的情况都有解存在。
回到我们的主问题： 直观的， 确定最小距离的点不可能包含在多边形的内部。 与最大距离问题相似， 我们有如下结论：
两个凸多边形 P 和 Q 之间的最小距离由多边形间的对踵点对确立。 存在凸多边形间的三种多边形间的对踵点对， 因此就有三种可能存在的最小距离模式：
- “顶点-顶点”的情况
- “顶点-边”的情况
- “边-边”的情况
换句话说， 确定最小距离的点对不一定必须是顶点。 下面的三个图例表明了以上结论：
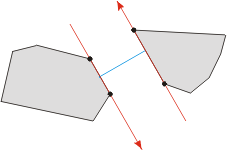
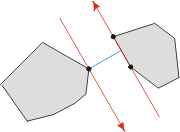
给定结果， 一个基于旋转卡壳的算法自然而然的产生了:
考虑如下的算法， 算法的输入是两个分别有 m 和 n 个顺时针给定顶点的凸多边形 P 和 Q。
- 计算 P 上 y 坐标值最小的顶点（称为 yminP ） 和 Q 上 y 坐标值最大的顶点（称为 ymaxQ）。
- 为多边形在 yminP 和 ymaxQ 处构造两条切线 LP 和 LQ 使得他们对应的多边形位于他们的右侧。 此时 LP和 LQ 拥有不同的方向， 并且 yminP 和 ymaxQ 成为了多边形间的一个对踵点对。
- 计算距离(yminP,ymaxQ) 并且将其维护为当前最小值。
- 顺时针同时旋转平行线直到其中一个与其所在的多边形的边重合。
- 如果只有一条线与边重合， 那么只需要计算“顶点-边”对踵点对和“顶点-顶点”对踵点对距离。 都将他们与当前最小值比较， 如果小于当前最小值则进行替换更新。 如果两条切线都与边重合， 那么情况就更加复杂了。 如果边“交叠”， 也就是可以构造一条与两条边都相交的公垂线（但不是在顶点处相交）， 那么就计算“边-边”距离。 否则计算三个新的“顶点-顶点”对踵点对距离。 所有的这些距离都与当前最小值进行比较， 若小于当前最小值则更新替换。
- 重复执行步骤4和步骤5， 直到新的点对为(yminP,ymaxQ)。
- 输出最大距离。
最小距离和最大距离的问题表明了旋转卡壳模型可以用在不同的条件下（与先前的直径和宽度问题比较）。 这个模型可以应用于两个多边形的问题中。
“最小盒子”问题（最小面积外接矩形）通过同一多边形上两个正交切线集合展示了另一种条件下旋转卡壳的应用。
三、外接矩形
1.凸多边形最小面积外接矩形
给定一个凸多边形 P ， 面积最小的能装下 P （就外围而言）的矩形是怎样的呢？ 从技术上说， 给定一个方向， 能计算出 P 的端点并且构由此造出外接矩形。 但是我们需要测试每个情形来获得每个矩形来计算最小面积吗？ 谢天谢地， 我们不必那么干。
对于多边形 P 的一个外接矩形存在一条边与原多边形的边共线。
上述结论有力地限制了矩形的可能范围。 我们不仅不必去检测所有可能的方向， 而且只需要检测与多边形边数相等数量的矩形。
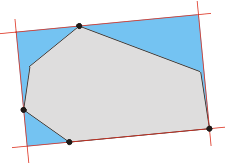图示上述结论： 四条切线（红色）， 其中一条与多边形一条边重合， 确定了外接矩形（蓝色）。
一个简单的算法是依次将每条边作为与矩形重合的边进行计算。 但是这种构造矩形的方法涉及到计算多边形每条边端点， 一个花费 O(n) 时间（因为有 n 条边）的计算。 整个算法将有二次时间复杂度。
一个更高效的算法已经发现。 利用旋转卡壳， 我们可以在常数时间内实时更新， 而不是重新计算端点。
实际上， 考虑一个凸多边形， 拥有两对和 x 和 y 方向上四个端点相切的切线。 四条线已经确定了一个多边形的外接矩形。 但是除非多边形有一条水平的或是垂直的边， 这个矩形的面积就不能算入最小面积中。
然而， 可以通过旋转线直到条件满足。 这个过程是下属算法的核心。 假设按照顺时针顺序输入一个凸多边形的n 个顶点。
- 计算全部四个多边形的端点， 称之为 xminP， xmaxP， yminP， ymaxP。
- 通过四个点构造 P 的四条切线。 他们确定了两个“卡壳”集合。
- 如果一条（或两条）线与一条边重合， 那么计算由四条线决定的矩形的面积， 并且保存为当前最小值。 否则将当前最小值定义为无穷大。
- 顺时针旋转线直到其中一条和多边形的一条边重合。
- 计算新矩形的面积， 并且和当前最小值比较。 如果小于当前最小值则更新， 并保存确定最小值的矩形信息。
- 重复步骤4和步骤5， 直到线旋转过的角度大于90度。
- 输出外接矩形的最小面积。
因为两对的“卡壳”确定了一个外接矩形， 这个算法考虑到了所有可能算出最小面积的矩形。 进一步， 除了初始值外， 算法的主循环只需要执行顶点总数多次。 因此算法是线性时间复杂度的。
一个相似但是鲜为人知的问题是最小周长外接矩形问题。 有趣的是这两个问题是完全不同的问题， 因为存在（尽管极少）最小面积外接矩形和最小周长外接矩形多边形不重合的多边形。
2.凸多边形最小周长外接矩形
这个问题和最小面积外接矩形相似。 我们的目标是找到一个最小盒子（就周长而言）外接多边形 P 。
有趣的是通常情况下最小面积的和最小周长的外接矩形是重合的。 有人不禁想问这是不是总成立的。 下面的例子回答了这个问题： 多边形（灰色的）及其最小面积外接矩形（左边的）和最小周长外接矩形（右边的）。
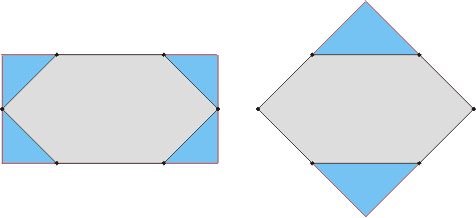
现在， 给定一个方向， 我们可以算出 P 的端点， 以此来确定一个外接矩形。 但是， 就如同面积问题中一样， 由于有下面的结论， 我们不必检测每个状态来获得拥有最小周长的矩形：
凸多边形 P 的最小周长外接矩形存在一条边和多边形的一条边重合。
这个结论通过枚举多边形的一条重合边有力地限制了矩形的可能范围。 
图示上述结论： 四条切线（红色）， 其中一条与多边形边重合， 确定了外接矩形（蓝色）。
因为与其面积问题相当， 这个问题可以通过一个基于旋转卡壳的相似的算法来解决。
下属算法的输入是顺时针顺序给定的一个凸多边形的 n 个顶点。
- 计算全部四个多边形的端点， 称之为 xminP， xmaxP， yminP， ymaxP。
- 通过四个点构造 P 的四条切线。 他们确定了两个“卡壳”集合。
- 如果一条（或两条）线与一条边重合， 那么计算由四条线决定的矩形的面积， 并且保存为当前最小值。 否则将当前最小值定义为无穷大。
- 顺时针旋转线直到其中一条和多边形的一条边重合。
- 计算新矩形的周长， 并且和当前最小值比较。 如果小于当前最小值则更新， 并保存确定最小值的矩形信息。
- 重复步骤4和步骤5， 直到线旋转过的角度大于90度。
- 输出外接矩形的最小周长。
因为两对的“卡壳”确定了一个外接矩形， 这个算法考虑到了所有可能算出最小周长的矩形。 进一步， 除了初始值外， 算法的主循环只需要执行顶点总数多次。 因此算法是线性时间复杂度的。
问题处理同样包含三角形。 有两个特例， 具体参见洋葱三角剖分和螺旋三角剖分。
四、三角剖分
1.洋葱三角剖分
给定一个平面上的点集， 目标是构造一个点集的三角剖分。
从Lennes 1911年二次时间复杂度的源算法到Chazelle 1991线性时间复杂度的算法， 前人已经做了许多关于提高三角剖分算法效率的研究。
这里的焦点是关于一种特殊的三角剖分， 一种基于对点集进行“剥洋葱皮”操作。
考虑平面上一个有 n 个点的集合 S 。 计算 S 的凸包， 并且设 S' 为在凸包内的点集。 然后计算 S' 的凸包并且反复执行这个操作直到没有点剩下。 最后剩下了一个像鸟巢一样层层覆盖的凸包序列， 称为洋葱皮集合 S 。 感谢Chazelle的算法， 这个结构能够在 O(n log n) 时间操作内实现。
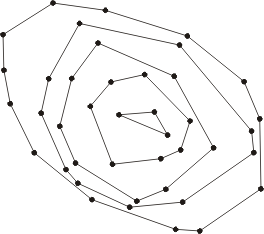一个点集的洋葱皮。 注意除了凸多边形外， 最里面的结构可能是一条线段或者是一个单一点。 这个图给出了点的层次信息， 比如点间哪个相对更“深”。
两个嵌套的凸包间的区域称为一个环面。 Toussaint在1986年发表了一个利用旋转卡壳计算环面三角剖分的简单算法。 利用这个方法， 一旦构造出洋葱皮， 就能在现行时间内构造出三角剖分。 进一步， 这个三角剖分有两个特点： 他的子图仍然是洋葱皮， 并且他是一个哈密尔顿图， 即三角剖分图的顶点可以是链状的。
一个环面的三角剖分算法是非常简单的。 算法输入一个被凸包 P 包裹的凸包 Q， 他们的顶点都是顺时针序的。
- 将凸包的边作为三角剖分的边插入。
- 计算 P 和 Q 的 x 坐标最小的点， 分别称为 xmin(P) 和 xmin(Q) 。
- 在 xmin(P) 和 xmin(Q) 处构造两条铅垂切线， 称之为 LP 和 LQ 。
- 将 (xmin(P), xmin(Q)) 作为三角剖分的一条边插入。
- 当前 LP 和 LQ 对应的 p 和 q 点分别是 xmin(P) 和 xmin(Q)。
- 将线顺时针旋转直到其中一个与一条边重合。 一个新的顶点由此被一条线“击”出。
- 如果他属于 P （称为 p'）， 插入 (p', q) 到三角剖分中。 更新当前的点为 p' 和 p' 。
- 如果他属于 Q （称为 q'）， 插入 (p, q') 到三角剖分中。 更新当前的点为 p 和 q' 。
- 对于平行边的情况， 两条切线都和边重合， 并且两个新的顶点被“击”出（称他们为 p' 和 q'）。 然后插入 (p', q') ， 以及 (p, q') 和 (p', q) 到三角剖分中。 更新当前的点为 p' 和 q' 。
- 重复执行上述步骤直到达到开始的最小点。
一个换面的三角剖分如下所示：
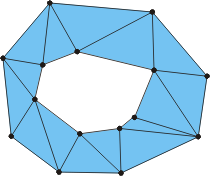
上述的算法拥有线性时间复杂度。 当对于一个点集进行三角剖分的时候， 一个凸包在整个过程中遍历（最多）两次， 最里面和最外部的凸包都只执行遍历一次。 因此对于一个 n 个点的三角剖分的总运行时间是 O(n) 。
另一个有效且与三角剖分有关的问题是基于点集的凸螺旋线的螺旋三角剖分。
2.螺旋三角剖分
点集的螺旋三角剖分是基于集合螺旋凸包的三角剖分图。
凸螺旋线可以通过如下方法构造：
- 从一个特定的端点开始（比如给定方向上的最小点）， 这里取有最小 x 坐标的点。
- 通过那个点构造一条铅垂线。
- 按照一个给定的方向旋转线（总保持顺时针或者是逆时针方向）， 直到线“击” 出另一个顶点。
- 将两个点用一条线段连接。
- 重复步骤3和步骤4， 但是总忽略已经击出的点。
大体上， 这个过程类似于计算凸包的卷包裹算法， 但是不同在于其循环永远不会停止。 对于一个凸包上有 h 个点的点集， 存在 2h 个凸螺旋线： 对于每个起点有顺时针和逆时针螺旋线两种。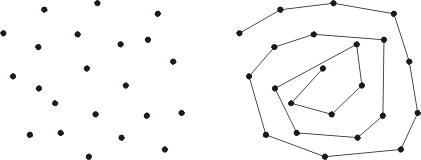 
一个点集（左边）， 及其顺时针凸螺旋线， 以最小的 x 坐标点作为初始点。
有趣的是， 一个点集的凸螺旋线和洋葱皮可以在线性时间内相互转换。 进一步的， 类似于洋葱三角剖分， 我们可以定义一个点集的子图为凸螺旋线的螺旋三角剖分。
构造螺旋三角剖分的算法， 虽然是基于环面三角剖分的， 但是却更为复杂， 因为螺旋线必须被分割为合适的凸包链。 假设输入是一个点集的顺时针凸螺旋线 C ， 且有 C = { p1 , ... , pn } 。
- 将凸螺旋线的边作为三角剖分的边插入。
- 从 p1 开始， 寻找点集凸螺旋线上的最后一个点 ph 。
- 延长凸螺旋线上的最后一条边 [p(n-1),pn] 直到其与凸螺旋线相交。 标记交点为 q' 。
- 构造与 C 切于点 q' 的切线。 逆时针旋转那条线直到他与 C 相交于一点 q 并且平行于 [p(n-1),pn] 。
- 将 [p(n-1),q] 插入三角剖分中。
- 此操作后将凸螺旋链分割称了两个部分： 链外的部分和链内的多边形区域。 设 Co = { p1 , ... , q } 且 Ci = { ph , ... , q , ... , pn } 。 这个构造过程如下图所示：
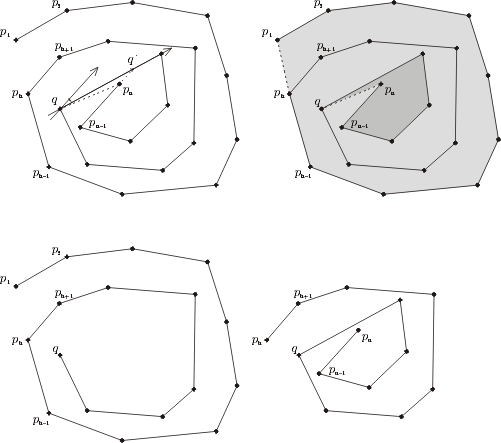左上角： 构造过程。 右上角： 螺旋外和内部的多边形区域。 底部： 外部和内部的凸链 Co 和Ci 。 - 外部螺旋区域可以如环面一样进行三角剖分。 Co 和 Ci 此时可以被看成一个嵌套凸包。
- 内部的多边形区域可以很容易的在 pn 处星型划分形成三角剖分。
- 这两个三角剖分的组合构成了整个螺旋三角剖分的结构。
一个螺旋凸包的例子和其三角剖分如下所示：
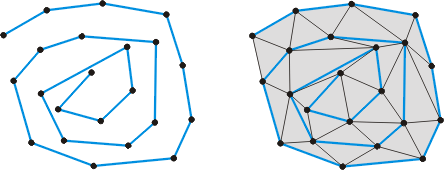
上述的算法是线性时间复杂度的， 算法的时间依赖于环面剖分的运行时间。
3.四边形剖分
虽然三角剖分是一个更常用的结构， 但最近四边形剖分在某些特定条件下显得更适用， 比如 scattered data interpolation 以及 finite element method 等。
一个四边形剖分实际上是一个点集的四边形分割。 一些与三角剖分本质上的区别（除了特别明显的）应该引起注意：
首先， 不是所有的点集都存在四边形剖分。 事实上， 只有偶数点集才有。 对于奇数点集， 有时需要附加点（称为Steiner点）到原集合中， 从而构造一个四边形剖分。
同时， 人们经常期望四边形剖分构造拥有一些“好的”性质， 比如凸的。 这个与三角剖分是不同的。
有许多简单的四边形剖分算法。 比如， 首先考虑点集的三角剖分， 然后加入一个Steiner点到每个三角形内部， 以及每条边的中间。 连接这些新点构成了四边形剖分（这是DeBerg提出的）。
Bose 和 Toussaint 在1997年提出从一个点集的螺旋三角剖分开始， 来构造一个o四边形剖分。
如果点集是偶数的， 那么每隔一个的对角线（在螺旋三角剖分算法中加入的）移除， 构造了一个四边形剖分。 如果是奇数个点， 那么从最后一条对角线开始每个隔一条对角线（比如最后一个， 倒数第三个等）进行移除， 在被移除的第一条对角线附近加入一个Steiner点。 下图展示第一种情况（偶数个点的点集）。 螺旋三角剖分（左边）， 和最终的四边形剖分（右边）。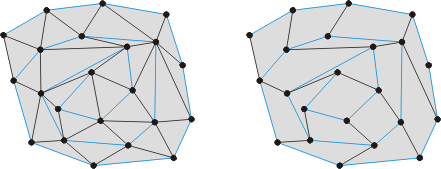 
因为对角线的移除过程（和必要的更新）花费 O(n) 的时间， 这个四边形剖分算法与螺旋三角剖分有相同的时间复杂度。 这个算法的优点在于便于理解与实现（一旦凸螺旋线建立）， 并且事实上其产生了一个比许多竞争者“更好的”四边形剖分算法。
下一个问题集是关于凸多边形， 特别的， 关于凸包上的操作， 比如合并凸包。
五、凸多边形属性
1.合并凸包
考虑如下问题： 给定两个凸多边形， 包含他们并的最小凸多边形是怎样的？ 答案即合并凸包后得到的凸多边形。合并凸包可以通过一个低效的方式实现： 给定两个多边形的所有顶点， 计算这些点对应的凸包。 更高效的方法是存在的， 他依赖于多边形间的 桥 的查找。 下图描述了这个概念：
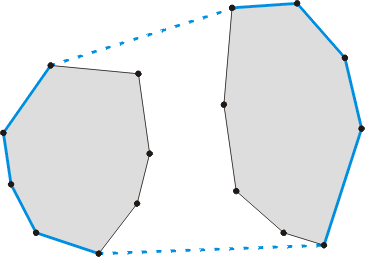两个不相交的凸多边形。 合并后的凸包包含两个多边形中的凸包链（途中蓝色粗实线）， 通过多边形间的桥进行连接（途中蓝色虚线）
给定两个不相交的多边形， 在多边形间存在两条桥。 多边形相交时， 拥有和顶点数同样数量的桥， 如下图所示：
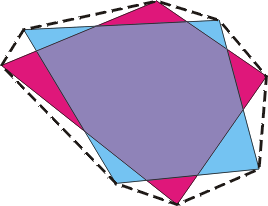两个相交的凸多边形。 合并凸包只包含多边形间的桥（图中虚线所示）。 存在连接八个顶点的八个桥。
合并操作的核心是分治方法。 他同样用于多边形中。 一个获取凸包的十分简单的方法是将点集分为两部分， 分别计算两个较小点集的凸包， 并且将他们合并。 每个集合再次被分割， 直到元素的个数足够小（比如说三个或者更少） 因此凸包就能被很容易获得了。
Toussaint 提出利用旋转卡壳来寻找两个凸多边形间的桥。 这个方法的主要优点在于其利用回溯， 并且多边形可以交叠（其他的算法要求多边形不相交）。 下述结论是他的算法的主要过程：
给定凸多边形 P = { p(1) , ... , p(m) } 和 Q = { q(1) , ... , q(n) }，一个点对 (p(i), q(j)) 形成 P 和 Q 之间的桥当且仅当：
- (p(i), q(j)) 形成一个并踵点对。
- p(i-1), p(i+1), q(j-1), q(j+1) 都位于由 (p(i), q(j)) 组成的线的同一侧。
- 分别计算 P 和 Q 拥有最大 y 坐标的顶点。 如果存在不止一个这样的点， 取 x 坐标最大的。
- 构造这些点的遂平切线， 以多边形处于其右侧为正方向（因此他们指向 x 轴正方向）。
- 同时顺时针旋转两条切线直到其中一条与边相交。 得到一个新的并踵点对 (p(i), q(j)) 。 对于平行边的情况， 得到三个并踵点对。
- 对于所有有效的并踵点对 (p(i), q(j))： 判定 p(i-1), p(i+1), q(j-1), q(j+1) 是否都位于连接点 (p(i), q(j)) 形成的线的同一侧。 如果是， 这个并踵点对就形成了一个桥， 并标记他。
- 重复执行步骤3和步骤4直到切线回到他们原来的位置。
- 所有可能的桥此时都已经确定了。 通过连续连接桥间对应的凸包链来构造合并凸包。
一个凸多边形间的桥实际上确定了另一个有用的概念：多边形间公切线。 同时， 桥也是计算凸多边形交的算法核心。
2.找共切线
公切线是同时与多边形相切的简单直线， 并且两个多边形都位于线的同一侧。 换句话说， 一条公切线是一条与两个多边形都相切的线。 一个例子如下图所示：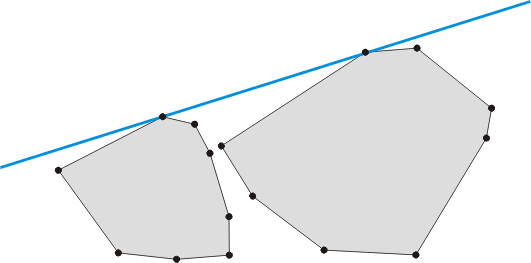
两个不相交的凸多边形和一条他们的公切线
事实上， 公切线可以通过多边形间的一些确定桥的点对来确立。 因此， 给定两个不相交的多边形， 就存在两个多边形间两条公切线， 并且当多边形相交时， 还有可能存在与顶点数一样多的公切线。
用来计算两多边形间桥的算法（如归并算法）同样可以用来确定公切线。
另一个“版本”的两多边形的公切线是关键切线。 那种情况下多边形分立于线的两侧。
桥可以用来计算多边形的交。
3.凸多边形交
给定两个多边形， 我们第一个需要讨论的问题应该是：“他们相交吗？”。 Chazelle 和 Dobkin 1980年在他们的一篇叫做“Detection is easier than computation”的论文中发表了一个对数时间级的算法（论文的名字很贴切）。 对于多边形的交， 许多算法能计算出交集。 有趣的是一个结论（由Guibas提出）证明了多边形交点和和他们之间的桥是一一对应关系。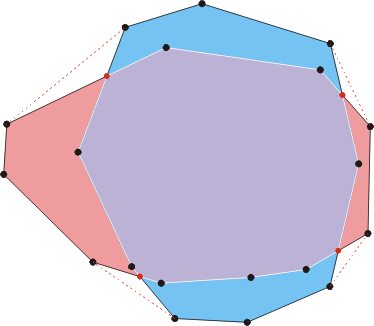
两个多边形（浅红色和蓝色）和他们的交集（浅紫色）。 交点以红色标记。 每个交点与一个多边形之间的桥（标记为红色点划线）有关。
Toussaint在1985年的文献中利用Guibas的结论， 加上他先前的关于查找桥的算法来计算交点集。 他的算法利用桥来计算交点集。 一旦他们被找到， 与合并凸包的操作类似， 凸链以及交点集形成了多边形的交集。
算法的细节， 特别是从桥到交点的计算可以在Toussaint的论文中找到：
G.T. Toussaint. A simple linear algorithm for intersecting convex polygons. The Visual Computer. 1: 118-123. 1985.
下一个问题设计寻找两个凸多边形的临界切线。
4.临界切线
两个凸多边形间的临界切线（一般被叫做CS线）是使得两个多边形分居线不同侧的切线。 换句话说， 他们分隔了多边形。CS线可以应用于motion planning， visibility 和 range fitting。
下图是关于两个多边形和他们的两条临界切线。
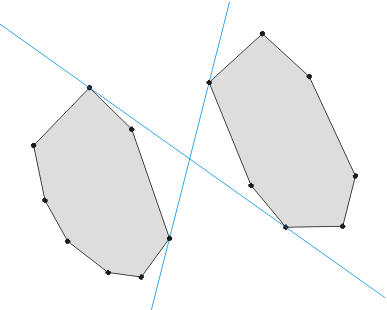
这里要注意的一点是假设数据是以标准形式给出的， CS线只会在两个顶点处与两个多边形相交。 因此， 一条CS线由多边形间顶点对确定。
如下的结论描述了这个点对：
给定两个凸多边形 P， Q， 两个顶点 p(i), q(j) （分别属于 P 和 Q） 确定一条CS线当且仅当：
- p(i), q(j) 构成多边形间对踵点对。
- p(i-1),p(i+1) 位于线 (p(i), q(j)) 一侧，同时q(j-1),q(j+1) 位于另一次。
- 计算 P 上 y 坐标值最小的顶点（称为 yminP ） 和 Q 上 y 坐标值最大的顶点（称为 ymaxQ）。
- 为多边形在 yminP 和 ymaxQ 处构造两条切线 LP 和 LQ 使得他们对应的多边形位于他们的右侧。 此时 LP 和 LQ拥有不同的方向， 并且 yminP 和 ymaxQ 成为了多边形间的一个对踵点对。
- 令 p(i)= yminP， q(j)= ymaxQ。 (p(i), q(j)) 构成了多边形间的一个对踵点对。 检测是否有 p(i-1),p(i+1) 在线 (p(i),q(j)) 的一侧， 并且 q(j-1),q(j+1) 在另一侧。 如果成立， (p(i), q(j)) 确定了一条CS线。
- 旋转这两条线， 直到其中一条和其对应的多边形的边重合。
- 一个新的对踵点对确定了。 如果两条线都与边重合， 总共三对对踵点对（原先的顶点和新的顶点的组合）需要考虑。 对于所有的对踵点对， 执行上面的测试。
- 重复执行步骤4和步骤5， 直到新的点对为(yminP,ymaxQ)。
- 输出CS线。
这个算法基本通过绕着多边形旋转切线， 顺序查找所有多边形间的对踵点对。 每次一对对踵点确定后， 执行所有必要的测试。 在上述过程执行完后， 所有的临界切线都被找到了。
算法的运行时间由步骤1和步骤6决定， 他们都花费 O(n) 的时间（所有的检测都花费常数时间。 因为有 O(n) 的对踵点对， 总的花费为 O(n)）。
关于凸多边形的学习， 最后的操作是凸多边形矢量和。
5.凸多边形矢量和
给定平面上两个凸多边形 P 和 Q ， P 和 Q 的矢量和， 记为 P + Q 定义如下：多边形矢量和在 motion planning 中也称为 Minkowski 总数。
考虑上述的定义， 许多问题可以通过询问集合 P + Q 的组成， 他拥有的性质等等。 下属结果帮助我们描述多边形矢量和。
- P + Q 是一个凸多边形。
- 顶点集 P + Q 是顶点集 P 和 Q 的和。
- 顶点集 P + Q 是 P 和 Q 间的并踵点对集。
- 给定分别有 m 和 n 个顶点的 P 和 Q ， P + Q 有不多于 m + n 个顶点。
最后， 下属结论不仅仅描述了这个问题， 同时也提供了一个一个个顶点的增量式计算矢量和的计算方法。
给定 P + Q 集合的第 k 个向量 z(k)， 满足 z(k) = p(i) + q(j)。 构造在 p(i) 和 q(j) 处构造两条平行切线， 使得多边形同时位于各自线的右侧。 两条线分别在 p(i) 和 q(j) 处确定了角 theta(i) 和 phi(j) （如下图所示）
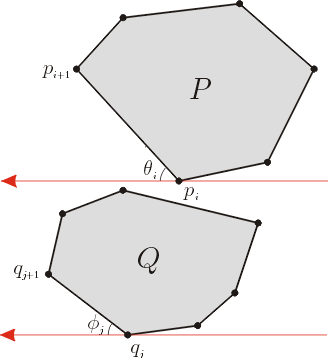
因此下一个向量 z(k+1) 等于：
- p(i+1) + q(j) 若 theta(i) < phi(j)
- p(i) + q(j+1) 若 theta(i) > phi(j)
- p(i+1) + q(j+1) 若 theta(i) = phi(j)
下述的多边形和他们的矢量和作为一个例子。
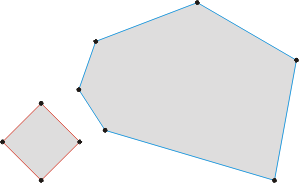
两个凸多边形。 第一个多边形的边用红色标记， 第二个用蓝色。
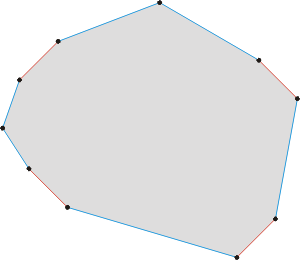
上述多边形的矢量和。 其边的颜色与原多边形的一致。
用上述的结果， 我们十分容易的就能构造出一个算法来计算矢量和。 第一个向量可以是在给定方向上边界向量的和（如 y 轴负方向）。 切线构造后， 在计算角度时候更新， 下一个点就很明确了。 我们需要做的只是同时旋转两条线到新的位置来确定新的角度。
算法的正确性来自主要的结论； 他是线性时间复杂度的， 因为每一步只有一个所要求的向量和集合中的向量被确定， 并且他们只有 m + n 个， 因此总运行时间是 m + n 。
六、最薄截面
1.最薄横截带
考虑下述设备放置问题：一个“消费群体群”的集合是以个体呈现为平面上凸多边形的一个家庭 F 给出的。 我们的目标是找到一个“设备”， 一条平面上的直线， 使得线到消费者的最大距离最小。最后一点需要澄清。 直线与任何一个多边形的距离都是指多边形上一点到线的正交距离的最小值。 因此，每个多边形到线的距离是唯一的。
现在， 给定家庭中各个呈多边形的成员和平面上的一条直线， 每个多边形都有一个到线的距离。 因此， 对于整个家庭存在一个最大的线-多边形距离。 这个距离同时依赖于线与各个家庭成员多边形。
这个问题的目标是： 给定一个特定的家庭成员多边形集， 找到使得这个最大距离最小的线。 这个问题同样存在着其他版本， 常见的有找一条线使得距离和最小， 或是使得多边形带权距离和最小。
这里的提出的结论是Robert和Toussaint在1990年发表的。
主问题等价于找到一个宽最小的带（一个平面上由两条平行线为边界的区域）和所有的家庭成员多边形相交。因此， 带的中心（与带的边界线平行等距的线）就是所求的使得最大距离最小的线。
为了讨论这个问题我们做如下定义：
平面上的一条直线 l ， 其方程为 ax + by + c = 0 （且 b > 0 或 a = -1）将平面分为两个区域：上半平面 Hu(l) 中的点 p = (px,py) 满足 apx + apy + c >= 0 ， 且下半平面 Hl(l) 中的点 p = (px,py) 满足 apx + apy + c <= 0 。
通过上面的定义， 如果线是铅直的， 上半平面为 x 轴的负方向。
进一步地， 一个带可以定义为一条线的上半平面和另一条（平行）线的下半平面的交集。
给定一个凸多边形 P ， 一个方向角 theta ， 下切线 tl(P, theta) 是一条与 x 轴正半轴夹角为 theta 的线， 他与 P相交并且 P 在 tl(P, theta) 的上半平面。 交点（可能不止一个）称为下顶点。
同样的， 定义上切线和上顶点。
给定一个家庭的多边形集合和一个固定的方向角， 就确定了一个下顶点集和上顶点集。
最后， 考虑下面的结论：
给定家庭 F 的多边形集， 和一个方向角 theta ， 一个带 S （由 Hu(l1) 和 Hl(l2) 大于0的交集得到）是 F （在此方向上）最小宽度带， 当且仅当 F 中存在两个多边形 P 和 Q 有
- P 和 Hu(l1) 的交在 l1 上。
- Q 和 Hl(l2) 的交在 l2 上。
其主要的结论是： 一个家庭 F 的凸多边形集的最小宽度带（一个给定方向 theta 上）由 l1 和 l2 确定当
l1=tl(CH(UP(F, theta)), theta) 且
l2=tu(CH(LP(F, theta)), theta) 成立。
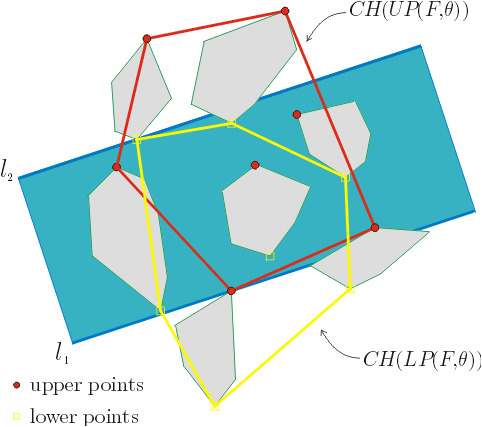一个家庭的凸多边形集， 以及给定角度上的最小带宽。 下顶点和上顶点的凸包， 上述的结论如图所示。 注意到两个多边形和带的交都只在一个顶点上出现。
因此， 只要确定了家庭多边形集的下顶点和上顶点的序列， 就能通过计算凸包得到给定方向上最小宽度带。就如Robert和Toussaint解释的， 幸运的是这些凸包不需要每次都完全重新计算： 他们需要更新即可。 实际上， 考虑两个接近的方向：许多（或者是全部）多边形对于这两个方向拥有相同的上顶点和下顶点。 这个结果同样暗示这只有有限的方向上（当下顶点或上顶点变化时）需要检测。
这里的焦点在于旋转卡壳模型， 而非关系到算法的细节。 本文打算利用旋转卡壳来计算多边形的上顶点和下顶点。下面是算法的主要实现过程。 给定一个凸多边形 P ：
- 找到拥有最小和最大 y 坐标的顶点。 标记为 p 和 q 并且通过他们构造水平切线。
- 逆时针将切线旋转过 theta 角直到其中一条与其中一个多边形的边平行。
- 如果顶点在 p 后被击出（按照逆时针方向）， 那么 p 就是对于角度0（包括）到角度 theta（不包括） 之间的下顶点。 如果顶点是在 q 后被击出， 那么 q 就是同样角度范围内的上顶点。 这两个情况当边平行的时候也可能同时发生。
- 更新当前点为新击出的顶点， 并更新当前角度。
- 重复执行步骤2到步骤4， 同时跟新角度区间， 知道新的角度大等于180度（在哪一点先回到了最初的位置， 但此时次序颠倒）。
线与其中一个多边形的一条边平行的方向称之为 临界方向 。 他们只在上顶点和下顶点处发生变化。 对于一个临界方向， 因为线穿过两个顶点， 当逆时针旋转时下顶点或是上顶点之一被定义为多边形与线的一个交点。
一旦临界方向（按照顺序给出）得到， 一个带就能在第一个方向上进行计算。 然后， 在第二个临界方向上， 至少一个上顶点或是下顶点被更新。 因此， 凸包此时需要更新， 而非重新计算一次。 一旦完成上述步骤， 新的带就构造成功了， 并且他的宽度（边界间的正交距离）被算出。 对所有临界方向重复这个操作。 注意到如果任何点处如果产生了一个宽度为0的带f， 这个过程就能够因为找到一条穿过所有家庭多边形的线而终止了。
对于完整的算法描述， 正确性讨论和运行时间分析， 见作者的论文：
J.-M. Robert, G.T. Toussaint. Computational geometry and facility location. Proc. Internatioanl Conf. on Operations Research and Management Science, Manila, The Philippines, Dec. 11-15, 1990. pp B-1 to B-19.
源自：http://cgm.cs.mcgill.ca/~orm/rotcal.frame.html