Gradient Boosted Regression
3.2.4.3.6. sklearn.ensemble.GradientBoostingRegressor
- class sklearn.ensemble. GradientBoostingRegressor ( loss='ls', learning_rate=0.1, n_estimators=100, subsample=1.0, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False ) [source]
-
Gradient Boosting for regression.
GB builds an additive model in a forward stage-wise fashion; it allows for the optimization of arbitrary differentiable loss functions. In each stage a regression tree is fit on the negative gradient of the given loss function.
Read more in the User Guide.
P
a
r
a
m
e
t
e
r
s
:
loss : {‘ls’, ‘lad’, ‘huber’, ‘quantile’}, optional (default=’ls’)
loss function to be optimized. ‘ls’ refers to least squares regression. ‘lad’ (least absolute deviation) is a highly robust loss function solely based on order information of the input variables. ‘huber’ is a combination of the two. ‘quantile’ allows quantile regression (usealpha to specify the quantile).
learning_rate : float, optional (default=0.1)
learning rate shrinks the contribution of each tree by learning_rate. There is a trade-off between learning_rate and n_estimators.
n_estimators : int (default=100)
The number of boosting stages to perform. Gradient boosting is fairly robust to over-fitting so a large number usually results in better performance.
max_depth : integer, optional (default=3)
maximum depth of the individual regression estimators. The maximum depth limits the number of nodes in the tree. Tune this parameter for best performance; the best value depends on the interaction of the input variables. Ignored if max_leaf_nodes is not None.
min_samples_split : integer, optional (default=2)
The minimum number of samples required to split an internal node.
min_samples_leaf : integer, optional (default=1)
The minimum number of samples required to be at a leaf node.
min_weight_fraction_leaf : float, optional (default=0.)
The minimum weighted fraction of the input samples required to be at a leaf node.
subsample : float, optional (default=1.0)
The fraction of samples to be used for fitting the individual base learners. If smaller than 1.0 this results in Stochastic Gradient Boosting. subsample interacts with the parametern_estimators. Choosing subsample < 1.0 leads to a reduction of variance and an increase in bias.
max_features : int, float, string or None, optional (default=None)
- The number of features to consider when looking for the best split:
-
- If int, then consider max_features features at each split.
- If float, then max_features is a percentage and int(max_features * n_features)features are considered at each split.
- If “auto”, then max_features=n_features.
- If “sqrt”, then max_features=sqrt(n_features).
- If “log2”, then max_features=log2(n_features).
- If None, then max_features=n_features.
Choosing max_features < n_features leads to a reduction of variance and an increase in bias.
Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than max_features features.
max_leaf_nodes : int or None, optional (default=None)
Grow trees with max_leaf_nodes in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.
alpha : float (default=0.9)
The alpha-quantile of the huber loss function and the quantile loss function. Only ifloss='huber' or loss='quantile'.
init : BaseEstimator, None, optional (default=None)
An estimator object that is used to compute the initial predictions. init has to provide fitand predict. If None it uses loss.init_estimator.
verbose : int, default: 0
Enable verbose output. If 1 then it prints progress and performance once in a while (the more trees the lower the frequency). If greater than 1 then it prints progress and performance for every tree.
warm_start : bool, default: False
When set to True, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just erase the previous solution.
random_state : int, RandomState instance or None, optional (default=None)
If int, random_state is the seed used by the random number generator; If RandomState instance, random_state is the random number generator; If None, the random number generator is the RandomState instance used by np.random.
A
t
t
r
i
b
u
t
e
s
:
feature_importances_ : array, shape = [n_features]
The feature importances (the higher, the more important the feature).
oob_improvement_ : array, shape = [n_estimators]
The improvement in loss (= deviance) on the out-of-bag samples relative to the previous iteration. oob_improvement_[0] is the improvement in loss of the first stage over the initestimator.
train_score_ : array, shape = [n_estimators]
The i-th score train_score_[i] is the deviance (= loss) of the model at iteration i on the in-bag sample. If subsample == 1 this is the deviance on the training data.
loss_ : LossFunction
The concrete LossFunction object.
`init` : BaseEstimator
The estimator that provides the initial predictions. Set via the init argument orloss.init_estimator.
estimators_ : ndarray of DecisionTreeRegressor, shape = [n_estimators, 1]
The collection of fitted sub-estimators.
See also
DecisionTreeRegressor, RandomForestRegressor
References
J. Friedman, Greedy Function Approximation: A Gradient Boosting Machine, The Annals of Statistics, Vol. 29, No. 5, 2001.
- Friedman, Stochastic Gradient Boosting, 1999
T. Hastie, R. Tibshirani and J. Friedman. Elements of Statistical Learning Ed. 2, Springer, 2009.
Methods
decision_function(*args, **kwargs) DEPRECATED: and will be removed in 0.19 fit(X, y[, sample_weight, monitor]) Fit the gradient boosting model. fit_transform(X[, y]) Fit to data, then transform it. get_params([deep]) Get parameters for this estimator. predict(X) Predict regression target for X. score(X, y[, sample_weight]) Returns the coefficient of determination R^2 of the prediction. set_params(**params) Set the parameters of this estimator. staged_decision_function(*args, **kwargs) DEPRECATED: and will be removed in 0.19 staged_predict(X) Predict regression target at each stage for X. transform(X[, threshold]) Reduce X to its most important features. - __init__ ( loss='ls', learning_rate=0.1, n_estimators=100, subsample=1.0, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False ) [source]
- decision_function ( *args, **kwargs ) [source]
-
DEPRECATED: and will be removed in 0.19
Compute the decision function of X.
Parameters: X : array-like of shape = [n_samples, n_features]
The input samples.
Returns: score : array, shape = [n_samples, n_classes] or [n_samples]
The decision function of the input samples. The order of the classes corresponds to that in the attribute classes_. Regression and binary classification produce an array of shape [n_samples].
- feature_importances_
-
- Return the feature importances (the higher, the more important the
- feature).
Returns: feature_importances_ : array, shape = [n_features]
- fit ( X, y, sample_weight=None, monitor=None ) [source]
-
Fit the gradient boosting model.
P
a
r
a
m
e
t
e
r
s:
X : array-like, shape = [n_samples, n_features]
Training vectors, where n_samples is the number of samples and n_features is the number of features.
y : array-like, shape = [n_samples]
Target values (integers in classification, real numbers in regression) For classification, labels must correspond to classes.
sample_weight : array-like, shape = [n_samples] or None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. In the case of classification, splits are also ignored if they would result in any single class carrying a negative weight in either child node.
monitor : callable, optional
The monitor is called after each iteration with the current iteration, a reference to the estimator and the local variables of _fit_stages as keyword arguments callable(i,self, locals()). If the callable returns True the fitting procedure is stopped. The monitor can be used for various things such as computing held-out estimates, early stopping, model introspect, and snapshoting.
R
e
t
u
r
n
s:
self : object
Returns self.
- fit_transform ( X, y=None, **fit_params ) [source] ¶
-
Fit to data, then transform it.
Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.
Parameters: X : numpy array of shape [n_samples, n_features]
Training set.
y : numpy array of shape [n_samples]
Target values.
Returns: X_new : numpy array of shape [n_samples, n_features_new]
Transformed array.
- get_params ( deep=True ) [source]
-
Get parameters for this estimator.
Parameters: deep: boolean, optional :
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
- predict ( X ) [source]
-
Predict regression target for X.
Parameters: X : array-like of shape = [n_samples, n_features]
The input samples.
Returns: y : array of shape = [n_samples]
The predicted values.
- score ( X, y, sample_weight=None ) [source]
-
Returns the coefficient of determination R^2 of the prediction.
The coefficient R^2 is defined as (1 - u/v), where u is the regression sum of squares ((y_true - y_pred) ** 2).sum() and v is the residual sum of squares ((y_true - y_true.mean()) ** 2).sum(). Best possible score is 1.0, lower values are worse.
Parameters: X : array-like, shape = (n_samples, n_features)
Test samples.
y : array-like, shape = (n_samples) or (n_samples, n_outputs)
True values for X.
sample_weight : array-like, shape = [n_samples], optional
Sample weights.
Returns: score : float
R^2 of self.predict(X) wrt. y.
- set_params ( **params ) [source]
-
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The former have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.
Returns: self :
- staged_decision_function ( *args, **kwargs ) [source]
-
DEPRECATED: and will be removed in 0.19
Compute decision function of X for each iteration.
This method allows monitoring (i.e. determine error on testing set) after each stage.
Parameters: X : array-like of shape = [n_samples, n_features]
The input samples.
Returns: score : generator of array, shape = [n_samples, k]
The decision function of the input samples. The order of the classes corresponds to that in the attribute classes_. Regression and binary classification are special cases with k == 1, otherwise k==n_classes.
- staged_predict ( X ) [source]
-
Predict regression target at each stage for X.
This method allows monitoring (i.e. determine error on testing set) after each stage.
Parameters: X : array-like of shape = [n_samples, n_features]
The input samples.
Returns: y : generator of array of shape = [n_samples]
The predicted value of the input samples.
- transform ( X, threshold=None ) [source]
-
Reduce X to its most important features.
Uses coef_ or feature_importances_ to determine the most important features. For models with a coef_ for each class, the absolute sum over the classes is used.
Parameters: X : array or scipy sparse matrix of shape [n_samples, n_features]
The input samples.
threshold : string, float or None, optional (default=None)
The threshold value to use for feature selection. Features whose importance is greater or equal are kept while the others are discarded. If “median” (resp. “mean”), then the threshold value is the median (resp. the mean) of the feature importances. A scaling factor (e.g., “1.25*mean”) may also be used. If None and if available, the object attribute threshold is used. Otherwise, “mean” is used by default.
Returns: X_r : array of shape [n_samples, n_selected_features]
The input samples with only the selected features.
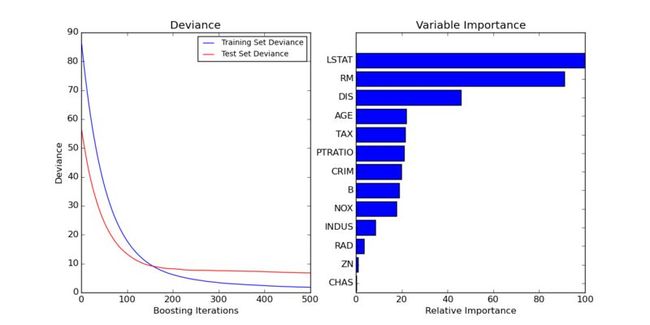
Demonstrate Gradient Boosting on the Boston housing dataset.
This example fits a Gradient Boosting model with least squares loss and 500 regression trees of depth 4.
print(__doc__) # Author: Peter Prettenhofer <[email protected]> # # License: BSD 3 clause import numpy as np import matplotlib.pyplot as plt from sklearn import ensemble from sklearn import datasets from sklearn.utils import shuffle from sklearn.metrics import mean_squared_error ############################################################################### # Load data boston = datasets.load_boston() X, y = shuffle(boston.data, boston.target, random_state=13) X = X.astype(np.float32) offset = int(X.shape[0] * 0.9) X_train, y_train = X[:offset], y[:offset] X_test, y_test = X[offset:], y[offset:] ############################################################################### # Fit regression model params = {'n_estimators': 500, 'max_depth': 4, 'min_samples_split': 1, 'learning_rate': 0.01, 'loss': 'ls'} clf = ensemble.GradientBoostingRegressor(**params) clf.fit(X_train, y_train) mse = mean_squared_error(y_test, clf.predict(X_test)) print("MSE: %.4f" % mse) ############################################################################### # Plot training deviance # compute test set deviance test_score = np.zeros((params['n_estimators'],), dtype=np.float64) for i, y_pred in enumerate(clf.staged_decision_function(X_test)): test_score[i] = clf.loss_(y_test, y_pred) plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.title('Deviance') plt.plot(np.arange(params['n_estimators']) + 1, clf.train_score_, 'b-', label='Training Set Deviance') plt.plot(np.arange(params['n_estimators']) + 1, test_score, 'r-', label='Test Set Deviance') plt.legend(loc='upper right') plt.xlabel('Boosting Iterations') plt.ylabel('Deviance') ############################################################################### # Plot feature importance feature_importance = clf.feature_importances_ # make importances relative to max importance feature_importance = 100.0 * (feature_importance / feature_importance.max()) sorted_idx = np.argsort(feature_importance) pos = np.arange(sorted_idx.shape[0]) + .5 plt.subplot(1, 2, 2) plt.barh(pos, feature_importance[sorted_idx], align='center') plt.yticks(pos, boston.feature_names[sorted_idx]) plt.xlabel('Relative Importance') plt.title('Variable Importance') plt.show()