求一个数组的最大子数组(C/C++实现)
最大子数组:要求相连,加起来的和最大的子数组就是一个数组的最大子数组。编译环境:VS2012,顺便说句其实我是C#程序员,我只是喜欢学C++。
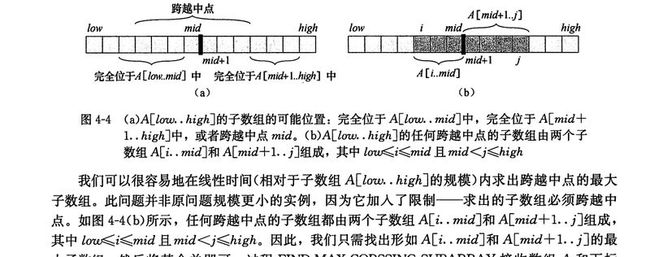
其实这是个半成品,还有些BUG在里面,不过总体的思路是这样的,求最大的子数组,由一个中位分开,就是数组的中间位置,然后分别求中间位置横跨的,左边的,和右边的最大的,然后比较三者的大小,最大的为最大子数组。思路来自算法导论。今天算是把伪代码都实现了,但是貌似有点BUG,不知道有大神帮我提一下不?为了节约时间,我索性把一些问题的解释放过来,是算法导论的,我也是看的这本书做的。
本人声明,这次是我自己写的代码,下面的,我没有看别人写的,主要还是想锻炼下自己,结合上面的算法导论看基本上就没什么问题了,晚安。
// ConsoleApplication8.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
template <class T>
int getArrayLen(T& array) //使用模板定义一个函数getArrayLen,该函数将返回数组array的长度
{
return (sizeof(array) / sizeof(array[0]));
}
int _tmain(int argc, _TCHAR* argv[])
{
void findMaxSubArray(int [],int);
int a[]={5,-100,34535,32,10,5,4,-100,2}; //初始化数组
int len=getArrayLen(a);
findMaxSubArray(a,len);
system("pause");
return 0;
}
void findMaxSubArray(int a[],int len)
{
//声明
int getSubArraysPreIterator(int [],int ,int,int );
int getSubArrayMid(int ,int ,int ,int [],int );
//低位下标
int low=0;
//高位下标
int high=0;
//中间位数
int mid=0;
//最大子数组
int sum=0; //第一种情况下
int sumAfter=0; //第二种情况下
int sumMid=0; //第三种情况下
int mid_RightPos=0; //横跨中间数组的右边界
int mid_LeftPos=0; //横跨中间的数组的左边界
int sumMidFromRight=0; //从右边开始计算
int arrLen=len;//数组长度
//如果数组中只有一个元素
if(arrLen==1)
{
cout<<" 最大子数组是:"<<a[0]<<endl;
}
mid=arrLen/2; //算出中间的位置
/*有3种可能的情况
1.最大子数组在中位数的左边
2.最大子数组在中位数的右边
3.最大子数组横跨中间*/
//先求第一种情况
for(int i=mid;i>=0;i--)
{
sum=sum+a[i];
int sum_=getSubArraysPreIterator(a,mid,i,0);
if(sum<sum_)
{
sum=getSubArraysPreIterator(a,mid,i,0);
low=i; //最大子数组左边的边界。
}
}
cout<<"最大子数组(左)是:"<<sum<<endl;
cout<<"low:"<<low<<endl;
//第二种情况
for(int i=mid+1;i<arrLen;i++)
{
sumAfter=sumAfter+a[i];
int sum_After=getSubArraysPreIterator(a,mid,i,1);
if(sumAfter<sum_After)
{
sumAfter=getSubArraysPreIterator(a,mid,i,1);
high=i;
}
//如果没进入上面的IF语句,则表示是最后一个
if(high==0&&i==arrLen-1)
{
high=i;
}
}
cout<<"最大子数组(右)是:"<<sumAfter<<endl;
cout<<"high:"<<high<<endl;
//确定了最低位的下标和最高位的下标,下面进行跨中位运算
for(int i=low+1;i<high;i++)
{
sumMid=sumMid+a[i];
//从LOW开始考虑问题
int sumMid_=getSubArrayMid(low,high,i,a,0);
if(sumMid<sumMid_)
{
sumMid=getSubArrayMid(low,high,i,a,0);
mid_RightPos=i;
}
//从HIGH开始考虑问题
int sumMid_High=getSubArrayMid(low,high,i,a,1);
if(sumMid<sumMid_High)
{
sumMidFromRight=getSubArrayMid(low,high,i,a,1);
mid_LeftPos=i;
}
//比较大小
if(sumMid<sumMidFromRight)
{
sumMid=sumMidFromRight;
mid_RightPos=mid_LeftPos;
}
}
cout<<"横跨中间的子数组是:"<<sumMid<<endl;
cout<<"横跨中间的数组的右边界是:"+mid_RightPos<<endl;
//比较三个求出来的值的大小,确定谁才是最大子数组。
if(sum>sumAfter)
{
if(sum>sumMid)
{
cout<<"最终结果:"<<sum<<"为最大子数组"<<endl;
}
else
{
cout<<"最终结果:"<<sumMid<<"为最大子数组"<<endl;
}
}
else
{
if(sum<sumMid)
{
if(sumMid>sumAfter)
{
cout<<"最终结果:"<<sumMid<<"为最大子数组"<<endl;
}
else
{
cout<<"最终结果:"<<sumAfter<<"为最大子数组"<<endl;
}
}
}
}
//根据下标获得子数组(前一次迭代的和的结果)
int getSubArraysPreIterator(int a[],int mid,int i,int flag)
{
//获得要求的子数组的跨度
int span=mid-i;
//总和
int sum=0;
//左边
if(flag==0)
{
//计算前一次元素的和,以和上面的后一次的函数所得到的和做笔记
for(int k=mid;k>=i+1;k--)
{
sum+=a[k];
}
return sum;
}
//右边
if(flag ==1)
{
for(int k=mid+1;k<i;k++)
{
sum+=a[k];
}
return sum;
}
}
//获得子数组(跨中线)
//注意:因为从中线可能是从中线的左边,或者是右边的数组是最大子数组,所以要区别对待
int getSubArrayMid(int low,int high,int i,int a[],int flag)
{
int sum=0;
if(flag==0)
{
for(int k=low+1;k<i;k++)
{
sum+=a[k];
}
return sum;
}
else if(flag==1)
{
for(int k=high-1;k>i;k--)
{
sum+=a[k];
}
return sum;
}
}