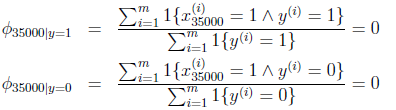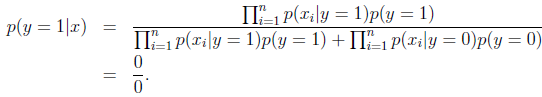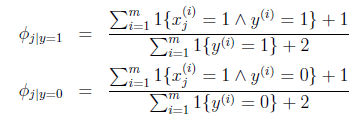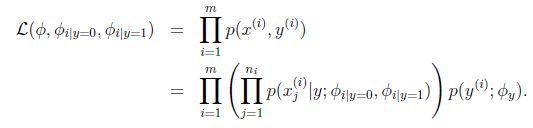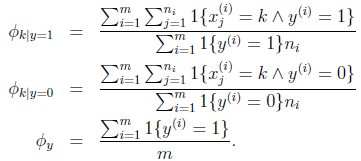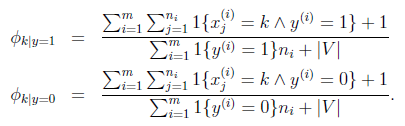高斯判别分析和朴素贝叶斯

高斯判别分析

　　对于输入数据x是连续随机变量的分类问题，我们使用高斯判别分析(Gaussian Discriminant Analysis)，使用多元正态分布来建立模型p(x|y)。

　　

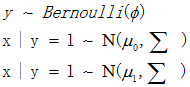
　　写出对应的分布函数：

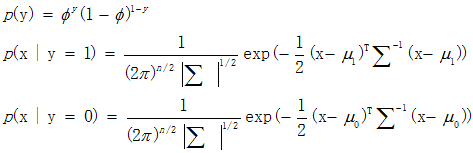
　　其中的参数是Φ,∑,μ₁,μ_0,使用最大似然估计求出参数值，在求解过程中将方程转化为对数形式能简化计算步骤。

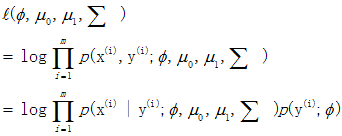
　　通过最大化处理，得出参数的最大似然估计值

　　假设输入数据x是二维的，则能画出类似于下面的分类器图形。

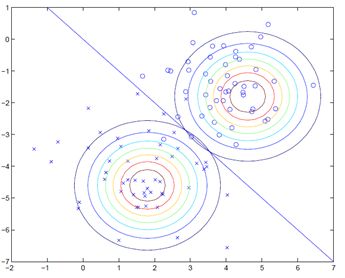
　　上图画出了两个高斯分布的等高线，由于它们的协防差相同，因此等高线的形状相同，均值的不同区分出了两类点的分布区域，直线即为分割两中类型的决策边界。

 

朴素贝叶斯算法

　　在GDA中，我们要求特征向量x是连续实数向量。如果x是离散值的话，可以考虑采用朴素贝叶斯的分类方法。假设我们有一个训练集（标有垃圾邮件和非垃圾邮件的集合），把新接收到的邮件内容填充到特征向量x中，x的维度为词汇表中英文单词的数量，例如邮件中有"buy"这个单词，则在x中把单词"buy"对应的维度的值设为1。

　　假设词汇表中有50000个单词， ，如果x使用多项分布建立模型p(x|y)，参数的数量将达到，显然所需要的参数太多，因此在朴素贝叶斯算法中，我们会提出一种假设，称作朴素贝叶斯假设(Naive Bayes (NB) assumption)对于给定的y，特征向量x中的值是条件独立的，也就是说假如有一封垃圾邮件(y=1),邮件中出现"buy"的概率与出现"price"的概率是无关的。

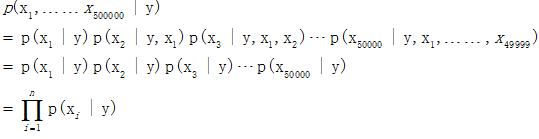
　　式子的第二个等式就是运用了朴素贝叶斯假设，接下来跟上面高斯判别分析求解最大似然估计一样，对于给定的训练集{(x⁽ⁱ⁾,y⁽ⁱ⁾)};i=1,……,m,我们写下对应的最大似然估计：

　　关于三个参数求偏导得到：

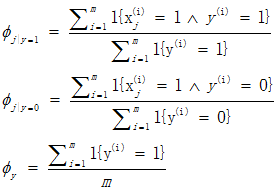
　　式中^表示与的意思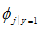，表示单词j出现的垃圾邮件的数量占总垃圾邮件数量的比值。

接着可以得出给对于给定的特征向量x，垃圾邮件出现的后验概率：

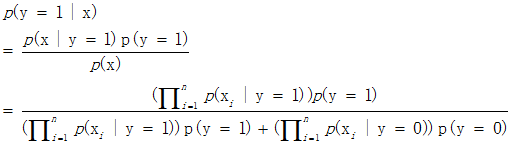
拉普拉斯平滑

　　上述的朴素贝叶斯算法有个小缺点。比如前面提到的邮件分类，现在新来了一封邮件，邮件标题是"NIPS call for papers"。我们使用更大的网络词典（词的数目由5000变为35000）来分类，假设NIPS这个词在字典中的位置是35000。然而NIPS这个词没有在训练数据中出现过，这封邮件第一次出现了NIPS。那我们算概率的时候如下：

　　由于NIPS在以前的不管是垃圾邮件还是正常邮件都没出现过，那么结果只能是0了。

　　显然最终的条件概率也是0。

　　原因就是我们的特征概率条件独立，使用的是相乘的方式来得到结果。为了解决这个问题，我们打算给未出现特征值，赋予一个"小"的值而不是0。具体平滑方法：假设离散型随机变量z有{1,2,…,k}个值，我们用来表示每个值的概率。假设有m个训练样本中，z的观察值是其中每一个观察值对应k个值中的一个。那么根据原来的估计方法可以得到

　　说白了就是z=j出现的比例。拉普拉斯平滑法将每个k值出现次数事先都加1，通俗讲就是假设他们都出现过一次。那么修改后的表达式为：

　　每个z=j的分子都加1，分母加k。可见。回到邮件分类的问题，修改后的公式为：

文本分类的事件模型

　　回想一下我们刚刚使用的用于文本分类的朴素贝叶斯模型，这个模型称作多值伯努利事件模型（multi-variate Bernoulli event model）。在这个模型中，我们首先随机选定了邮件的类型（垃圾或者普通邮件，也就是p(y)），然后一个人翻阅词典，从第一个词到最后一个词，随机决定一个词是否要在邮件中出现，出现标示为1，否则标示为0。然后将出现的词组成一封邮件。决定一个词是否出现依照概率p(xi|y)。那么这封邮件的概率可以标示为。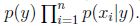

　　让我们换一个思路，这次我们不先从词典入手，而是选择从邮件入手。让i表示邮件中的第i个词，xi表示这个词在字典中的位置，那么xi取值范围为{1,2,…|V|}，|V|是字典中词的数目。这样一封邮件可以表示成，n可以变化，因为每封邮件的词的个数不同。然后我们对于每个xi随机从|V|个值中取一个，这样就形成了一封邮件。这相当于重复投掷|V|面的骰子，将观察值记录下来就形成了一封邮件。当然每个面的概率服从p(xi|y)，而且每次试验条件独立。这样我们得到的邮件概率是。居然跟上面的一样，那么不同点在哪呢？注意第一个的n是字典中的全部的词，下面这个n是邮件中的词个数。上面xi表示一个词是否出现，只有0和1两个值，两者概率和为1。下面的xi表示|V|中的一个值，|V|个p(xi|y)相加和为1。是多值二项分布模型。上面的x向量都是0/1值，下面的x的向量都是字典中的位置。

　　形式化表示为：

　　m个训练样本表示为：

　　表示第i个样本中，共有ni个词，每个词在字典中的编号为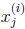。那么我们仍然按照朴素贝叶斯的方法求得最大似然估计概率为

　　解得，

　　这里如果假如拉普拉斯平滑，得到公式为：

　　表示每个k值至少发生过一次。