优化的热点分析与异常值分析:让数据分析更加便捷高效
热点分析作为一种常用的空间统计方法,能够帮助我们识别地理空间中的热点和冷点区域,即那些高值或低值集中出现的地方。而优化的热点分析进一步简化了这一过程,使用户无需手动调整参数即可获得可靠的结果。此外,异常值分析则专注于发现那些与周围区域显著不同的地点,这些异常值往往能揭示出有趣的现象或问题所在,同样的优化的异常值分析也简化了这一过程,使用户无需手动调整参数即可获得可靠的结果。
到底哪些数据需要做热点分析?
官方文档是这样说明的:优化的热点分析 (空间统计)—ArcMap | 文档 (arcgis.com)
- 计数(如街道十字路口处发生的交通事故数)
- 比率(如城市失业率,各城市以点要素表示)
- 平均值(如学校间数学测验的平均得分)
- 指数(如国家汽车经销商的消费者满意度得分)
优化的热点分析与热点分析区别在哪?
简单来说,热点分析相当于专业相机,你想拍出更美或者根据当前环境特征进行调整焦距、光圈就用热点分析,而优化的热点分析它就相当于傻瓜相机,设置都帮你调好了直接拍照就行;
优化的热点分析包括哪些默认配置?
1、初始数据评估:1.确保具有足够的加权要素可供分析(判断要素数是否是否达到 30 的标准,未达到时结果不可靠);2.评估分析字段值:最小值、最大值、平均值、标准差;3.查找位置异常值
2、通过增量空间自相关的方式寻找最佳距离,未找到基于30 个近邻的平均距离并将其用作分析范围;
3、输出结果,Gi_Bin 字段识别统计显著性热点和冷点,使用错误发现率 (FDR) 校正方法纠正了多重测试与空间依赖性。
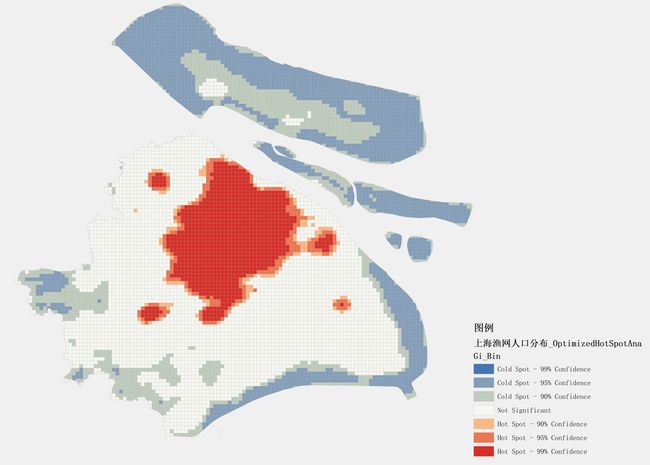
"Cold Spot - 99% Confidence"(冷点 - 99%置信度):用深蓝色表示,这类区域的人口密度相对较低,并且这一结论具有很高的可信度。
"Cold Spot - 95% Confidence"(冷点 - 95%置信度):用较浅的蓝色表示,这类区域的人口密度相对较低,并且这一结论具有较高的可信度。
"Cold Spot - 90% Confidence"(冷点 - 90%置信度):用青绿色表示,这类区域的人口密度相对较低,并且这一结论具有一定的可信度。
"Not Significant"(无显著性):用白色表示,这类区域的人口密度没有显著的高低之分。
"Hot Spot - 90% Confidence"(热点 - 90%置信度):用橙色表示,这类区域的人口密度相对较高,并且这一结论具有一定的可信度。
"Hot Spot - 95% Confidence"(热点 - 95%置信度):用较深的橙色表示,这类区域的人口密度相对较高,并且这一结论具有较高的可信度。
"Hot Spot - 99% Confidence"(热点 - 99%置信度):用红色表示,这类区域的人口密度非常高,并且这一结论具有极高的可信度。
这里边缘深蓝色的部分是未匹配出来数据的部分,前面文章也进行说明了,所以这部分可以忽略不看,结合上篇文章的结论,我们可以明显看出来上海的人口分布格局一个主城和几个周边卫星城,人口分布呈现的高高聚集特征。
从图中可以看到,上海市中心区域(红色部分)人口密度极高,这反映出上海市作为中国最大城市之一的地位。它拥有庞大的人口基数和繁荣的经济活动,使得市中心成为人口聚集的主要地点,在接近市中心的近郊地区(黄色部分),形成了多个卫星城。这些卫星城虽然人口数量相较于市中心较少,但仍然具有一定规模,它们为城市提供了重要的支持和服务功能,最外层的绿色部分代表了远郊和农村地区,这些地方人口密度最低。由于这些区域主要以农业为主导产业,因此人口规模较小且分布较散。
到底哪些数据需要做异常值分析?
官方文档是这样说明的:优化的异常值分析 (空间统计)—ArcMap | 文档 (arcgis.com)
- 研究区域中的富裕区和贫困区之间的最清晰边界在哪里?
- 研究区域中存在可以找到异常消费模式的位置吗?
- 研究区域中意想不到的糖尿病高发地在哪里?
优化的异常值分析与聚类异常值分析区别在哪?
参考''优化的热点分析与热点分析区别在哪?''的描述
优化的异常值分析包括哪些默认配置?
1、初始数据评估:1.确保具有足够的加权要素可供分析(判断要素数是否是否达到 30 的标准,未达到时结果不可靠);2.评估分析字段值:最小值、最大值、平均值、标准差;3.查找位置异常值
2、通过增量空间自相关的方式寻找最佳距离,未找到基于30 个近邻的平均距离并将其用作分析范围;
3、 输出结果,COType 字段可以识别统计显著性高低聚类(HH 和 LL)以及高低异常值(HL 和 LH),利用错误发现率 (FDR) 校正方法纠正了多重测试和空间依赖性。
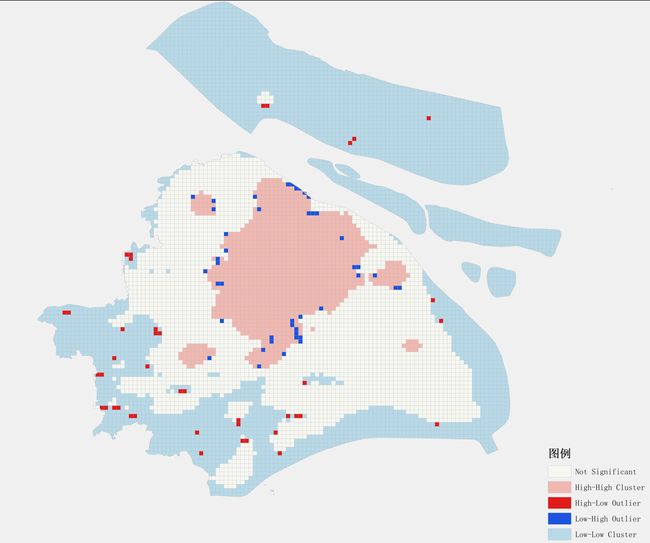
"Not Significant"(非显著):用白色表示,这类区域的变量值没有显著的聚类或离群值。
"High-High Cluster"(高-高聚类):用粉色表示,这类区域的变量值较高,并且周围邻近的区域也具有相似的高值,形成了一个高值聚类。
"High-Low Outlier"(高-低离群值):用红色表示,这类区域的变量值较高,但是周围的邻近区域却具有较低的值,形成了一种高值离群的情况。
"Low-High Outlier"(低-高离群值):用蓝色表示,这类区域的变量值较低,但是周围的邻近区域却具有较高的值,形成了一种低值离群的情况。
"Low-Low Cluster"(低-低聚类):用浅蓝色表示,这类区域的变量值较低,并且周围邻近的区域也具有相似的低值,形成了一个低值聚类。
因为是异常值分析,这里我们关注的重点在哪些地方产生了异常值,我们先来看"低-高离群值"(蓝色)是指那些具有较高人口分布的区域,但周围的邻近区域却具有较低的人口网格分布。可能的原因有很多,比如这些区域可能是公园、自然保护区或者工业区等特殊功能区,或者是尚未开发的土地,使得该区域的人口值低于周围区域。
再看一下''高-低离群值''(红色)是指那些具有较低人口分布的区域,但周围的邻近区域却具有较高的人口网格分布,可能的原因同样有很多,比如周边分布着比较集中的居民区或者宿舍区,有些地方因为历史、文化和宗教等原因,成为了特定人群聚居地或者村落等原因,使得该区域的人口值高于周围区域。
文章仅用于分享个人学习成果与个人存档之用,分享知识,如有侵权,请联系作者进行删除。所有信息均基于作者的个人理解和经验,不代表任何官方立场或权威解读。