【树】建立二叉链表存储的二叉树+遍历二叉树(先序、中序、后序、层序)
建立二叉链表存储的二叉树+遍历二叉树(先序、中序、后序、层序)
1.建立二叉链表存储的二叉树
1-1.原理
二叉树的构建利用了递归的原理,在按先序序列构建二叉树时,为了能让电脑知道每个结点是否有左右孩子,我们要对原二叉树进行扩展,明确表示每个结点的左右孩子,若当前结点没有左右孩子,我们用’#'表示。
由普通二叉树---->扩展二叉树,如下图:
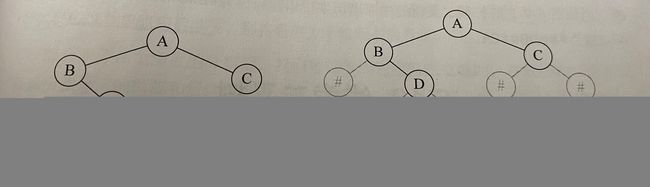
此时当我们按先序序列构建上面的二叉树时,应输入的序列为:AB#D##C##
1-2.代码
void CreateBiTree(BiTree *T) // 二叉树的构造
{
char ch;
scanf("%c", &ch);
if (ch == '#') *T = NULL; // #表示当前结点为空
else {
*T = (BiTree)malloc(sizeof(BiTNode)); // 动态申请结点内存
(*T)->data = ch; // 生成根结点
CreateBiTree(&(*T)->lchild); // 构造左子树
CreateBiTree(&(*T)->rchild); // 构造右子树
}
}
1-3.实例
#include 2.先序遍历
2-1.递归
若二叉树为空,则返回;否则先访问根结点,然后先序遍历左子树,最后先序遍历右子树。
void PreOrderTraverse(BiTree T) // 先序遍历二叉树
{
if (T == NULL) return;
printf("%c", T->data); // 先显示结点数据
PreOrderTraverse(T->lchild); // 再先序遍历左子树
PreOrderTraverse(T->rchild); // 最后先序遍历右子树
}
2-2.非递归
用栈来实现:
(1)首先访问根结点,根节点入栈并进去其左子树,然后访问左子树的根节点,入栈并进入下一层的左子树,直到当前结点为空。
(2)若栈此时非空,则从栈中退出栈顶元素,进入该结点的右子树。
重复(1)(2),直到当前结点和栈都是空的,结束。
void PreOrder(BiTree T) // 先序遍历二叉树(非递归)
{
BiTNode *s[N]; // 用结构体指针数组模拟栈
int top = 0; // 设置栈顶指针
BiTNode *p;
p = T;
while (top != 0 || p != NULL) { // 若当前结点为空结点 且 栈为空,则结束
while (p != NULL) { // 若当前结点不为空,则访问根结点,根指针入栈,进入左子树
printf("%c", p->data);
s[++top] = p;
p = p->lchild;
}
if (top != 0) { // 若栈不为空,根指针退栈,进入其右子树
p = s[top--];
p = p->rchild;
}
}
}
2-3.实例
测试输入:ab#d##c##
测试输出:abdc
#include 3.中序遍历
3-1.递归
若二叉树为空,则返回;否则先中序遍历左子树,然后访问根结点,最后中序遍历右子树。
void InOrderTraverse(BiTree T)
{
if (T == NULL) return;
InOrderTraverse(T->lchild);
printf("%c", T->data);
InOrderTraverse(T->rchild);
}
3-2.非递归
用栈实现:
(1)根结点入栈,进入其左子树,进而左子树的根结点入栈,进入下一层的左子树,直到当前结点为空。
(2)若栈不为空,从栈顶退出上一层的结点,访问此结点,并进入该结点的右子树。
重复执行(1)(2),直到当前结点和栈均为空,结束。
void InOrder(BiTree T) // 中序遍历二叉树(非递归)
{
BiTNode *s[N]; // 用结构体指针数组模拟栈
int top = 0; // 设置栈顶指针
BiTNode *p;
p = T;
while (top != 0 || p != NULL) { // 若当前结点为空结点 且 栈为空,则结束
while (p != NULL) { // 若当前结点不为空,则访问根结点,根指针入栈,进入左子树
s[++top] = p;
p = p->lchild;
}
if (top != 0) { // 若栈不为空,根指针退栈,进入其右子树
p = s[top--];
printf("%c", p->data); // 先访问完左结点之后,回到根结点,再访问根节点
p = p->rchild;
}
}
}
3-3.实例
测试输入:ab#d##c##
测试输出:bdac
#include 4.后序遍历
4-1.递归
若二叉树为空,则返回;否则先后序遍历左子树,然后访问根结点,最后后序遍历右子树。
void PostOrderTraverse(BiTree T)
{
if (T == NULL) return;
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%c", T->data);
}
4-2.非递归
同样用栈来实现:
(1)根结点入栈,进入其左子树,进而左子树的根结点入栈,进入下一层左子树,直到当前结点为空。
(2)若栈非空,如果栈顶结点p的右子树为空或者已经被访问过,则退出栈,访问p结点,并将p赋值给q,p置为空;如果栈顶结点有右子树且未被访问,则进入p的右子树。
重复执行(1)(2),直到当前结点和栈均为空,结束。
void PostOrder(BiTree T) // 后序遍历二叉树(非递归)
{
BiTNode *s[N];
int top = 0;
BiTNode *p, *q; // q存储刚刚访问过的结点,p存储当前根结点
p = T;
q = NULL;
while (p != NULL || top != 0) {
while (p != NULL) {
s[++top] = p;
p = p->lchild;
}
if (top != 0) {
p = s[top]; // 获取栈顶元素
if (p->rchild == NULL || p->rchild == q) { // 若右子树为空 或者 右子树刚刚被访问过
top--; // 栈顶元素出栈
printf("%c", p->data);
q = p;
p = NULL;
}
else {
p = p->rchild;
}
}
}
}
4-3.实例
测试输入:ab#d##c##
测试输出:dbca
#include 5.层序遍历
5-1.层序遍历代码
层序遍历用队列来实现,首先根结点入队,当队列非空时,重复执行下面两个操作:
(1)队头结点出队,访问出队结点。
(2)出队结点的非空左右孩子入队。
void LevelOrder(BiTree T) // 二叉树的层序遍历
{
BiTNode *Q[N]; // 数组模拟队列
int front = 0;
int rear = 0;
BiTNode *p;
Q[++rear] = T; // 根结点入队
while (front != rear) { // 若队列不为空
// 队头结点出队,并访问出队结点
p = Q[++front];
printf("%c", p->data);
// 出队结点的非空左右孩子依次入队
if (p->lchild != NULL) {
Q[++rear] = p->lchild;
}
if (p->rchild != NULL) {
Q[++rear] = p->rchild;
}
}
}
5-2.实例
测试输入:ab#d##c##
测试输出:abcd
#include 内容参考:
《大话数据结构》 程杰
《数据结构与算法》王曙燕
