哈尔滨2013校赛训练赛 4 解题思路

A.跑步

　　二分枚举距离，然后构图用并查集判联通数量是否大与等于N，时间复杂度是 Nlog(N),

因为所给坐标较大，注意求解距离时强制转换，防止溢出～

View Code

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

#include<algorithm>

#include<math.h>

using namespace std;



const int N = 510;

const double esp = 1e-8;

int n, m, st[N], rank[N];

double dis[N][N], Max;

#define MIN(a,b) (a)<(b)?(a):(b)

#define MAX(a,b) (a)>(b)?(a):(b)



int find( int x ){

    return (st[x]==x)? x : (st[x]=find(st[x])) ;

}

int sign( double x ){

    return (x<-esp)? -1 : (x>esp);

}



struct point{

    int x, y;

    void input(){

        scanf("%d%d", &x,&y);    

    }

}p[N];



double dist( point a, point b ){

    return sqrt( 1.0*(a.x-b.x)*(a.x-b.x) + 1.0*(a.y-b.y)*(a.y-b.y) );

}



int judge( double mid ){

    

    for(int i = 0; i < n; i++ ) st[i] = i, rank[i] = 1;

    for(int i = 0; i < n; i++ ){

        for(int j = i+1; j < n; j++){

            //if( sign( dis[i][j]-mid ) <= 0 )

            if( dis[i][j] <= mid )    

            {

                int fx = find(i), fy = find(j);

                if( fx != fy ){

                    st[fy] = fx;

                    rank[fx] += rank[fy];

                }

            }

        }

    }

    int cnt = 0;

    for(int i = 0; i < n; i++)

        if( st[i] == i )

            cnt = MAX( cnt, rank[i] );

    return cnt;

}

int main(){

    int T;

    scanf("%d",&T);

    while( T-- )

    {

        scanf("%d%d", &n,&m);

        for(int i = 0; i < n; i++)

            p[i].input();

        for(int i = 0; i < n; i++)

            for(int j = i+1; j < n; j++)

            {    

                dis[i][j] = dis[j][i] = dist( p[i], p[j] );

                Max = MAX( Max, dis[i][j] );    

            }    

        double l = 0, r = Max+1, ans = 0;

        while( (r-l) > 1e-6 ){

            double mid = (r+l)/2.;

            int tmp = judge( mid );

        //    printf("mid = %lf, tmp = %d\n", mid, tmp );



            if( tmp >= m ){

                ans = r = mid;

            }

            else

                l = mid;

        }

        printf("%.4lf\n", ans );    

    }

    return 0;

}

 

B.连线

　　最小权值匹配. 只会最大匹配的匈牙利算法。去研究研究权值匹配再来写。。。

 

C.回文串

　　插值取模，使用树状数组来维护，经典字符串题

View Code

 #include<stdio.h>

 #include<stdlib.h>

 #include<string.h>

 #include<math.h>

 #include<iostream>

 using namespace std;

 

 typedef unsigned long long LL;

 const int N = 1000007;

 

 LL bit[N], C[2][N];

 int n, m;

 char str[N];

 void update( int x, LL val, int flag )

 {

     for( ; x <= n; x += x&(-x) )

         C[flag][x] += val;

 }

 LL sum( int x, int flag )

 {

     LL res = 0;

     for( ; x >= 1; x -= x&(-x) )

         res += C[flag][x];

     return res;

 }

 void InitBit(){

     bit[0] = 1;

     for(int i = 1; i < N; i++)

         bit[i] = bit[i-1]*27;

 }

 void init(){

     n = strlen( str );

     memset( C, 0, sizeof(C) );

     for(int i = 1; i <= n; i++)

     {

         int j = (n+1)-i;    

         update( i, (str[i-1]-'a'+1)*bit[i-1], 0 );

         update( j, (str[i-1]-'a'+1)*bit[j-1], 1 ); 

     }

 }

  

 void solve(){

     scanf("%d", &m);

     char op[2], ch[2]; 

     int a, b, c, d;

     while( m-- )

     {

         scanf("%s", op);

         if( op[0] == 'Q' )

         {

             scanf("%d%d",&a,&b);

             if(a > b) swap(a,b);    

             d = (n+1)-a; c = (n+1)-b;

             LL hash0 = ( sum(b,0)-sum(a-1,0) )*bit[c-1];//对阶    

             LL hash1 = ( sum(d,1)-sum(c-1,1) )*bit[a-1];    

             puts( (hash0 == hash1) ? "yes" : "no" );    

         }

         else

         {

             scanf("%d%s",&a,ch);

             b = (n+1)-a;

             update( a, (ch[0]-str[a-1])*bit[a-1], 0 );

             update( b, (ch[0]-str[a-1])*bit[b-1], 1 );

             str[a-1] = ch[0];    

         }

     }

 }

 int main(){

     InitBit();    

     int T;

     scanf("%d", &T);

     while( T-- )

     {

         scanf("%s", str ); 

         init();

         solve();

     }

     return 0;

 }

 

D.数列

　　将 b1,b2,...,bn分解素因子,化成 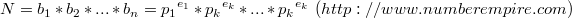 形式.

　　总共有 K 种不同的 素因子

　　令, 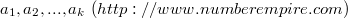 表示 第i 种素因子的次数.

　　则, 我们可以先分开考虑第 i 种素数,其共有m个,将其放置在 n个盒子中,其中盒子不同,可以为空.

　　这里有一个 组合数学关于 球放置于盒子的 问题.    具体可参考 jian1573博客 (http://www.cnblogs.com/jian1573/archive/2011/09/18/2180433.html) 

　　其方案数为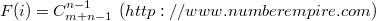

　　因为总共有 K 种 不同素数, 则总方案数为:

　　　　

　　此时问题,还没有被完全解决, 因为, 题目要求 ai > 1, 意味着, 任意个盒子,不可同时都为空, 

　　而我们上面的计算,是先假设其可以为空的情形.所以,我们需要减去所有为空的情况,剩下的才是我们的最终结果.

　　这里通过 假设,至少1个盒子为空, 至少2个盒子为空, ...,至少 n-1个盒子为空( 必定有1个盒子不为空,所以不能取到n )

　　使用容斥原理来计算.   关键点

　　　　一, 假设 1个盒子必定为空, 我们可以通过 假定盒子总数量为 n-1 个, 公式转换成 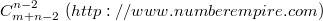  得出. 多个盒子为空同上.

　　　　二, 假设 1个盒子必定为空, 对于剩下的 n-1个盒子, 因为我们计算的是组合情形, 其中还是会出现其它盒子为空.意味着

有重复的情形. 所以这里需要用到容斥原理,  另外这里因为是 集合的并,   容斥的计算是 减奇加偶.

View Code

#include<cstdio>

#include<cstring>

#include<cstdlib>

#include<algorithm>

#include<map>

#include<cmath>

using namespace std;

typedef long long LL;



const int mod = 1e9+7;



int b[21], a[1010], n, tot;

LL C[21][21];



map<int,int>mp;



void init(){

    for(int i = 0; i <= 20; i++)

        C[i][0] = 1, C[i][i] = 1;

    for(int i = 2; i <= 20; i++)

        for(int j = 1; j < i; j++)

            C[i][j] = (C[i-1][j-1]+C[i-1][j])%mod;

}



void deal(){

    mp.clear();

    for(int i = 0; i < n; i++){

        

        int tmp_max = (int)sqrt(1.*b[i]);

        int t = b[i];

        for(int j = 2; j <= tmp_max; j++)

        {

            if( t%j == 0 ){

                if( mp.count(j) == 0 ) mp[j] = 0;



                int cnt = 0;    

                while( t%j == 0 ) (t/=j), cnt++;

                mp[j] += cnt;

            } 

        }

        if( t > 1 ){

            if( mp.count(t) == 0 ) mp[t] = 1;

            else    mp[t]++;

        }    

    }

    int idx = 0;    

    memset( a, 0, sizeof(a));

    for( map<int,int>::iterator it = mp.begin(); it != mp.end(); it++ )

        a[idx++] = it->second;

    tot = mp.size();

    

    //printf("tot = %d\n", tot );

    //for(int i = 0; i < tot; i++)

    //    printf("%d ", a[i] );

    //printf("\n\n\n");

}

void solve(){

    LL ans = 0;

        

    for(int i = 0; i < n; i++){

        LL tmp = 1;

        for(int j = 0; j < tot; j++){

            tmp = tmp*C[ n-1-i+a[j] ][ n-1-i ]%mod;    

        }

        tmp = tmp*C[n][i]%mod;

        

        if( i&1 ) tmp = -tmp;

        ans = (ans+tmp+mod)%mod;

    }

    printf("%lld\n", ans );

}

int main(){

    init();

    int T;

    scanf("%d", &T);

    while( T-- ){

        scanf("%d", &n);

        for(int i = 0; i < n; i++)

            scanf("%d", &b[i] );

        deal();    

        solve();    

    }

    return 0;

}

 

　　

　　 

E. 树形DP

    分析过程详见：http://www.cnblogs.com/yefeng1627/archive/2013/03/28/2987344.html

 

F. 最大连续和

　　线段树节点信息为{ 前缀和，后缀和，区间最大和 }， 线段树的另一类用法

　　分析过程及代码实现详见链接： http://www.cnblogs.com/yefeng1627/archive/2013/03/27/2984787.html 

  

 

G 石子游戏

　　博弈论, 简单的SG函数,但是这里最多取一半,所以对于奇数可以去 n/2+1, 偶数可以取 n/2， 对于奇异局势

的判定还是一样，若异或为0则当前为必败点。

 

H 预处理x,y和，后凸包枚举边，构直线。

　　因为点(x,y)到直线的距离计算公式为 

　　所有点到 直线 L的距离和为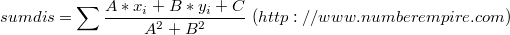  

　　然后做 凸包来枚举所有边, 就能够 O(1) 时间求出 其它点到直线的距离之和.

　　总时间复杂为 O(N)

 

I 二维最短路，dis[N][K],表示第i个城市获取k*10的金币最小花费，当J >= K 合并到 J中去。

     　一直TLE。。。想到解决方案了再来修正。。。

View Code

#include<stdio.h>

#include<string.h>

#include<stdlib.h>

#include<algorithm>

#include<vector> 

#include<queue> 

using namespace std;



const int N = 5010;

const int M = 100010;

const int INF = 0x3fffffff;

 

vector< pair<int,int> > edge[N]; 

int S, T, K;

int n, m; 

int dis[N][510];

bool vis[N];

 

queue<int> Q;

 

void spfa(){

    while(!Q.empty()) Q.pop();

    

    for(int i = 1; i <= n; i++ ){ 

        vis[i] = 0; 

        for(int j = 0; j <= K; j++)

            dis[i][j] = INF; 

    } 

    dis[S][0] = 0;

    Q.push( S );

    vis[S] = 1;

    while( !Q.empty() ){

        int u = Q.front(); Q.pop();

        vis[u] = 0;

        for(int i = 0; i < edge[u].size(); i++){

            int v = edge[u][i].first, cost = edge[u][i].second;

            for(int j = 1; j <= K; j++){

                if( dis[v][j] > dis[u][j-1]+cost ){  

                        dis[v][j] = dis[u][j-1]+cost;

                        if( !vis[v] ) Q.push(v), vis[v] = 1; 

                }     

                if(  (j==K) && (dis[v][j] > dis[u][j]+cost) ){ 

                        dis[v][j] = dis[u][j]+cost;

                        if( !vis[v] ) Q.push(v), vis[v] = 1;     

                } 

            } 

        }    

    }  

} 



int main(){

    

    int T;

    scanf("%d", &T);

    while( T-- ){

        scanf("%d%d", &n, &m);

        int a, b, c;

        for(int i = 1; i <= n; i++) edge[i].clear(); 

        for(int i = 0; i < m; i++){

            scanf("%d%d%d", &a,&b,&c);

            edge[a].push_back( make_pair(b,c) );

            edge[b].push_back( make_pair(a,c) );    

        }

        scanf("%d%d%d", &S,&T,&K);

        K = (K+9)/10;

        spfa();         

        if( dis[T][K] == INF ) puts("-1");

        else    printf("%d\n", dis[T][K] ); 

    } 

    return 0;    

} 

 

 

J 数论中的异或

　　若我们只考虑二进制表示，则每个数只有30位，对于异或操作，只能得出 1,0.   1,0的总数是对应的，

所以我们可以通过每个位置0,1数量来判定当前位置应该为0，还是1，然后化成10进制即可。